RL in Markov Games with Independent Function Approximation: Improved Sample Complexity Bound under the Local Access Model

Efficiently learning equilibria with large state and action spaces in general-sum Markov games while overcoming the curse of multi-agency is a challenging problem. Recent works have attempted to solve this problem by employing independent linear function classes to approximate the marginal $Q$-value for each agent. However, existing sample complexity bounds under such a framework have a suboptimal dependency on the desired accuracy $\varepsilon$ or the action space. In this work, we introduce a new algorithm, Lin-Confident-FTRL, for learning coarse correlated equilibria (CCE) with local access to the simulator, i.e., one can interact with the underlying environment on the visited states. Up to a logarithmic dependence on the size of the state space, Lin-Confident-FTRL learns $\epsilon$-CCE with a provable optimal accuracy bound $O(\epsilon^{-2})$ and gets rids of the linear dependency on the action space, while scaling polynomially with relevant problem parameters (such as the number of agents and time horizon). Moreover, our analysis of Linear-Confident-FTRL generalizes the virtual policy iteration technique in the single-agent local planning literature, which yields a new computationally efficient algorithm with a tighter sample complexity bound when assuming random access to the simulator.

Online Tensor Learning: Computational and Statistical Trade-offs, Adaptivity and Optimal Regret

We investigate a generalized framework for estimating latent low-rank tensors in an online setting, encompassing both linear and generalized linear models. This framework offers a flexible approach for handling continuous or categorical variables. Additionally, we investigate two specific applications: online tensor completion and online binary tensor learning. To address these challenges, we propose the online Riemannian gradient descent algorithm, which demonstrates linear convergence and the ability to recover the low-rank component under appropriate conditions in all applications. Furthermore, we establish a precise entry-wise error bound for online tensor completion. Notably, our work represents the first attempt to incorporate noise in the online low-rank tensor recovery task. Intriguingly, we observe a surprising trade-off between computational and statistical aspects in the presence of noise. Increasing the step size accelerates convergence but leads to higher statistical error, whereas a smaller step size yields a statistically optimal estimator at the expense of slower convergence. Moreover, we conduct regret analysis for online tensor regression. Under the fixed step size regime, a fascinating trilemma concerning the convergence rate, statistical error rate, and regret is observed. With an optimal choice of step size we achieve an optimal regret of $O(\sqrt{T})$. Furthermore, we extend our analysis to the adaptive setting where the horizon T is unknown. In this case, we demonstrate that by employing different step sizes, we can attain a statistically optimal error rate along with a regret of $O(\log T)$. To validate our theoretical claims, we provide numerical results that corroborate our findings and support our assertions.

Computationally Efficient and Statistically Optimal Robust High-Dimensional Linear Regression

High-dimensional linear regression under heavy-tailed noise or outlier corruption is challenging, both computationally and statistically. Convex approaches have been proven statistically optimal but suffer from high computational costs, especially since the robust loss functions are usually non-smooth. More recently, computationally fast non-convex approaches via sub-gradient descent are proposed, which, unfortunately, fail to deliver a statistically consistent estimator even under sub-Gaussian noise. In this paper, we introduce a projected sub-gradient descent algorithm for both the sparse linear regression and low-rank linear regression problems. The algorithm is not only computationally efficient with linear convergence but also statistically optimal, be the noise Gaussian or heavy-tailed with a finite 1 + epsilon moment. The convergence theory is established for a general framework and its specific applications to absolute loss, Huber loss and quantile loss are investigated. Compared with existing non-convex methods, ours reveals a surprising phenomenon of two-phase convergence. In phase one, the algorithm behaves as in typical non-smooth optimization that requires gradually decaying stepsizes. However, phase one only delivers a statistically sub-optimal estimator, which is already observed in the existing literature. Interestingly, during phase two, the algorithm converges linearly as if minimizing a smooth and strongly convex objective function, and thus a constant stepsize suffices. Underlying the phase-two convergence is the smoothing effect of random noise to the non-smooth robust losses in an area close but not too close to the truth. Numerical simulations confirm our theoretical discovery and showcase the superiority of our algorithm over prior methods.

Computationally Efficient and Statistically Optimal Robust Low-rank Matrix Estimation

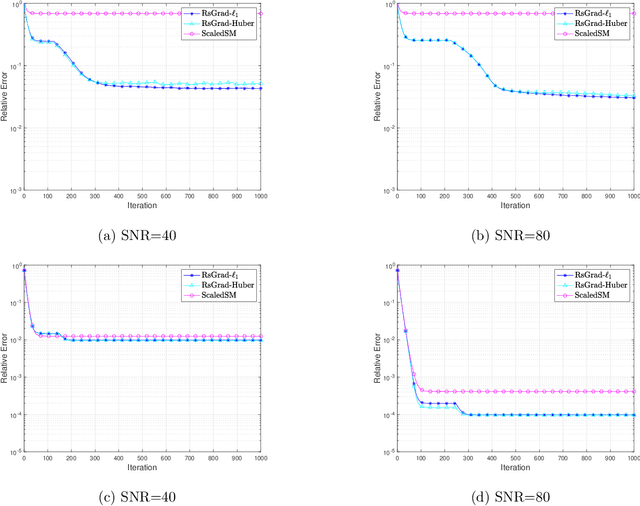
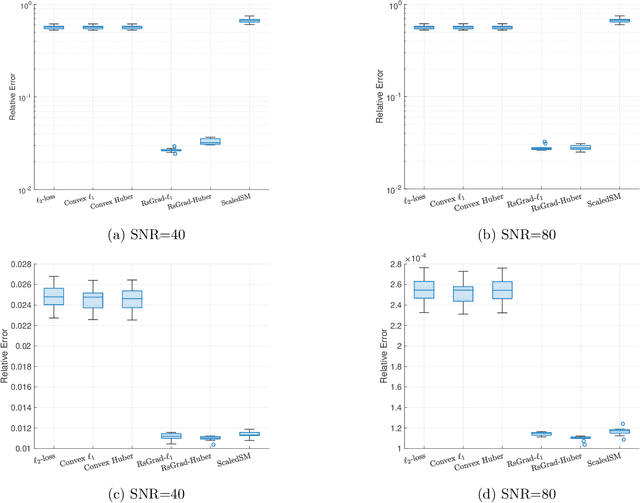
Low-rank matrix estimation under heavy-tailed noise is challenging, both computationally and statistically. Convex approaches have been proven statistically optimal but suffer from high computational costs, especially since robust loss functions are usually non-smooth. More recently, computationally fast non-convex approaches via sub-gradient descent are proposed, which, unfortunately, fail to deliver a statistically consistent estimator even under sub-Gaussian noise. In this paper, we introduce a novel Riemannian sub-gradient (RsGrad) algorithm which is not only computationally efficient with linear convergence but also is statistically optimal, be the noise Gaussian or heavy-tailed. Convergence theory is established for a general framework and specific applications to absolute loss, Huber loss and quantile loss are investigated. Compared with existing non-convex methods, ours reveals a surprising phenomenon of dual-phase convergence. In phase one, RsGrad behaves as in a typical non-smooth optimization that requires gradually decaying stepsizes. However, phase one only delivers a statistically sub-optimal estimator which is already observed in existing literature. Interestingly, during phase two, RsGrad converges linearly as if minimizing a smooth and strongly convex objective function and thus a constant stepsize suffices. Underlying the phase-two convergence is the smoothing effect of random noise to the non-smooth robust losses in an area close but not too close to the truth. Numerical simulations confirm our theoretical discovery and showcase the superiority of RsGrad over prior methods.

Fast Projected Newton-like Method for Precision Matrix Estimation with Nonnegative Partial Correlations

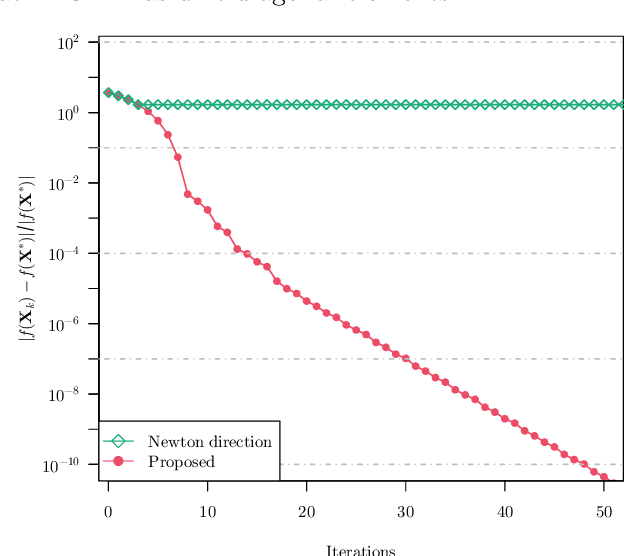
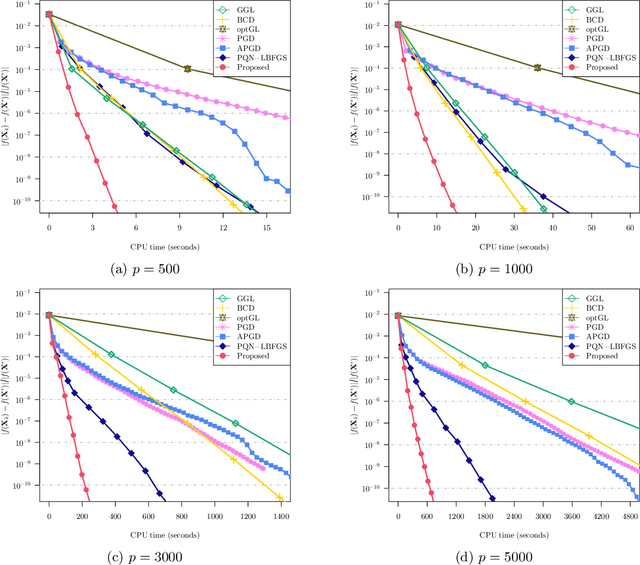
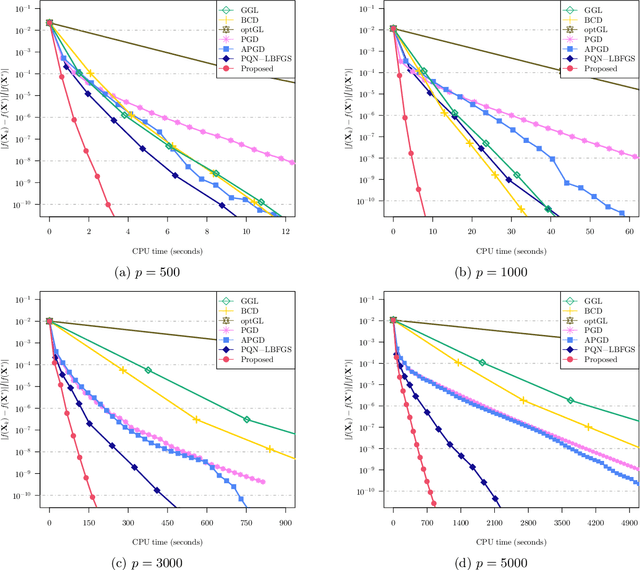
We study the problem of estimating precision matrices in multivariate Gaussian distributions where all partial correlations are nonnegative, also known as multivariate totally positive of order two ($\mathrm{MTP}_2$). Such models have received significant attention in recent years, primarily due to interesting properties, e.g., the maximum likelihood estimator exists with as few as two observations regardless of the underlying dimension. We formulate this problem as a weighted $\ell_1$-norm regularized Gaussian maximum likelihood estimation under $\mathrm{MTP}_2$ constraints. On this direction, we propose a novel projected Newton-like algorithm that incorporates a well-designed approximate Newton direction, which results in our algorithm having the same orders of computation and memory costs as those of first-order methods. We prove that the proposed projected Newton-like algorithm converges to the minimizer of the problem. We further show, both theoretically and experimentally, that the minimizer of our formulation using the weighted $\ell_1$-norm is able to recover the support of the underlying precision matrix correctly without requiring the incoherence condition present in $\ell_1$-norm based methods. Experiments involving synthetic and real-world data demonstrate that our proposed algorithm is significantly more efficient, from a computational time perspective, than the state-of-the-art methods. Finally, we apply our method in financial time-series data, which are well-known for displaying positive dependencies, where we observe a significant performance in terms of modularity value on the learned financial networks.

Provable Tensor-Train Format Tensor Completion by Riemannian Optimization

The tensor train (TT) format enjoys appealing advantages in handling structural high-order tensors. The recent decade has witnessed the wide applications of TT-format tensors from diverse disciplines, among which tensor completion has drawn considerable attention. Numerous fast algorithms, including the Riemannian gradient descent (RGrad) algorithm, have been proposed for the TT-format tensor completion. However, the theoretical guarantees of these algorithms are largely missing or sub-optimal, partly due to the complicated and recursive algebraic operations in TT-format decomposition. Moreover, existing results established for the tensors of other formats, for example, Tucker and CP, are inapplicable because the algorithms treating TT-format tensors are substantially different and more involved. In this paper, we provide, to our best knowledge, the first theoretical guarantees of the convergence of RGrad algorithm for TT-format tensor completion, under a nearly optimal sample size condition. The RGrad algorithm converges linearly with a constant contraction rate that is free of tensor condition number without the necessity of re-conditioning. We also propose a novel approach, referred to as the sequential second-order moment method, to attain a warm initialization under a similar sample size requirement. As a byproduct, our result even significantly refines the prior investigation of RGrad algorithm for matrix completion. Numerical experiments confirm our theoretical discovery and showcase the computational speedup gained by the TT-format decomposition.

Fast and Robust Spectrally Sparse Signal Recovery: A Provable Non-Convex Approach via Robust Low-Rank Hankel Matrix Reconstruction

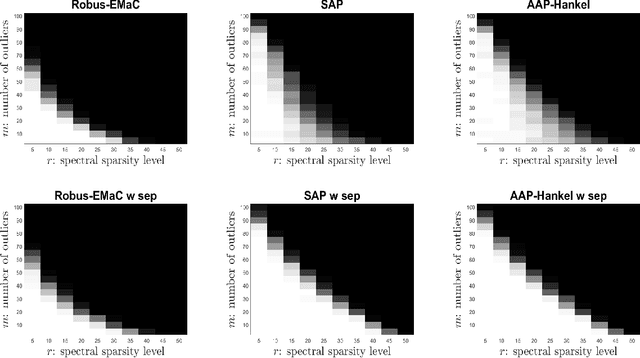
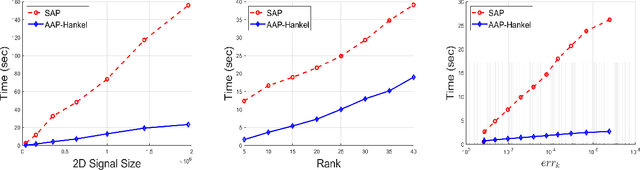
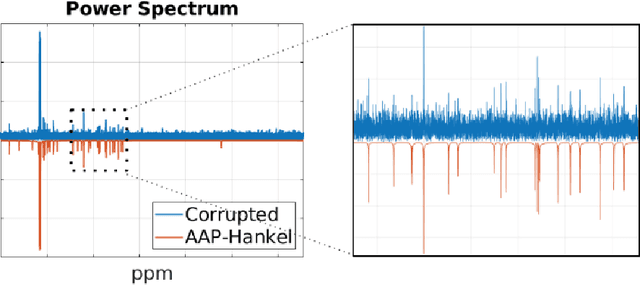
Consider a spectrally sparse signal $\boldsymbol{x}$ that consists of $r$ complex sinusoids with or without damping. We study the robust recovery problem for the spectrally sparse signal under the fully observed setting, which is about recovering $\boldsymbol{x}$ and a sparse corruption vector $\boldsymbol{s}$ from their sum $\boldsymbol{z}=\boldsymbol{x}+\boldsymbol{s}$. In this paper, we exploit the low-rank property of the Hankel matrix constructed from $\boldsymbol{x}$, and develop an efficient non-convex algorithm, coined Accelerated Alternating Projections for Robust Low-Rank Hankel Matrix Reconstruction (AAP-Hankel). The high computational efficiency and low space complexity of AAP-Hankel are achieved by fast computations involving structured matrices, and a subspace projection method for accelerated low-rank approximation. Theoretical recovery guarantee with a linear convergence rate has been established for AAP-Hankel. Empirical performance comparisons on synthetic and real-world datasets demonstrate the computational advantages of AAP-Hankel, in both efficiency and robustness aspects.

Optimal low rank tensor recovery

We investigate the sample size requirement for exact recovery of a high order tensor of low rank from a subset of its entries. In the Tucker decomposition framework, we show that the Riemannian optimization algorithm with initial value obtained from a spectral method can reconstruct a tensor of size $n\times n \times\cdots \times n$ tensor of ranks $(r,\cdots,r)$ with high probability from as few as $O((r^d+dnr)\log(d))$ entries. In the case of order 3 tensor, the entries can be asymptotically as few as $O(nr)$ for a low rank large tensor. We show the theoretical guarantee condition for the recovery. The analysis relies on the tensor restricted isometry property (tensor RIP) and the curvature of the low rank tensor manifold. Our algorithm is computationally efficient and easy to implement. Numerical results verify that the algorithms are able to recover a low rank tensor from minimum number of measurements. The experiments on hyperspectral images recovery also show that our algorithm is capable of real world signal processing problems.

Fast Single Image Reflection Suppression via Convex Optimization

Removing undesired reflections from images taken through the glass is of great importance in computer vision. It serves as a means to enhance the image quality for aesthetic purposes as well as to preprocess images in machine learning and pattern recognition applications. We propose a convex model to suppress the reflection from a single input image. Our model implies a partial differential equation with gradient thresholding, which is solved efficiently using Discrete Cosine Transform. Extensive experiments on synthetic and real-world images demonstrate that our approach achieves desirable reflection suppression results and dramatically reduces the execution time compared to the state of the art.

Enhanced Expressive Power and Fast Training of Neural Networks by Random Projections

Random projections are able to perform dimension reduction efficiently for datasets with nonlinear low-dimensional structures. One well-known example is that random matrices embed sparse vectors into a low-dimensional subspace nearly isometrically, known as the restricted isometric property in compressed sensing. In this paper, we explore some applications of random projections in deep neural networks. We provide the expressive power of fully connected neural networks when the input data are sparse vectors or form a low-dimensional smooth manifold. We prove that the number of neurons required for approximating a Lipschitz function with a prescribed precision depends on the sparsity or the dimension of the manifold and weakly on the dimension of the input vector. The key in our proof is that random projections embed stably the set of sparse vectors or a low-dimensional smooth manifold into a low-dimensional subspace. Based on this fact, we also propose some new neural network models, where at each layer the input is first projected onto a low-dimensional subspace by a random projection and then the standard linear connection and non-linear activation are applied. In this way, the number of parameters in neural networks is significantly reduced, and therefore the training of neural networks can be accelerated without too much performance loss.