JSQA: Speech Quality Assessment with Perceptually-Inspired Contrastive Pretraining Based on JND Audio Pairs

Speech quality assessment (SQA) is often used to learn a mapping from a high-dimensional input space to a scalar that represents the mean opinion score (MOS) of the perceptual speech quality. Learning such a mapping is challenging for many reasons, but largely because MOS exhibits high levels of inherent variance due to perceptual and experimental-design differences. Many solutions have been proposed, but many approaches do not properly incorporate perceptual factors into their learning algorithms (beyond the MOS label), which could lead to unsatisfactory results. To this end, we propose JSQA, a two-stage framework that pretrains an audio encoder using perceptually-guided contrastive learning on just noticeable difference (JND) pairs, followed by fine-tuning for MOS prediction. We first generate pairs of audio data within JND levels, which are then used to pretrain an encoder to leverage perceptual quality similarity information and map it into an embedding space. The JND pairs come from clean LibriSpeech utterances that are mixed with background noise from CHiME-3, at different signal-to-noise ratios (SNRs). The encoder is later fine-tuned with audio samples from the NISQA dataset for MOS prediction. Experimental results suggest that perceptually-inspired contrastive pretraining significantly improves the model performance evaluated by various metrics when compared against the same network trained from scratch without pretraining. These findings suggest that incorporating perceptual factors into pretraining greatly contributes to the improvement in performance for SQA.

Development of Interactive Nomograms for Predicting Short-Term Survival in ICU Patients with Aplastic Anemia

Aplastic anemia is a rare, life-threatening hematologic disorder characterized by pancytopenia and bone marrow failure. ICU admission in these patients often signals critical complications or disease progression, making early risk assessment crucial for clinical decision-making and resource allocation. In this study, we used the MIMIC-IV database to identify ICU patients diagnosed with aplastic anemia and extracted clinical features from five domains: demographics, synthetic indicators, laboratory results, comorbidities, and medications. Over 400 variables were reduced to seven key predictors through machine learning-based feature selection. Logistic regression and Cox regression models were constructed to predict 7-, 14-, and 28-day mortality, and their performance was evaluated using AUROC. External validation was conducted using the eICU Collaborative Research Database to assess model generalizability. Among 1,662 included patients, the logistic regression model demonstrated superior performance, with AUROC values of 0.8227, 0.8311, and 0.8298 for 7-, 14-, and 28-day mortality, respectively, compared to the Cox model. External validation yielded AUROCs of 0.7391, 0.7119, and 0.7093. Interactive nomograms were developed based on the logistic regression model to visually estimate individual patient risk. In conclusion, we identified a concise set of seven predictors, led by APS III, to build validated and generalizable nomograms that accurately estimate short-term mortality in ICU patients with aplastic anemia. These tools may aid clinicians in personalized risk stratification and decision-making at the point of care.

XGBoost-Based Prediction of ICU Mortality in Sepsis-Associated Acute Kidney Injury Patients Using MIMIC-IV Database with Validation from eICU Database

Background: Sepsis-Associated Acute Kidney Injury (SA-AKI) leads to high mortality in intensive care. This study develops machine learning models using the Medical Information Mart for Intensive Care IV (MIMIC-IV) database to predict Intensive Care Unit (ICU) mortality in SA-AKI patients. External validation is conducted using the eICU Collaborative Research Database. Methods: For 9,474 identified SA-AKI patients in MIMIC-IV, key features like lab results, vital signs, and comorbidities were selected using Variance Inflation Factor (VIF), Recursive Feature Elimination (RFE), and expert input, narrowing to 24 predictive variables. An Extreme Gradient Boosting (XGBoost) model was built for in-hospital mortality prediction, with hyperparameters optimized using GridSearch. Model interpretability was enhanced with SHapley Additive exPlanations (SHAP) and Local Interpretable Model-agnostic Explanations (LIME). External validation was conducted using the eICU database. Results: The proposed XGBoost model achieved an internal Area Under the Receiver Operating Characteristic curve (AUROC) of 0.878 (95% Confidence Interval: 0.859-0.897). SHAP identified Sequential Organ Failure Assessment (SOFA), serum lactate, and respiratory rate as key mortality predictors. LIME highlighted serum lactate, Acute Physiology and Chronic Health Evaluation II (APACHE II) score, total urine output, and serum calcium as critical features. Conclusions: The integration of advanced techniques with the XGBoost algorithm yielded a highly accurate and interpretable model for predicting SA-AKI mortality across diverse populations. It supports early identification of high-risk patients, enhancing clinical decision-making in intensive care. Future work needs to focus on enhancing adaptability, versatility, and real-world applications.

Machine Learning-Based Prediction of ICU Readmissions in Intracerebral Hemorrhage Patients: Insights from the MIMIC Databases

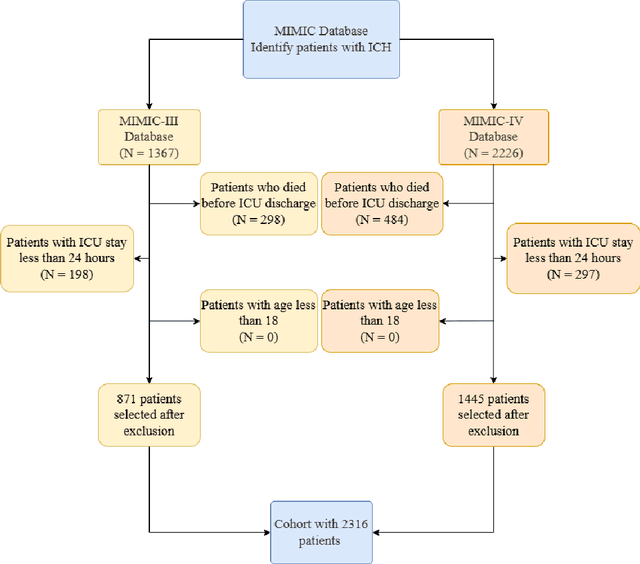
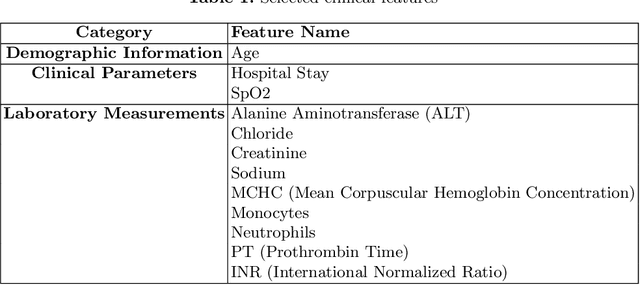
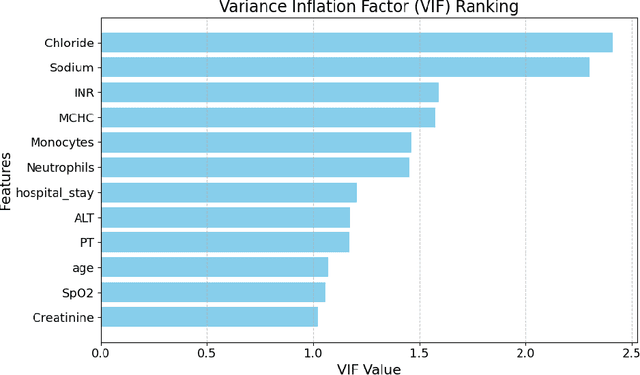
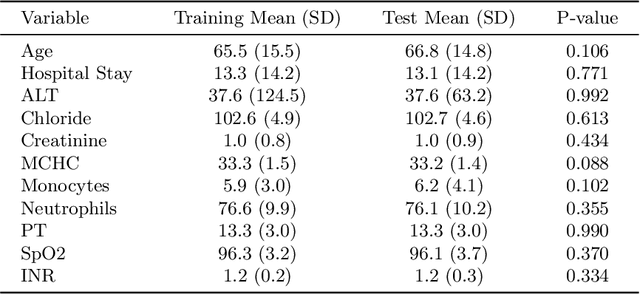
Intracerebral hemorrhage (ICH) is a life-risking condition characterized by bleeding within the brain parenchyma. ICU readmission in ICH patients is a critical outcome, reflecting both clinical severity and resource utilization. Accurate prediction of ICU readmission risk is crucial for guiding clinical decision-making and optimizing healthcare resources. This study utilized the Medical Information Mart for Intensive Care (MIMIC-III and MIMIC-IV) databases, which contain comprehensive clinical and demographic data on ICU patients. Patients with ICH were identified from both databases. Various clinical, laboratory, and demographic features were extracted for analysis based on both overview literature and experts' opinions. Preprocessing methods like imputing and sampling were applied to improve the performance of our models. Machine learning techniques, such as Artificial Neural Network (ANN), XGBoost, and Random Forest, were employed to develop predictive models for ICU readmission risk. Model performance was evaluated using metrics such as AUROC, accuracy, sensitivity, and specificity. The developed models demonstrated robust predictive accuracy for ICU readmission in ICH patients, with key predictors including demographic information, clinical parameters, and laboratory measurements. Our study provides a predictive framework for ICU readmission risk in ICH patients, which can aid in clinical decision-making and improve resource allocation in intensive care settings.

RL in Markov Games with Independent Function Approximation: Improved Sample Complexity Bound under the Local Access Model

Efficiently learning equilibria with large state and action spaces in general-sum Markov games while overcoming the curse of multi-agency is a challenging problem. Recent works have attempted to solve this problem by employing independent linear function classes to approximate the marginal $Q$-value for each agent. However, existing sample complexity bounds under such a framework have a suboptimal dependency on the desired accuracy $\varepsilon$ or the action space. In this work, we introduce a new algorithm, Lin-Confident-FTRL, for learning coarse correlated equilibria (CCE) with local access to the simulator, i.e., one can interact with the underlying environment on the visited states. Up to a logarithmic dependence on the size of the state space, Lin-Confident-FTRL learns $\epsilon$-CCE with a provable optimal accuracy bound $O(\epsilon^{-2})$ and gets rids of the linear dependency on the action space, while scaling polynomially with relevant problem parameters (such as the number of agents and time horizon). Moreover, our analysis of Linear-Confident-FTRL generalizes the virtual policy iteration technique in the single-agent local planning literature, which yields a new computationally efficient algorithm with a tighter sample complexity bound when assuming random access to the simulator.