Guojian Yin
Fast and Robust Spectrally Sparse Signal Recovery: A Provable Non-Convex Approach via Robust Low-Rank Hankel Matrix Reconstruction
Oct 13, 2019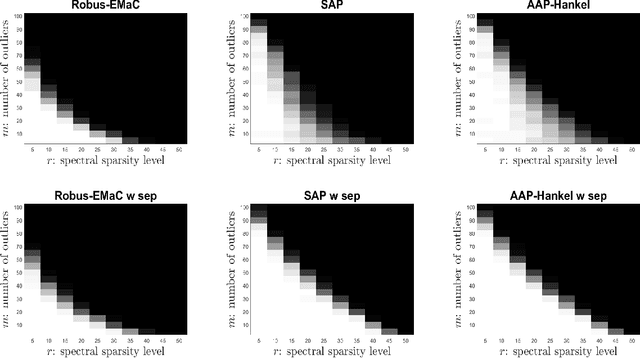
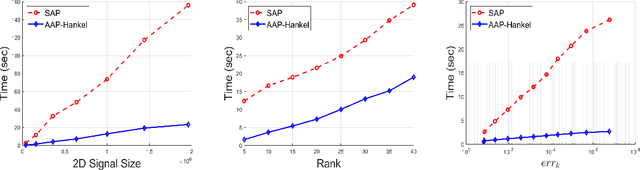
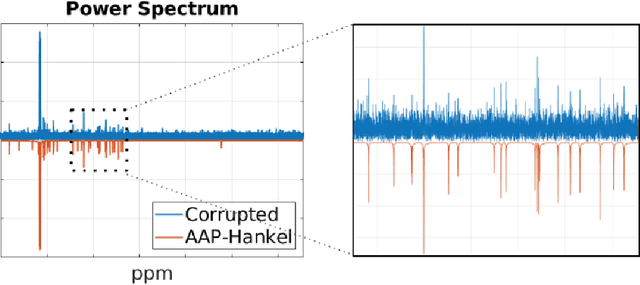
Abstract:Consider a spectrally sparse signal $\boldsymbol{x}$ that consists of $r$ complex sinusoids with or without damping. We study the robust recovery problem for the spectrally sparse signal under the fully observed setting, which is about recovering $\boldsymbol{x}$ and a sparse corruption vector $\boldsymbol{s}$ from their sum $\boldsymbol{z}=\boldsymbol{x}+\boldsymbol{s}$. In this paper, we exploit the low-rank property of the Hankel matrix constructed from $\boldsymbol{x}$, and develop an efficient non-convex algorithm, coined Accelerated Alternating Projections for Robust Low-Rank Hankel Matrix Reconstruction (AAP-Hankel). The high computational efficiency and low space complexity of AAP-Hankel are achieved by fast computations involving structured matrices, and a subspace projection method for accelerated low-rank approximation. Theoretical recovery guarantee with a linear convergence rate has been established for AAP-Hankel. Empirical performance comparisons on synthetic and real-world datasets demonstrate the computational advantages of AAP-Hankel, in both efficiency and robustness aspects.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge