SGD with Dependent Data: Optimal Estimation, Regret, and Inference

This work investigates the performance of the final iterate produced by stochastic gradient descent (SGD) under temporally dependent data. We consider two complementary sources of dependence: $(i)$ martingale-type dependence in both the covariate and noise processes, which accommodates non-stationary and non-mixing time series data, and $(ii)$ dependence induced by sequential decision making. Our formulation runs in parallel with classical notions of (local) stationarity and strong mixing, while neither framework fully subsumes the other. Remarkably, SGD is shown to automatically accommodate both independent and dependent information under a broad class of stepsize schedules and exploration rate schemes. Non-asymptotically, we show that SGD simultaneously achieves statistically optimal estimation error and regret, extending and improving existing results. In particular, our tail bounds remain sharp even for potentially infinite horizon $T=+\infty$. Asymptotically, the SGD iterates converge to a Gaussian distribution with only an $O_{\PP}(1/\sqrt{t})$ remainder, demonstrating that the supposed estimation-regret trade-off claimed in prior work can in fact be avoided. We further propose a new ``conic'' approximation of the decision region that allows the covariates to have unbounded support. For online sparse regression, we develop a new SGD-based algorithm that uses only $d$ units of storage and requires $O(d)$ flops per iteration, achieving the long term statistical optimality. Intuitively, each incoming observation contributes to estimation accuracy, while aggregated summary statistics guide support recovery.

Computationally Efficient and Statistically Optimal Robust High-Dimensional Linear Regression

High-dimensional linear regression under heavy-tailed noise or outlier corruption is challenging, both computationally and statistically. Convex approaches have been proven statistically optimal but suffer from high computational costs, especially since the robust loss functions are usually non-smooth. More recently, computationally fast non-convex approaches via sub-gradient descent are proposed, which, unfortunately, fail to deliver a statistically consistent estimator even under sub-Gaussian noise. In this paper, we introduce a projected sub-gradient descent algorithm for both the sparse linear regression and low-rank linear regression problems. The algorithm is not only computationally efficient with linear convergence but also statistically optimal, be the noise Gaussian or heavy-tailed with a finite 1 + epsilon moment. The convergence theory is established for a general framework and its specific applications to absolute loss, Huber loss and quantile loss are investigated. Compared with existing non-convex methods, ours reveals a surprising phenomenon of two-phase convergence. In phase one, the algorithm behaves as in typical non-smooth optimization that requires gradually decaying stepsizes. However, phase one only delivers a statistically sub-optimal estimator, which is already observed in the existing literature. Interestingly, during phase two, the algorithm converges linearly as if minimizing a smooth and strongly convex objective function, and thus a constant stepsize suffices. Underlying the phase-two convergence is the smoothing effect of random noise to the non-smooth robust losses in an area close but not too close to the truth. Numerical simulations confirm our theoretical discovery and showcase the superiority of our algorithm over prior methods.

Computationally Efficient and Statistically Optimal Robust Low-rank Matrix Estimation

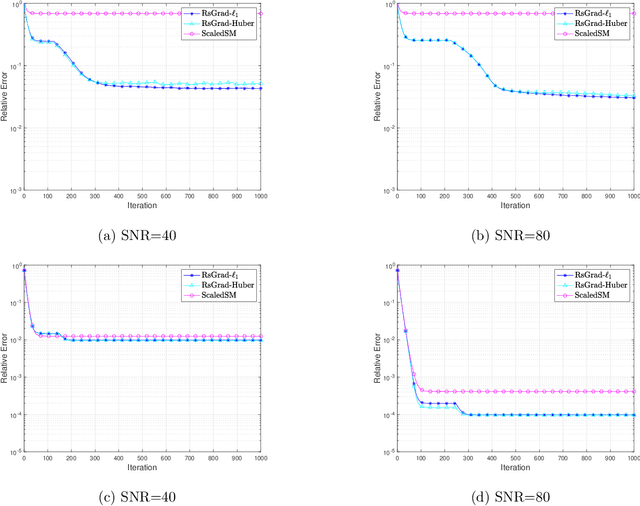
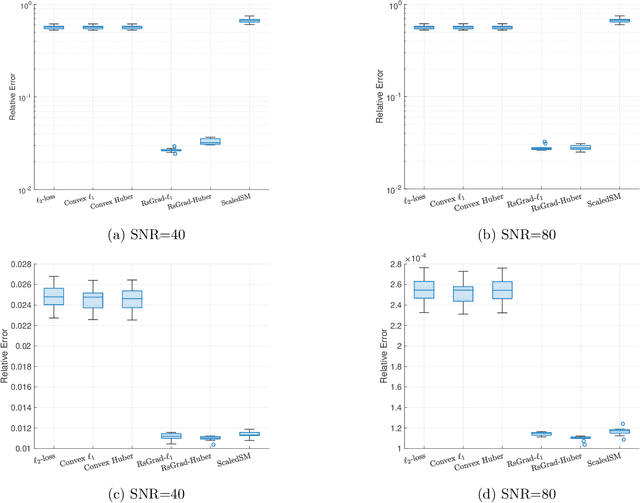
Low-rank matrix estimation under heavy-tailed noise is challenging, both computationally and statistically. Convex approaches have been proven statistically optimal but suffer from high computational costs, especially since robust loss functions are usually non-smooth. More recently, computationally fast non-convex approaches via sub-gradient descent are proposed, which, unfortunately, fail to deliver a statistically consistent estimator even under sub-Gaussian noise. In this paper, we introduce a novel Riemannian sub-gradient (RsGrad) algorithm which is not only computationally efficient with linear convergence but also is statistically optimal, be the noise Gaussian or heavy-tailed. Convergence theory is established for a general framework and specific applications to absolute loss, Huber loss and quantile loss are investigated. Compared with existing non-convex methods, ours reveals a surprising phenomenon of dual-phase convergence. In phase one, RsGrad behaves as in a typical non-smooth optimization that requires gradually decaying stepsizes. However, phase one only delivers a statistically sub-optimal estimator which is already observed in existing literature. Interestingly, during phase two, RsGrad converges linearly as if minimizing a smooth and strongly convex objective function and thus a constant stepsize suffices. Underlying the phase-two convergence is the smoothing effect of random noise to the non-smooth robust losses in an area close but not too close to the truth. Numerical simulations confirm our theoretical discovery and showcase the superiority of RsGrad over prior methods.