Online Network Inference from Graph-Stationary Signals with Hidden Nodes

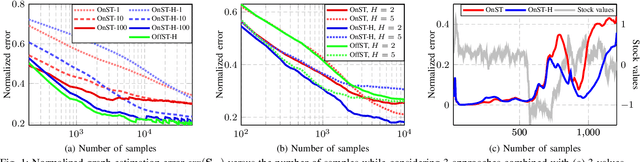
Graph learning is the fundamental task of estimating unknown graph connectivity from available data. Typical approaches assume that not only is all information available simultaneously but also that all nodes can be observed. However, in many real-world scenarios, data can neither be known completely nor obtained all at once. We present a novel method for online graph estimation that accounts for the presence of hidden nodes. We consider signals that are stationary on the underlying graph, which provides a model for the unknown connections to hidden nodes. We then formulate a convex optimization problem for graph learning from streaming, incomplete graph signals. We solve the proposed problem through an efficient proximal gradient algorithm that can run in real-time as data arrives sequentially. Additionally, we provide theoretical conditions under which our online algorithm is similar to batch-wise solutions. Through experimental results on synthetic and real-world data, we demonstrate the viability of our approach for online graph learning in the presence of missing observations.

Fair GLASSO: Estimating Fair Graphical Models with Unbiased Statistical Behavior

We propose estimating Gaussian graphical models (GGMs) that are fair with respect to sensitive nodal attributes. Many real-world models exhibit unfair discriminatory behavior due to biases in data. Such discrimination is known to be exacerbated when data is equipped with pairwise relationships encoded in a graph. Additionally, the effect of biased data on graphical models is largely underexplored. We thus introduce fairness for graphical models in the form of two bias metrics to promote balance in statistical similarities across nodal groups with different sensitive attributes. Leveraging these metrics, we present Fair GLASSO, a regularized graphical lasso approach to obtain sparse Gaussian precision matrices with unbiased statistical dependencies across groups. We also propose an efficient proximal gradient algorithm to obtain the estimates. Theoretically, we express the tradeoff between fair and accurate estimated precision matrices. Critically, this includes demonstrating when accuracy can be preserved in the presence of a fairness regularizer. On top of this, we study the complexity of Fair GLASSO and demonstrate that our algorithm enjoys a fast convergence rate. Our empirical validation includes synthetic and real-world simulations that illustrate the value and effectiveness of our proposed optimization problem and iterative algorithm.

Polynomial Graphical Lasso: Learning Edges from Gaussian Graph-Stationary Signals

This paper introduces Polynomial Graphical Lasso (PGL), a new approach to learning graph structures from nodal signals. Our key contribution lies in modeling the signals as Gaussian and stationary on the graph, enabling the development of a graph-learning formulation that combines the strengths of graphical lasso with a more encompassing model. Specifically, we assume that the precision matrix can take any polynomial form of the sought graph, allowing for increased flexibility in modeling nodal relationships. Given the resulting complexity and nonconvexity of the resulting optimization problem, we (i) propose a low-complexity algorithm that alternates between estimating the graph and precision matrices, and (ii) characterize its convergence. We evaluate the performance of PGL through comprehensive numerical simulations using both synthetic and real data, demonstrating its superiority over several alternatives. Overall, this approach presents a significant advancement in graph learning and holds promise for various applications in graph-aware signal analysis and beyond.

Mitigating Subpopulation Bias for Fair Network Topology Inference

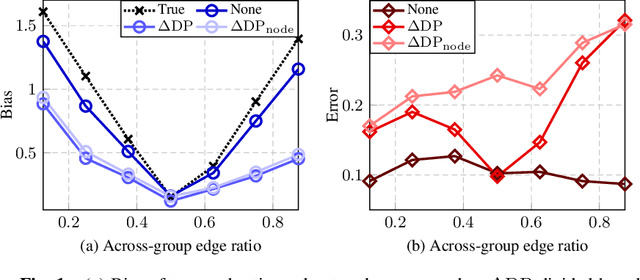
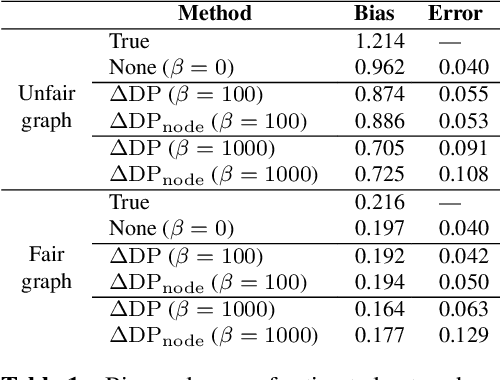
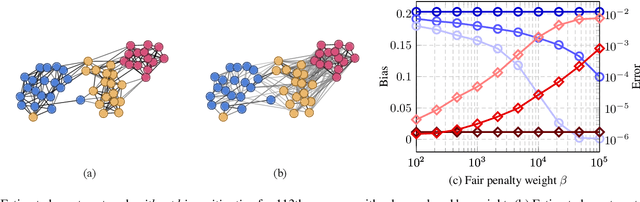
We consider fair network topology inference from nodal observations. Real-world networks often exhibit biased connections based on sensitive nodal attributes. Hence, different subpopulations of nodes may not share or receive information equitably. We thus propose an optimization-based approach to accurately infer networks while discouraging biased edges. To this end, we present bias metrics that measure topological demographic parity to be applied as convex penalties, suitable for most optimization-based graph learning methods. Moreover, we encourage equitable treatment for any number of subpopulations of differing sizes. We validate our method on synthetic and real-world simulations using networks with both biased and unbiased connections.

Learning graphs and simplicial complexes from data

Graphs are widely used to represent complex information and signal domains with irregular support. Typically, the underlying graph topology is unknown and must be estimated from the available data. Common approaches assume pairwise node interactions and infer the graph topology based on this premise. In contrast, our novel method not only unveils the graph topology but also identifies three-node interactions, referred to in the literature as second-order simplicial complexes (SCs). We model signals using a graph autoregressive Volterra framework, enhancing it with structured graph Volterra kernels to learn SCs. We propose a mathematical formulation for graph and SC inference, solving it through convex optimization involving group norms and mask matrices. Experimental results on synthetic and real-world data showcase a superior performance for our approach compared to existing methods.

Joint Network Topology Inference in the Presence of Hidden Nodes

We investigate the increasingly prominent task of jointly inferring multiple networks from nodal observations. While most joint inference methods assume that observations are available at all nodes, we consider the realistic and more difficult scenario where a subset of nodes are hidden and cannot be measured. Under the assumptions that the partially observed nodal signals are graph stationary and the networks have similar connectivity patterns, we derive structural characteristics of the connectivity between hidden and observed nodes. This allows us to formulate an optimization problem for estimating networks while accounting for the influence of hidden nodes. We identify conditions under which a convex relaxation yields the sparsest solution, and we formalize the performance of our proposed optimization problem with respect to the effect of the hidden nodes. Finally, synthetic and real-world simulations provide evaluations of our method in comparison with other baselines.

Graph Learning from Gaussian and Stationary Graph Signals

Graphs have become pervasive tools to represent information and datasets with irregular support. However, in many cases, the underlying graph is either unavailable or naively obtained, calling for more advanced methods to its estimation. Indeed, graph topology inference methods that estimate the network structure from a set of signal observations have a long and well established history. By assuming that the observations are both Gaussian and stationary in the sought graph, this paper proposes a new scheme to learn the network from nodal observations. Consideration of graph stationarity overcomes some of the limitations of the classical Graphical Lasso algorithm, which is constrained to a more specific class of graphical models. On the other hand, Gaussianity allows us to regularize the estimation, requiring less samples than in existing graph stationarity-based approaches. While the resultant estimation (optimization) problem is more complex and non-convex, we design an alternating convex approach able to find a stationary solution. Numerical tests with synthetic and real data are presented, and the performance of our approach is compared with existing alternatives.

Joint graph learning from Gaussian observations in the presence of hidden nodes

Graph learning problems are typically approached by focusing on learning the topology of a single graph when signals from all nodes are available. However, many contemporary setups involve multiple related networks and, moreover, it is often the case that only a subset of nodes is observed while the rest remain hidden. Motivated by this, we propose a joint graph learning method that takes into account the presence of hidden (latent) variables. Intuitively, the presence of the hidden nodes renders the inference task ill-posed and challenging to solve, so we overcome this detrimental influence by harnessing the similarity of the estimated graphs. To that end, we assume that the observed signals are drawn from a Gaussian Markov random field with latent variables and we carefully model the graph similarity among hidden (latent) nodes. Then, we exploit the structure resulting from the previous considerations to propose a convex optimization problem that solves the joint graph learning task by providing a regularized maximum likelihood estimator. Finally, we compare the proposed algorithm with different baselines and evaluate its performance over synthetic and real-world graphs.

Learning Graphs from Smooth and Graph-Stationary Signals with Hidden Variables

Network-topology inference from (vertex) signal observations is a prominent problem across data-science and engineering disciplines. Most existing schemes assume that observations from all nodes are available, but in many practical environments, only a subset of nodes is accessible. A natural (and sometimes effective) approach is to disregard the role of unobserved nodes, but this ignores latent network effects, deteriorating the quality of the estimated graph. Differently, this paper investigates the problem of inferring the topology of a network from nodal observations while taking into account the presence of hidden (latent) variables. Our schemes assume the number of observed nodes is considerably larger than the number of hidden variables and build on recent graph signal processing models to relate the signals and the underlying graph. Specifically, we go beyond classical correlation and partial correlation approaches and assume that the signals are smooth and/or stationary in the sought graph. The assumptions are codified into different constrained optimization problems, with the presence of hidden variables being explicitly taken into account. Since the resulting problems are ill-conditioned and non-convex, the block matrix structure of the proposed formulations is leveraged and suitable convex-regularized relaxations are presented. Numerical experiments over synthetic and real-world datasets showcase the performance of the developed methods and compare them with existing alternatives.

Joint inference of multiple graphs with hidden variables from stationary graph signals

Learning graphs from sets of nodal observations represents a prominent problem formally known as graph topology inference. However, current approaches are limited by typically focusing on inferring single networks, and they assume that observations from all nodes are available. First, many contemporary setups involve multiple related networks, and second, it is often the case that only a subset of nodes is observed while the rest remain hidden. Motivated by these facts, we introduce a joint graph topology inference method that models the influence of the hidden variables. Under the assumptions that the observed signals are stationary on the sought graphs and the graphs are closely related, the joint estimation of multiple networks allows us to exploit such relationships to improve the quality of the learned graphs. Moreover, we confront the challenging problem of modeling the influence of the hidden nodes to minimize their detrimental effect. To obtain an amenable approach, we take advantage of the particular structure of the setup at hand and leverage the similarity between the different graphs, which affects both the observed and the hidden nodes. To test the proposed method, numerical simulations over synthetic and real-world graphs are provided.