Adapting to Heterophilic Graph Data with Structure-Guided Neighbor Discovery

Graph Neural Networks (GNNs) often struggle with heterophilic data, where connected nodes may have dissimilar labels, as they typically assume homophily and rely on local message passing. To address this, we propose creating alternative graph structures by linking nodes with similar structural attributes (e.g., role-based or global), thereby fostering higher label homophily on these new graphs. We theoretically prove that GNN performance can be improved by utilizing graphs with fewer false positive edges (connections between nodes of different classes) and that considering multiple graph views increases the likelihood of finding such beneficial structures. Building on these insights, we introduce Structure-Guided GNN (SG-GNN), an architecture that processes the original graph alongside the newly created structural graphs, adaptively learning to weigh their contributions. Extensive experiments on various benchmark datasets, particularly those with heterophilic characteristics, demonstrate that our SG-GNN achieves state-of-the-art or highly competitive performance, highlighting the efficacy of exploiting structural information to guide GNNs.

Structure-Guided Input Graph for GNNs facing Heterophily

Graph Neural Networks (GNNs) have emerged as a promising tool to handle data exhibiting an irregular structure. However, most GNN architectures perform well on homophilic datasets, where the labels of neighboring nodes are likely to be the same. In recent years, an increasing body of work has been devoted to the development of GNN architectures for heterophilic datasets, where labels do not exhibit this low-pass behavior. In this work, we create a new graph in which nodes are connected if they share structural characteristics, meaning a higher chance of sharing their labels, and then use this new graph in the GNN architecture. To do this, we compute the k-nearest neighbors graph according to distances between structural features, which are either (i) role-based, such as degree, or (ii) global, such as centrality measures. Experiments show that the labels are smoother in this newly defined graph and that the performance of GNN architectures improves when using this alternative structure.

ML-SPEAK: A Theory-Guided Machine Learning Method for Studying and Predicting Conversational Turn-taking Patterns

Predicting team dynamics from personality traits remains a fundamental challenge for the psychological sciences and team-based organizations. Understanding how team composition generates team processes can significantly advance team-based research along with providing practical guidelines for team staffing and training. Although the Input-Process-Output (IPO) model has been useful for studying these connections, the complex nature of team member interactions demands a more dynamic approach. We develop a computational model of conversational turn-taking within self-organized teams that can provide insight into the relationships between team member personality traits and team communication dynamics. We focus on turn-taking patterns between team members, independent of content, which can significantly influence team emergent states and outcomes while being objectively measurable and quantifiable. As our model is trained on conversational data from teams of given trait compositions, it can learn the relationships between individual traits and speaking behaviors and predict group-wide patterns of communication based on team trait composition alone. We first evaluate the performance of our model using simulated data and then apply it to real-world data collected from self-organized student teams. In comparison to baselines, our model is more accurate at predicting speaking turn sequences and can reveal new relationships between team member traits and their communication patterns. Our approach offers a more data-driven and dynamic understanding of team processes. By bridging the gap between individual personality traits and team communication patterns, our model has the potential to inform theories of team processes and provide powerful insights into optimizing team staffing and training.

Low-Rank Tensors for Multi-Dimensional Markov Models

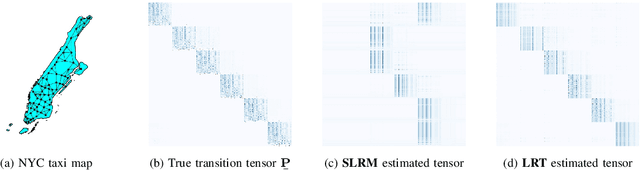
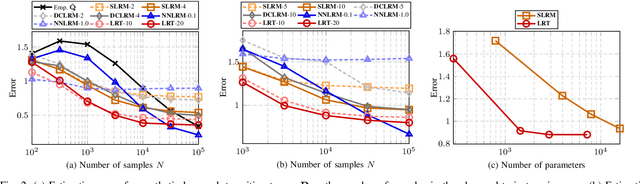
This work presents a low-rank tensor model for multi-dimensional Markov chains. A common approach to simplify the dynamical behavior of a Markov chain is to impose low-rankness on the transition probability matrix. Inspired by the success of these matrix techniques, we present low-rank tensors for representing transition probabilities on multi-dimensional state spaces. Through tensor decomposition, we provide a connection between our method and classical probabilistic models. Moreover, our proposed model yields a parsimonious representation with fewer parameters than matrix-based approaches. Unlike these methods, which impose low-rankness uniformly across all states, our tensor method accounts for the multi-dimensionality of the state space. We also propose an optimization-based approach to estimate a Markov model as a low-rank tensor. Our optimization problem can be solved by the alternating direction method of multipliers (ADMM), which enjoys convergence to a stationary solution. We empirically demonstrate that our tensor model estimates Markov chains more efficiently than conventional techniques, requiring both fewer samples and parameters. We perform numerical simulations for both a synthetic low-rank Markov chain and a real-world example with New York City taxi data, showcasing the advantages of multi-dimensionality for modeling state spaces.

Online Network Inference from Graph-Stationary Signals with Hidden Nodes

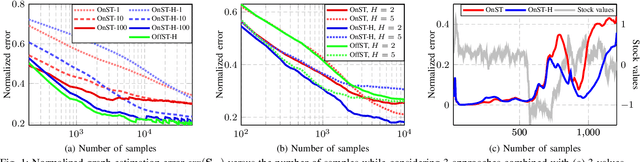
Graph learning is the fundamental task of estimating unknown graph connectivity from available data. Typical approaches assume that not only is all information available simultaneously but also that all nodes can be observed. However, in many real-world scenarios, data can neither be known completely nor obtained all at once. We present a novel method for online graph estimation that accounts for the presence of hidden nodes. We consider signals that are stationary on the underlying graph, which provides a model for the unknown connections to hidden nodes. We then formulate a convex optimization problem for graph learning from streaming, incomplete graph signals. We solve the proposed problem through an efficient proximal gradient algorithm that can run in real-time as data arrives sequentially. Additionally, we provide theoretical conditions under which our online algorithm is similar to batch-wise solutions. Through experimental results on synthetic and real-world data, we demonstrate the viability of our approach for online graph learning in the presence of missing observations.

Redesigning graph filter-based GNNs to relax the homophily assumption

Graph neural networks (GNNs) have become a workhorse approach for learning from data defined over irregular domains, typically by implicitly assuming that the data structure is represented by a homophilic graph. However, recent works have revealed that many relevant applications involve heterophilic data where the performance of GNNs can be notably compromised. To address this challenge, we present a simple yet effective architecture designed to mitigate the limitations of the homophily assumption. The proposed architecture reinterprets the role of graph filters in convolutional GNNs, resulting in a more general architecture while incorporating a stronger inductive bias than GNNs based on filter banks. The proposed convolutional layer enhances the expressive capacity of the architecture enabling it to learn from both homophilic and heterophilic data and preventing the issue of oversmoothing. From a theoretical standpoint, we show that the proposed architecture is permutation equivariant. Finally, we show that the proposed GNNs compares favorably relative to several state-of-the-art baselines in both homophilic and heterophilic datasets, showcasing its promising potential.

Fair CoVariance Neural Networks

Covariance-based data processing is widespread across signal processing and machine learning applications due to its ability to model data interconnectivities and dependencies. However, harmful biases in the data may become encoded in the sample covariance matrix and cause data-driven methods to treat different subpopulations unfairly. Existing works such as fair principal component analysis (PCA) mitigate these effects, but remain unstable in low sample regimes, which in turn may jeopardize the fairness goal. To address both biases and instability, we propose Fair coVariance Neural Networks (FVNNs), which perform graph convolutions on the covariance matrix for both fair and accurate predictions. Our FVNNs provide a flexible model compatible with several existing bias mitigation techniques. In particular, FVNNs allow for mitigating the bias in two ways: first, they operate on fair covariance estimates that remove biases from their principal components; second, they are trained in an end-to-end fashion via a fairness regularizer in the loss function so that the model parameters are tailored to solve the task directly in a fair manner. We prove that FVNNs are intrinsically fairer than analogous PCA approaches thanks to their stability in low sample regimes. We validate the robustness and fairness of our model on synthetic and real-world data, showcasing the flexibility of FVNNs along with the tradeoff between fair and accurate performance.

Fair GLASSO: Estimating Fair Graphical Models with Unbiased Statistical Behavior

We propose estimating Gaussian graphical models (GGMs) that are fair with respect to sensitive nodal attributes. Many real-world models exhibit unfair discriminatory behavior due to biases in data. Such discrimination is known to be exacerbated when data is equipped with pairwise relationships encoded in a graph. Additionally, the effect of biased data on graphical models is largely underexplored. We thus introduce fairness for graphical models in the form of two bias metrics to promote balance in statistical similarities across nodal groups with different sensitive attributes. Leveraging these metrics, we present Fair GLASSO, a regularized graphical lasso approach to obtain sparse Gaussian precision matrices with unbiased statistical dependencies across groups. We also propose an efficient proximal gradient algorithm to obtain the estimates. Theoretically, we express the tradeoff between fair and accurate estimated precision matrices. Critically, this includes demonstrating when accuracy can be preserved in the presence of a fairness regularizer. On top of this, we study the complexity of Fair GLASSO and demonstrate that our algorithm enjoys a fast convergence rate. Our empirical validation includes synthetic and real-world simulations that illustrate the value and effectiveness of our proposed optimization problem and iterative algorithm.

Mitigating Subpopulation Bias for Fair Network Topology Inference

We consider fair network topology inference from nodal observations. Real-world networks often exhibit biased connections based on sensitive nodal attributes. Hence, different subpopulations of nodes may not share or receive information equitably. We thus propose an optimization-based approach to accurately infer networks while discouraging biased edges. To this end, we present bias metrics that measure topological demographic parity to be applied as convex penalties, suitable for most optimization-based graph learning methods. Moreover, we encourage equitable treatment for any number of subpopulations of differing sizes. We validate our method on synthetic and real-world simulations using networks with both biased and unbiased connections.

Recovering Missing Node Features with Local Structure-based Embeddings

Node features bolster graph-based learning when exploited jointly with network structure. However, a lack of nodal attributes is prevalent in graph data. We present a framework to recover completely missing node features for a set of graphs, where we only know the signals of a subset of graphs. Our approach incorporates prior information from both graph topology and existing nodal values. We demonstrate an example implementation of our framework where we assume that node features depend on local graph structure. Missing nodal values are estimated by aggregating known features from the most similar nodes. Similarity is measured through a node embedding space that preserves local topological features, which we train using a Graph AutoEncoder. We empirically show not only the accuracy of our feature estimation approach but also its value for downstream graph classification. Our success embarks on and implies the need to emphasize the relationship between node features and graph structure in graph-based learning.