Sergio Rozada
Graph-Aware Diffusion for Signal Generation
Oct 06, 2025Abstract:We study the problem of generating graph signals from unknown distributions defined over given graphs, relevant to domains such as recommender systems or sensor networks. Our approach builds on generative diffusion models, which are well established in vision and graph generation but remain underexplored for graph signals. Existing methods lack generality, either ignoring the graph structure in the forward process or designing graph-aware mechanisms tailored to specific domains. We adopt a forward process that incorporates the graph through the heat equation. Rather than relying on the standard formulation, we consider a time-warped coefficient to mitigate the exponential decay of the drift term, yielding a graph-aware generative diffusion model (GAD). We analyze its forward dynamics, proving convergence to a Gaussian Markov random field with covariance parametrized by the graph Laplacian, and interpret the backward dynamics as a sequence of graph-signal denoising problems. Finally, we demonstrate the advantages of GAD on synthetic data, real traffic speed measurements, and a temperature sensor network.
A Tensor Low-Rank Approximation for Value Functions in Multi-Task Reinforcement Learning
Jan 17, 2025

Abstract:In pursuit of reinforcement learning systems that could train in physical environments, we investigate multi-task approaches as a means to alleviate the need for massive data acquisition. In a tabular scenario where the Q-functions are collected across tasks, we model our learning problem as optimizing a higher order tensor structure. Recognizing that close-related tasks may require similar actions, our proposed method imposes a low-rank condition on this aggregated Q-tensor. The rationale behind this approach to multi-task learning is that the low-rank structure enforces the notion of similarity, without the need to explicitly prescribe which tasks are similar, but inferring this information from a reduced amount of data simultaneously with the stochastic optimization of the Q-tensor. The efficiency of our low-rank tensor approach to multi-task learning is demonstrated in two numerical experiments, first in a benchmark environment formed by a collection of inverted pendulums, and then into a practical scenario involving multiple wireless communication devices.
Solving Finite-Horizon MDPs via Low-Rank Tensors
Jan 17, 2025



Abstract:We study the problem of learning optimal policies in finite-horizon Markov Decision Processes (MDPs) using low-rank reinforcement learning (RL) methods. In finite-horizon MDPs, the policies, and therefore the value functions (VFs) are not stationary. This aggravates the challenges of high-dimensional MDPs, as they suffer from the curse of dimensionality and high sample complexity. To address these issues, we propose modeling the VFs of finite-horizon MDPs as low-rank tensors, enabling a scalable representation that renders the problem of learning optimal policies tractable. We introduce an optimization-based framework for solving the Bellman equations with low-rank constraints, along with block-coordinate descent (BCD) and block-coordinate gradient descent (BCGD) algorithms, both with theoretical convergence guarantees. For scenarios where the system dynamics are unknown, we adapt the proposed BCGD method to estimate the VFs using sampled trajectories. Numerical experiments further demonstrate that the proposed framework reduces computational demands in controlled synthetic scenarios and more realistic resource allocation problems.
Multilinear Tensor Low-Rank Approximation for Policy-Gradient Methods in Reinforcement Learning
Jan 08, 2025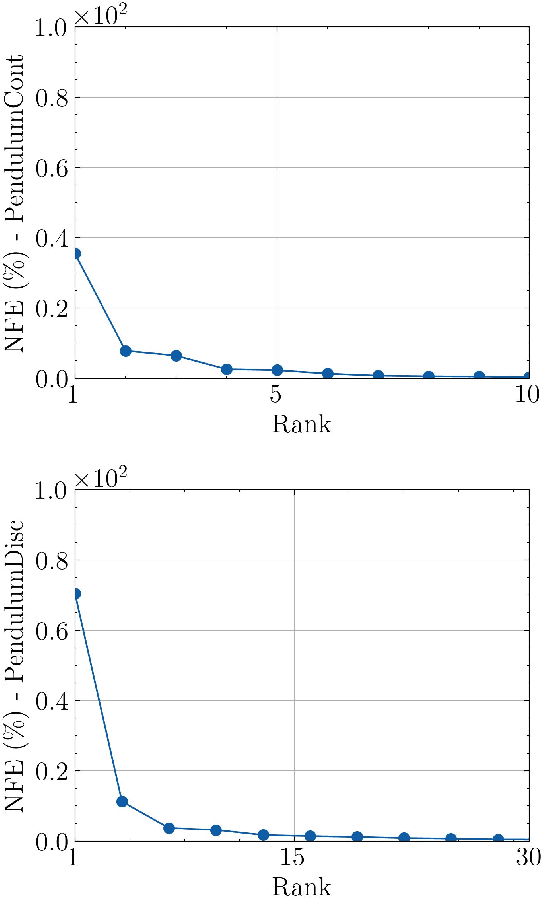
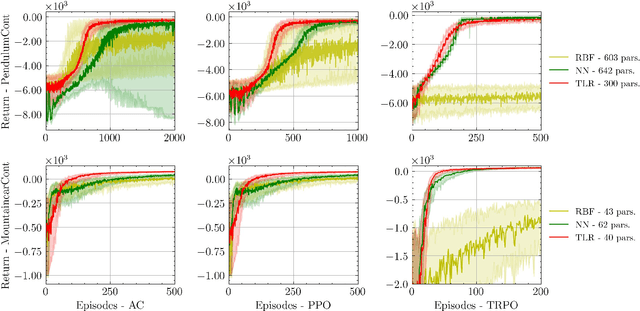
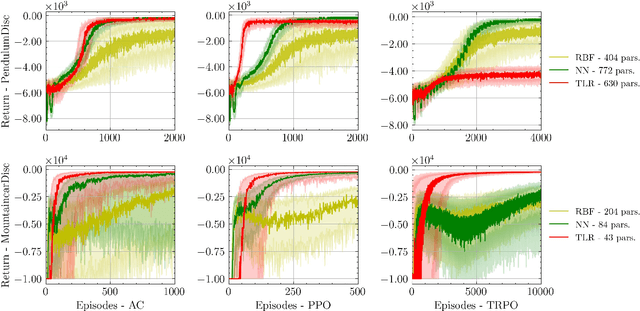
Abstract:Reinforcement learning (RL) aims to estimate the action to take given a (time-varying) state, with the goal of maximizing a cumulative reward function. Predominantly, there are two families of algorithms to solve RL problems: value-based and policy-based methods, with the latter designed to learn a probabilistic parametric policy from states to actions. Most contemporary approaches implement this policy using a neural network (NN). However, NNs usually face issues related to convergence, architectural suitability, hyper-parameter selection, and underutilization of the redundancies of the state-action representations (e.g. locally similar states). This paper postulates multi-linear mappings to efficiently estimate the parameters of the RL policy. More precisely, we leverage the PARAFAC decomposition to design tensor low-rank policies. The key idea involves collecting the policy parameters into a tensor and leveraging tensor-completion techniques to enforce low rank. We establish theoretical guarantees of the proposed methods for various policy classes and validate their efficacy through numerical experiments. Specifically, we demonstrate that tensor low-rank policy models reduce computational and sample complexities in comparison to NN models while achieving similar rewards.
Low-Rank Tensors for Multi-Dimensional Markov Models
Nov 04, 2024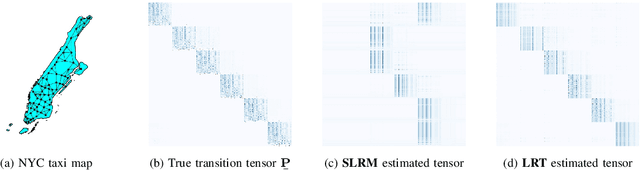
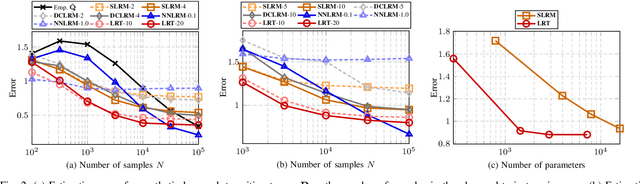
Abstract:This work presents a low-rank tensor model for multi-dimensional Markov chains. A common approach to simplify the dynamical behavior of a Markov chain is to impose low-rankness on the transition probability matrix. Inspired by the success of these matrix techniques, we present low-rank tensors for representing transition probabilities on multi-dimensional state spaces. Through tensor decomposition, we provide a connection between our method and classical probabilistic models. Moreover, our proposed model yields a parsimonious representation with fewer parameters than matrix-based approaches. Unlike these methods, which impose low-rankness uniformly across all states, our tensor method accounts for the multi-dimensionality of the state space. We also propose an optimization-based approach to estimate a Markov model as a low-rank tensor. Our optimization problem can be solved by the alternating direction method of multipliers (ADMM), which enjoys convergence to a stationary solution. We empirically demonstrate that our tensor model estimates Markov chains more efficiently than conventional techniques, requiring both fewer samples and parameters. We perform numerical simulations for both a synthetic low-rank Markov chain and a real-world example with New York City taxi data, showcasing the advantages of multi-dimensionality for modeling state spaces.
Deterministic Policy Gradient Primal-Dual Methods for Continuous-Space Constrained MDPs
Aug 19, 2024



Abstract:We study the problem of computing deterministic optimal policies for constrained Markov decision processes (MDPs) with continuous state and action spaces, which are widely encountered in constrained dynamical systems. Designing deterministic policy gradient methods in continuous state and action spaces is particularly challenging due to the lack of enumerable state-action pairs and the adoption of deterministic policies, hindering the application of existing policy gradient methods for constrained MDPs. To this end, we develop a deterministic policy gradient primal-dual method to find an optimal deterministic policy with non-asymptotic convergence. Specifically, we leverage regularization of the Lagrangian of the constrained MDP to propose a deterministic policy gradient primal-dual (D-PGPD) algorithm that updates the deterministic policy via a quadratic-regularized gradient ascent step and the dual variable via a quadratic-regularized gradient descent step. We prove that the primal-dual iterates of D-PGPD converge at a sub-linear rate to an optimal regularized primal-dual pair. We instantiate D-PGPD with function approximation and prove that the primal-dual iterates of D-PGPD converge at a sub-linear rate to an optimal regularized primal-dual pair, up to a function approximation error. Furthermore, we demonstrate the effectiveness of our method in two continuous control problems: robot navigation and fluid control. To the best of our knowledge, this appears to be the first work that proposes a deterministic policy search method for continuous-space constrained MDPs.
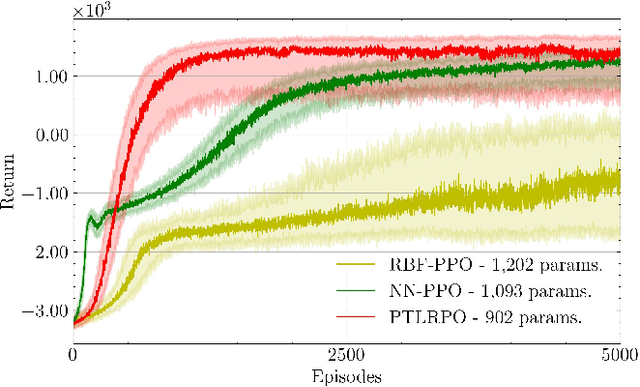
Matrix Low-Rank Trust Region Policy Optimization
May 27, 2024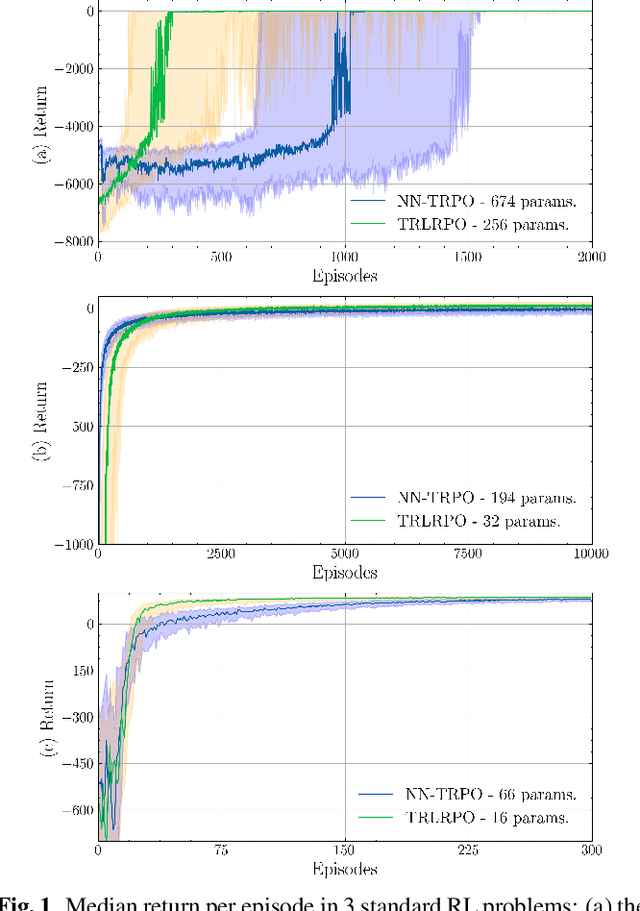
Abstract:Most methods in reinforcement learning use a Policy Gradient (PG) approach to learn a parametric stochastic policy that maps states to actions. The standard approach is to implement such a mapping via a neural network (NN) whose parameters are optimized using stochastic gradient descent. However, PG methods are prone to large policy updates that can render learning inefficient. Trust region algorithms, like Trust Region Policy Optimization (TRPO), constrain the policy update step, ensuring monotonic improvements. This paper introduces low-rank matrix-based models as an efficient alternative for estimating the parameters of TRPO algorithms. By gathering the stochastic policy's parameters into a matrix and applying matrix-completion techniques, we promote and enforce low rank. Our numerical studies demonstrate that low-rank matrix-based policy models effectively reduce both computational and sample complexities compared to NN models, while maintaining comparable aggregated rewards.
Tensor Low-rank Approximation of Finite-horizon Value Functions
May 27, 2024

Abstract:The goal of reinforcement learning is estimating a policy that maps states to actions and maximizes the cumulative reward of a Markov Decision Process (MDP). This is oftentimes achieved by estimating first the optimal (reward) value function (VF) associated with each state-action pair. When the MDP has an infinite horizon, the optimal VFs and policies are stationary under mild conditions. However, in finite-horizon MDPs, the VFs (hence, the policies) vary with time. This poses a challenge since the number of VFs to estimate grows not only with the size of the state-action space but also with the time horizon. This paper proposes a non-parametric low-rank stochastic algorithm to approximate the VFs of finite-horizon MDPs. First, we represent the (unknown) VFs as a multi-dimensional array, or tensor, where time is one of the dimensions. Then, we use rewards sampled from the MDP to estimate the optimal VFs. More precisely, we use the (truncated) PARAFAC decomposition to design an online low-rank algorithm that recovers the entries of the tensor of VFs. The size of the low-rank PARAFAC model grows additively with respect to each of its dimensions, rendering our approach efficient, as demonstrated via numerical experiments.
Matrix Low-Rank Approximation For Policy Gradient Methods
May 27, 2024
Abstract:Estimating a policy that maps states to actions is a central problem in reinforcement learning. Traditionally, policies are inferred from the so called value functions (VFs), but exact VF computation suffers from the curse of dimensionality. Policy gradient (PG) methods bypass this by learning directly a parametric stochastic policy. Typically, the parameters of the policy are estimated using neural networks (NNs) tuned via stochastic gradient descent. However, finding adequate NN architectures can be challenging, and convergence issues are common as well. In this paper, we put forth low-rank matrix-based models to estimate efficiently the parameters of PG algorithms. We collect the parameters of the stochastic policy into a matrix, and then, we leverage matrix-completion techniques to promote (enforce) low rank. We demonstrate via numerical studies how low-rank matrix-based policy models reduce the computational and sample complexities relative to NN models, while achieving a similar aggregated reward.
Tensor and Matrix Low-Rank Value-Function Approximation in Reinforcement Learning
Jan 21, 2022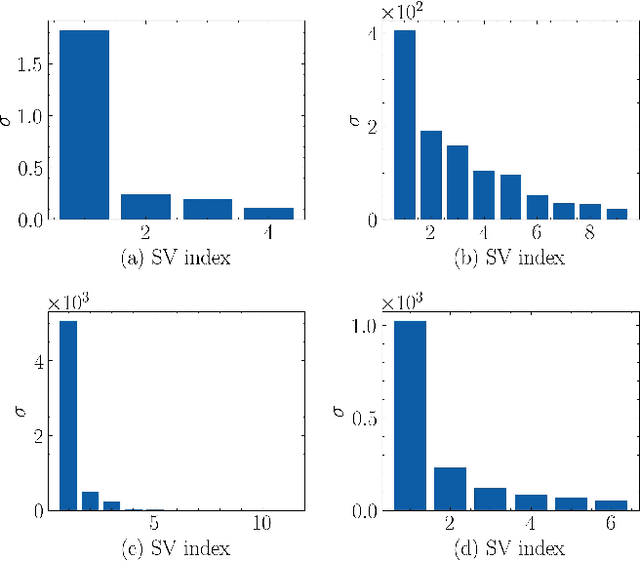
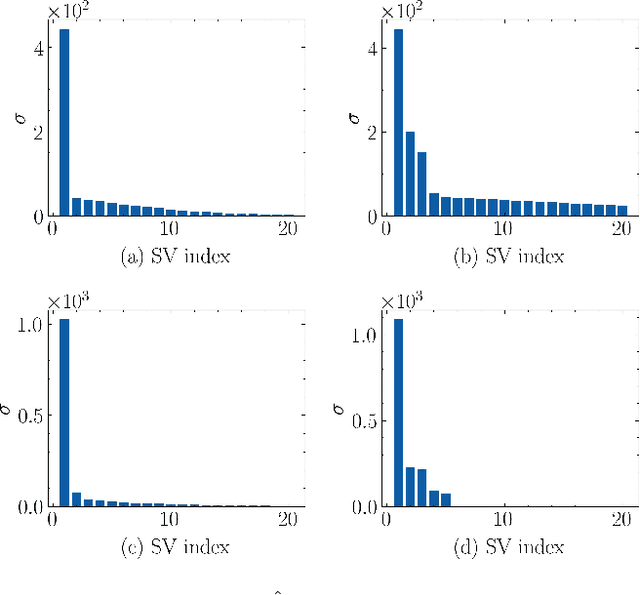
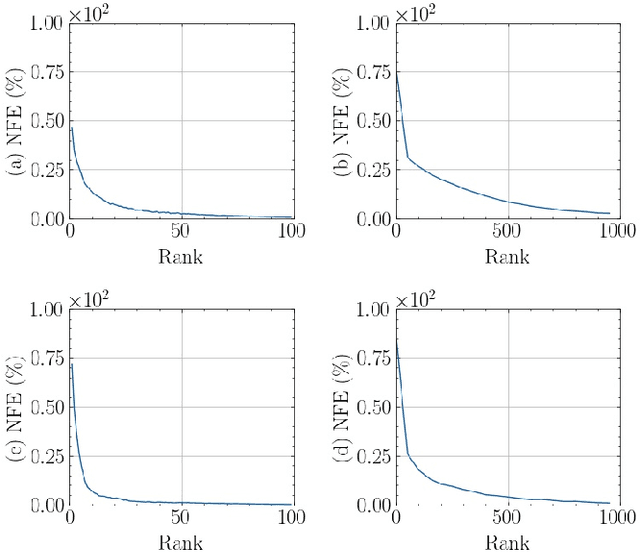
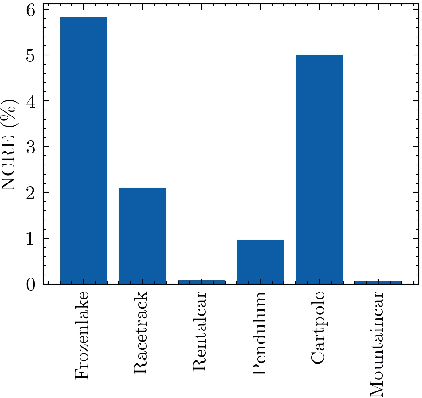
Abstract:Value-function (VF) approximation is a central problem in Reinforcement Learning (RL). Classical non-parametric VF estimation suffers from the curse of dimensionality. As a result, parsimonious parametric models have been adopted to approximate VFs in high-dimensional spaces, with most efforts being focused on linear and neural-network-based approaches. Differently, this paper puts forth a a parsimonious non-parametric approach, where we use stochastic low-rank algorithms to estimate the VF matrix in an online and model-free fashion. Furthermore, as VFs tend to be multi-dimensional, we propose replacing the classical VF matrix representation with a tensor (multi-way array) representation and, then, use the PARAFAC decomposition to design an online model-free tensor low-rank algorithm. Different versions of the algorithms are proposed, their complexity is analyzed, and their performance is assessed numerically using standardized RL environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge