Hoi-To Wai
Katie
Learning Graph from Smooth Signals under Partial Observation: A Robustness Analysis
Sep 18, 2025Abstract:Learning the graph underlying a networked system from nodal signals is crucial to downstream tasks in graph signal processing and machine learning. The presence of hidden nodes whose signals are not observable might corrupt the estimated graph. While existing works proposed various robustifications of vanilla graph learning objectives by explicitly accounting for the presence of these hidden nodes, a robustness analysis of "naive", hidden-node agnostic approaches is still underexplored. This work demonstrates that vanilla graph topology learning methods are implicitly robust to partial observations of low-pass filtered graph signals. We achieve this theoretical result through extending the restricted isometry property (RIP) to the Dirichlet energy function used in graph learning objectives. We show that smoothness-based graph learning formulation (e.g., the GL-SigRep method) on partial observations can recover the ground truth graph topology corresponding to the observed nodes. Synthetic and real data experiments corroborate our findings.
Stochastic Gradient Descent with Strategic Querying
Aug 23, 2025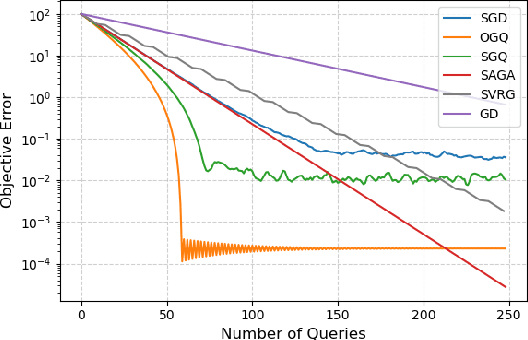
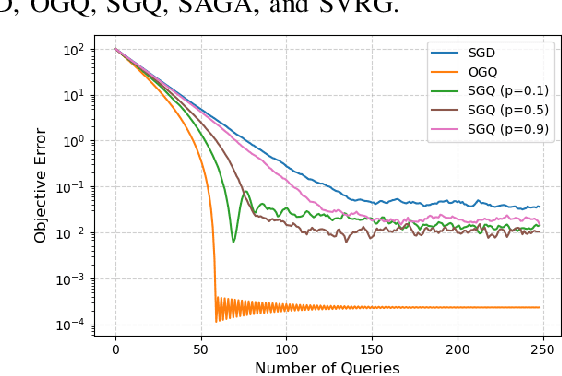
Abstract:This paper considers a finite-sum optimization problem under first-order queries and investigates the benefits of strategic querying on stochastic gradient-based methods compared to uniform querying strategy. We first introduce Oracle Gradient Querying (OGQ), an idealized algorithm that selects one user's gradient yielding the largest possible expected improvement (EI) at each step. However, OGQ assumes oracle access to the gradients of all users to make such a selection, which is impractical in real-world scenarios. To address this limitation, we propose Strategic Gradient Querying (SGQ), a practical algorithm that has better transient-state performance than SGD while making only one query per iteration. For smooth objective functions satisfying the Polyak-Lojasiewicz condition, we show that under the assumption of EI heterogeneity, OGQ enhances transient-state performance and reduces steady-state variance, while SGQ improves transient-state performance over SGD. Our numerical experiments validate our theoretical findings.
Federated Majorize-Minimization: Beyond Parameter Aggregation
Jul 23, 2025Abstract:This paper proposes a unified approach for designing stochastic optimization algorithms that robustly scale to the federated learning setting. Our work studies a class of Majorize-Minimization (MM) problems, which possesses a linearly parameterized family of majorizing surrogate functions. This framework encompasses (proximal) gradient-based algorithms for (regularized) smooth objectives, the Expectation Maximization algorithm, and many problems seen as variational surrogate MM. We show that our framework motivates a unifying algorithm called Stochastic Approximation Stochastic Surrogate MM (\SSMM), which includes previous stochastic MM procedures as special instances. We then extend \SSMM\ to the federated setting, while taking into consideration common bottlenecks such as data heterogeneity, partial participation, and communication constraints; this yields \QSMM. The originality of \QSMM\ is to learn locally and then aggregate information characterizing the \textit{surrogate majorizing function}, contrary to classical algorithms which learn and aggregate the \textit{original parameter}. Finally, to showcase the flexibility of this methodology beyond our theoretical setting, we use it to design an algorithm for computing optimal transport maps in the federated setting.
RoSTE: An Efficient Quantization-Aware Supervised Fine-Tuning Approach for Large Language Models
Feb 13, 2025Abstract:Supervised fine-tuning is a standard method for adapting pre-trained large language models (LLMs) to downstream tasks. Quantization has been recently studied as a post-training technique for efficient LLM deployment. To obtain quantized fine-tuned LLMs, conventional pipelines would first fine-tune the pre-trained models, followed by post-training quantization. This often yields suboptimal performance as it fails to leverage the synergy between fine-tuning and quantization. To effectively realize low-bit quantization of weights, activations, and KV caches in LLMs, we propose an algorithm named Rotated Straight-Through-Estimator (RoSTE), which combines quantization-aware supervised fine-tuning (QA-SFT) with an adaptive rotation strategy that identifies an effective rotation configuration to reduce activation outliers. We provide theoretical insights on RoSTE by analyzing its prediction error when applied to an overparameterized least square quantized training problem. Our findings reveal that the prediction error is directly proportional to the quantization error of the converged weights, which can be effectively managed through an optimized rotation configuration. Experiments on Pythia and Llama models of different sizes demonstrate the effectiveness of RoSTE. Compared to existing post-SFT quantization baselines, our method consistently achieves superior performances across various tasks and different LLM architectures.
Multilinear Tensor Low-Rank Approximation for Policy-Gradient Methods in Reinforcement Learning
Jan 08, 2025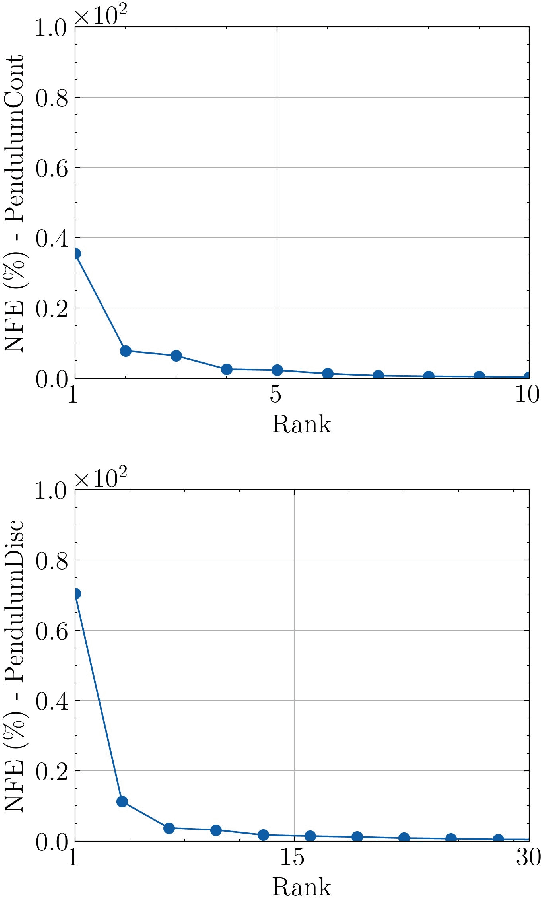
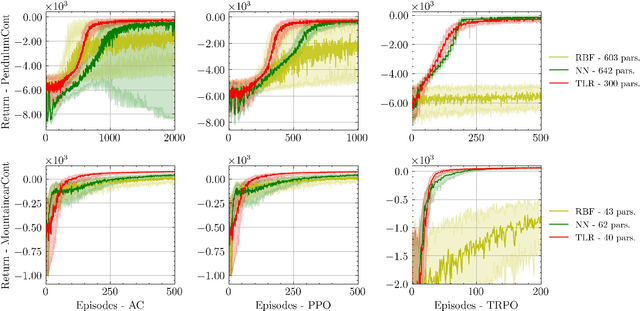
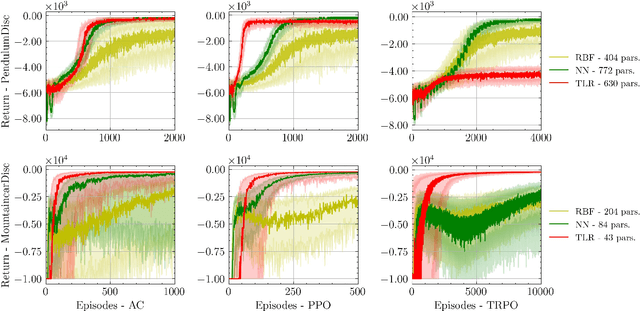
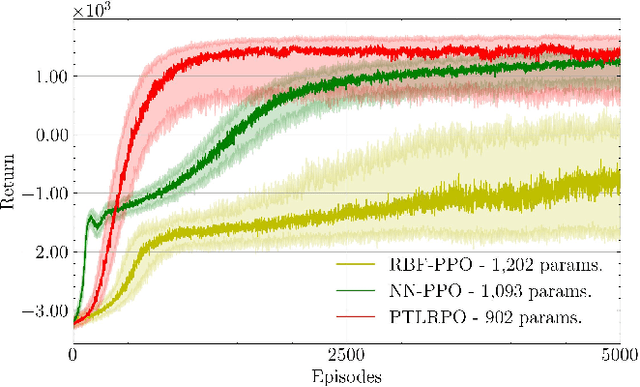
Abstract:Reinforcement learning (RL) aims to estimate the action to take given a (time-varying) state, with the goal of maximizing a cumulative reward function. Predominantly, there are two families of algorithms to solve RL problems: value-based and policy-based methods, with the latter designed to learn a probabilistic parametric policy from states to actions. Most contemporary approaches implement this policy using a neural network (NN). However, NNs usually face issues related to convergence, architectural suitability, hyper-parameter selection, and underutilization of the redundancies of the state-action representations (e.g. locally similar states). This paper postulates multi-linear mappings to efficiently estimate the parameters of the RL policy. More precisely, we leverage the PARAFAC decomposition to design tensor low-rank policies. The key idea involves collecting the policy parameters into a tensor and leveraging tensor-completion techniques to enforce low rank. We establish theoretical guarantees of the proposed methods for various policy classes and validate their efficacy through numerical experiments. Specifically, we demonstrate that tensor low-rank policy models reduce computational and sample complexities in comparison to NN models while achieving similar rewards.
Network Games Induced Prior for Graph Topology Learning
Oct 31, 2024Abstract:Learning the graph topology of a complex network is challenging due to limited data availability and imprecise data models. A common remedy in existing works is to incorporate priors such as sparsity or modularity which highlight on the structural property of graph topology. We depart from these approaches to develop priors that are directly inspired by complex network dynamics. Focusing on social networks with actions modeled by equilibriums of linear quadratic games, we postulate that the social network topologies are optimized with respect to a social welfare function. Utilizing this prior knowledge, we propose a network games induced regularizer to assist graph learning. We then formulate the graph topology learning problem as a bilevel program. We develop a two-timescale gradient algorithm to tackle the latter. We draw theoretical insights on the optimal graph structure of the bilevel program and show that they agree with the topology in several man-made networks. Empirically, we demonstrate the proposed formulation gives rise to reliable estimate of graph topology.
Fully Stochastic Primal-dual Gradient Algorithm for Non-convex Optimization on Random Graphs
Oct 24, 2024



Abstract:Stochastic decentralized optimization algorithms often suffer from issues such as synchronization overhead and intermittent communication. This paper proposes a $\underline{\rm F}$ully $\underline{\rm S}$tochastic $\underline{\rm P}$rimal $\underline{\rm D}$ual gradient $\underline{\rm A}$lgorithm (FSPDA) that suggests an asynchronous decentralized procedure with (i) sparsified non-blocking communication on random undirected graphs and (ii) local stochastic gradient updates. FSPDA allows multiple local gradient steps to accelerate convergence to stationarity while finding a consensual solution with stochastic primal-dual updates. For problems with smooth (possibly non-convex) objective function, we show that FSPDA converges to an $\mathrm{\mathcal{O}( {\it \sigma /\sqrt{nT}} )}$-stationary solution after $\mathrm{\it T}$ iterations without assuming data heterogeneity. The performance of FSPDA is on par with state-of-the-art algorithms whose convergence depend on static graph and synchronous updates. To our best knowledge, FSPDA is the first asynchronous algorithm that converges exactly under the non-convex setting. Numerical experiments are presented to show the benefits of FSPDA.
Getting More Juice Out of the SFT Data: Reward Learning from Human Demonstration Improves SFT for LLM Alignment
May 29, 2024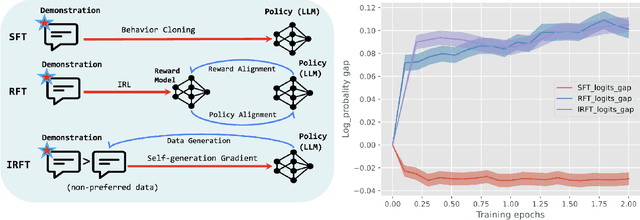

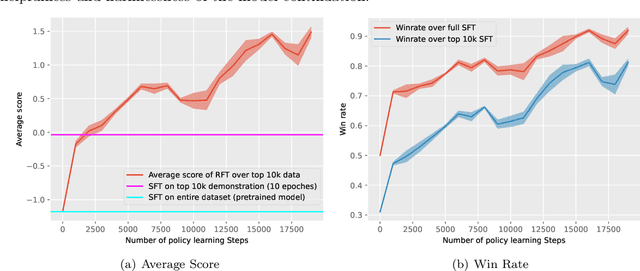
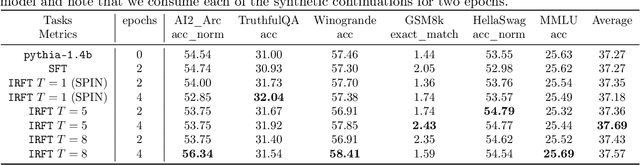
Abstract:Aligning human preference and value is an important requirement for contemporary foundation models. State-of-the-art techniques such as Reinforcement Learning from Human Feedback (RLHF) often consist of two stages: 1) supervised fine-tuning (SFT), where the model is fine-tuned by learning from human demonstration data; 2) Preference learning, where preference data is used to learn a reward model, which is in turn used by a reinforcement learning (RL) step to fine-tune the model. Such reward model serves as a proxy to human preference, and it is critical to guide the RL step towards improving the model quality. In this work, we argue that the SFT stage significantly benefits from learning a reward model as well. Instead of using the human demonstration data directly via supervised learning, we propose to leverage an Inverse Reinforcement Learning (IRL) technique to (explicitly or implicitly) build an reward model, while learning the policy model. This approach leads to new SFT algorithms that are not only efficient to implement, but also promote the ability to distinguish between the preferred and non-preferred continuations. Moreover, we identify a connection between the proposed IRL based approach, and certain self-play approach proposed recently, and showed that self-play is a special case of modeling a reward-learning agent. Theoretically, we show that the proposed algorithms converge to the stationary solutions of the IRL problem. Empirically, we align 1B and 7B models using proposed methods and evaluate them on a reward benchmark model and the HuggingFace Open LLM Leaderboard. The proposed methods show significant performance improvement over existing SFT approaches. Our results indicate that it is beneficial to explicitly or implicitly leverage reward learning throughout the entire alignment process.
Dual-Delayed Asynchronous SGD for Arbitrarily Heterogeneous Data
May 27, 2024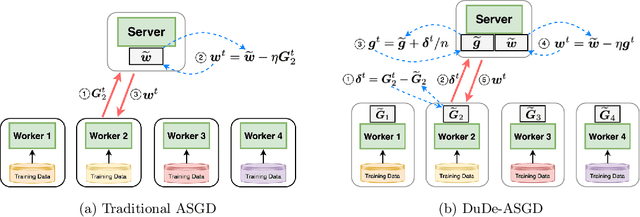

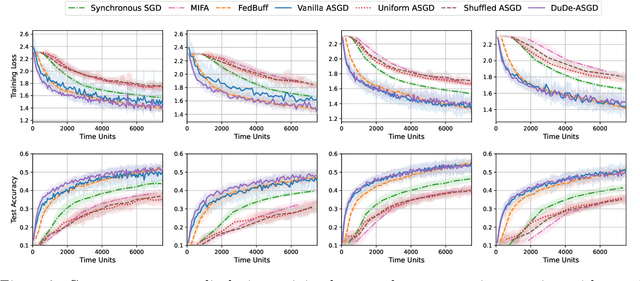
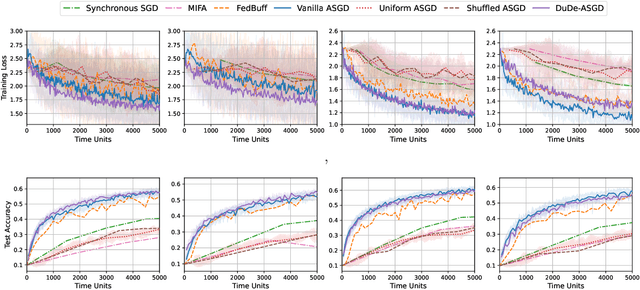
Abstract:We consider the distributed learning problem with data dispersed across multiple workers under the orchestration of a central server. Asynchronous Stochastic Gradient Descent (SGD) has been widely explored in such a setting to reduce the synchronization overhead associated with parallelization. However, the performance of asynchronous SGD algorithms often depends on a bounded dissimilarity condition among the workers' local data, a condition that can drastically affect their efficiency when the workers' data are highly heterogeneous. To overcome this limitation, we introduce the \textit{dual-delayed asynchronous SGD (DuDe-ASGD)} algorithm designed to neutralize the adverse effects of data heterogeneity. DuDe-ASGD makes full use of stale stochastic gradients from all workers during asynchronous training, leading to two distinct time lags in the model parameters and data samples utilized in the server's iterations. Furthermore, by adopting an incremental aggregation strategy, DuDe-ASGD maintains a per-iteration computational cost that is on par with traditional asynchronous SGD algorithms. Our analysis demonstrates that DuDe-ASGD achieves a near-minimax-optimal convergence rate for smooth nonconvex problems, even when the data across workers are extremely heterogeneous. Numerical experiments indicate that DuDe-ASGD compares favorably with existing asynchronous and synchronous SGD-based algorithms.
On Detecting Low-pass Graph Signals under Partial Observations
May 16, 2024Abstract:The application of graph signal processing (GSP) on partially observed graph signals with missing nodes has gained attention recently. This is because processing data from large graphs are difficult, if not impossible due to the lack of availability of full observations. Many prior works have been developed using the assumption that the generated graph signals are smooth or low pass filtered. This paper treats a blind graph filter detection problem under this context. We propose a detector that certifies whether the partially observed graph signals are low pass filtered, without requiring the graph topology knowledge. As an example application, our detector leads to a pre-screening method to filter out non low pass signals and thus robustify the prior GSP algorithms. We also bound the sample complexity of our detector in terms of the class of filters, number of observed nodes, etc. Numerical experiments verify the efficacy of our method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge