Clipped SGD Algorithms for Privacy Preserving Performative Prediction: Bias Amplification and Remedies
Paper and Code
Apr 17, 2024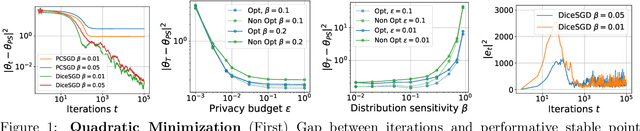

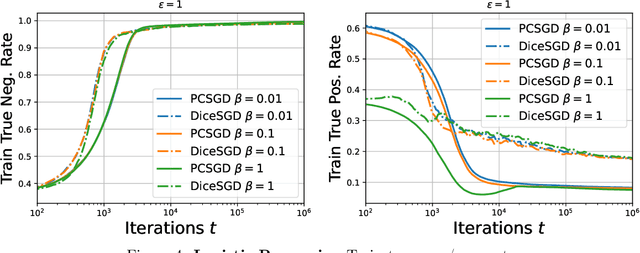
Clipped stochastic gradient descent (SGD) algorithms are among the most popular algorithms for privacy preserving optimization that reduces the leakage of users' identity in model training. This paper studies the convergence properties of these algorithms in a performative prediction setting, where the data distribution may shift due to the deployed prediction model. For example, the latter is caused by strategical users during the training of loan policy for banks. Our contributions are two-fold. First, we show that the straightforward implementation of a projected clipped SGD (PCSGD) algorithm may converge to a biased solution compared to the performative stable solution. We quantify the lower and upper bound for the magnitude of the bias and demonstrate a bias amplification phenomenon where the bias grows with the sensitivity of the data distribution. Second, we suggest two remedies to the bias amplification effect. The first one utilizes an optimal step size design for PCSGD that takes the privacy guarantee into account. The second one uses the recently proposed DiceSGD algorithm [Zhang et al., 2024]. We show that the latter can successfully remove the bias and converge to the performative stable solution. Numerical experiments verify our analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge