Dual-Delayed Asynchronous SGD for Arbitrarily Heterogeneous Data
Paper and Code
May 27, 2024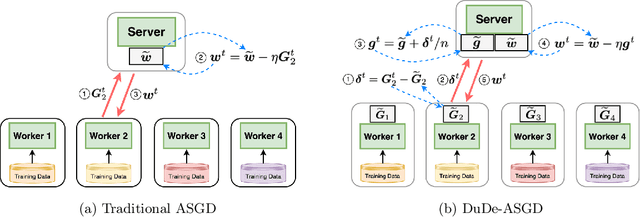

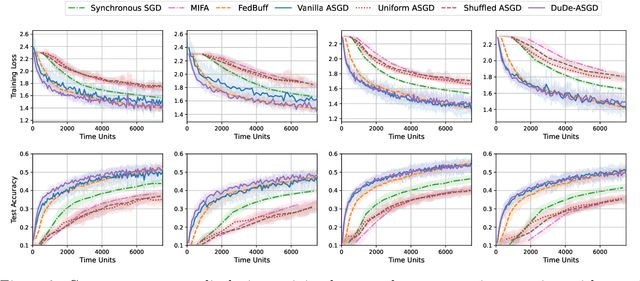
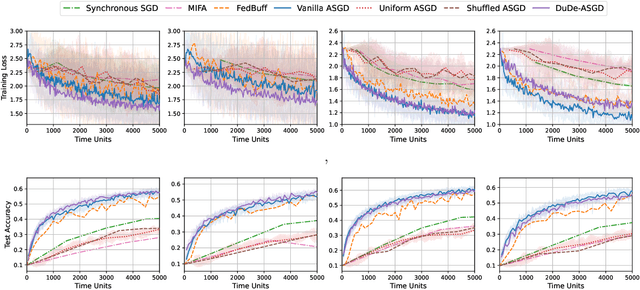
We consider the distributed learning problem with data dispersed across multiple workers under the orchestration of a central server. Asynchronous Stochastic Gradient Descent (SGD) has been widely explored in such a setting to reduce the synchronization overhead associated with parallelization. However, the performance of asynchronous SGD algorithms often depends on a bounded dissimilarity condition among the workers' local data, a condition that can drastically affect their efficiency when the workers' data are highly heterogeneous. To overcome this limitation, we introduce the \textit{dual-delayed asynchronous SGD (DuDe-ASGD)} algorithm designed to neutralize the adverse effects of data heterogeneity. DuDe-ASGD makes full use of stale stochastic gradients from all workers during asynchronous training, leading to two distinct time lags in the model parameters and data samples utilized in the server's iterations. Furthermore, by adopting an incremental aggregation strategy, DuDe-ASGD maintains a per-iteration computational cost that is on par with traditional asynchronous SGD algorithms. Our analysis demonstrates that DuDe-ASGD achieves a near-minimax-optimal convergence rate for smooth nonconvex problems, even when the data across workers are extremely heterogeneous. Numerical experiments indicate that DuDe-ASGD compares favorably with existing asynchronous and synchronous SGD-based algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge