Xiaolu Wang
Exponential Topology-enabled Scalable Communication in Multi-agent Reinforcement Learning
Feb 27, 2025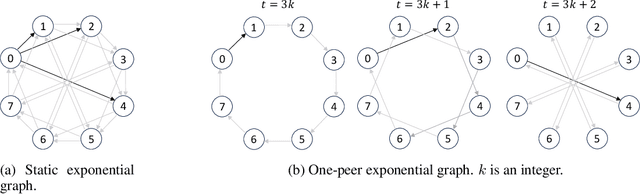
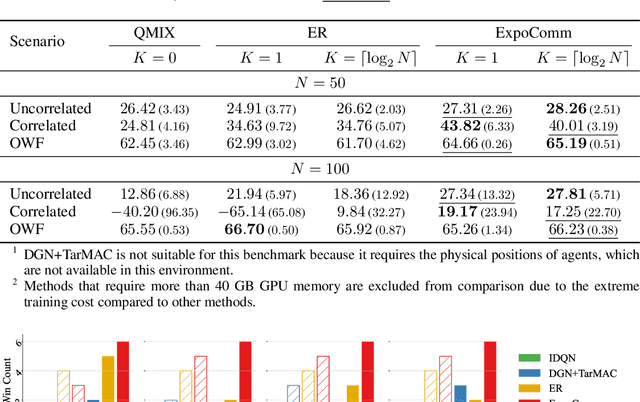
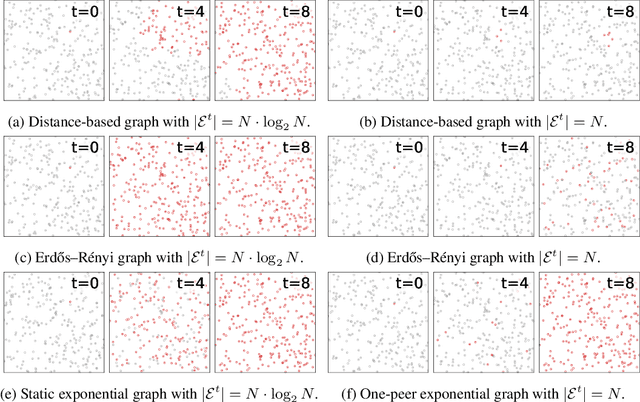
Abstract:In cooperative multi-agent reinforcement learning (MARL), well-designed communication protocols can effectively facilitate consensus among agents, thereby enhancing task performance. Moreover, in large-scale multi-agent systems commonly found in real-world applications, effective communication plays an even more critical role due to the escalated challenge of partial observability compared to smaller-scale setups. In this work, we endeavor to develop a scalable communication protocol for MARL. Unlike previous methods that focus on selecting optimal pairwise communication links-a task that becomes increasingly complex as the number of agents grows-we adopt a global perspective on communication topology design. Specifically, we propose utilizing the exponential topology to enable rapid information dissemination among agents by leveraging its small-diameter and small-size properties. This approach leads to a scalable communication protocol, named ExpoComm. To fully unlock the potential of exponential graphs as communication topologies, we employ memory-based message processors and auxiliary tasks to ground messages, ensuring that they reflect global information and benefit decision-making. Extensive experiments on large-scale cooperative benchmarks, including MAgent and Infrastructure Management Planning, demonstrate the superior performance and robust zero-shot transferability of ExpoComm compared to existing communication strategies. The code is publicly available at https://github.com/LXXXXR/ExpoComm.
SAFL: Structure-Aware Personalized Federated Learning via Client-Specific Clustering and SCSI-Guided Model Pruning
Jan 30, 2025



Abstract:Federated Learning (FL) enables clients to collaboratively train machine learning models without sharing local data, preserving privacy in diverse environments. While traditional FL approaches preserve privacy, they often struggle with high computational and communication overhead. To address these issues, model pruning is introduced as a strategy to streamline computations. However, existing pruning methods, when applied solely based on local data, often produce sub-models that inadequately reflect clients' specific tasks due to data insufficiency. To overcome these challenges, this paper introduces SAFL (Structure-Aware Federated Learning), a novel framework that enhances personalized federated learning through client-specific clustering and Similar Client Structure Information (SCSI)-guided model pruning. SAFL employs a two-stage process: initially, it groups clients based on data similarities and uses aggregated pruning criteria to guide the pruning process, facilitating the identification of optimal sub-models. Subsequently, clients train these pruned models and engage in server-based aggregation, ensuring tailored and efficient models for each client. This method significantly reduces computational overhead while improving inference accuracy. Extensive experiments demonstrate that SAFL markedly diminishes model size and improves performance, making it highly effective in federated environments characterized by heterogeneous data.
Dual-Delayed Asynchronous SGD for Arbitrarily Heterogeneous Data
May 27, 2024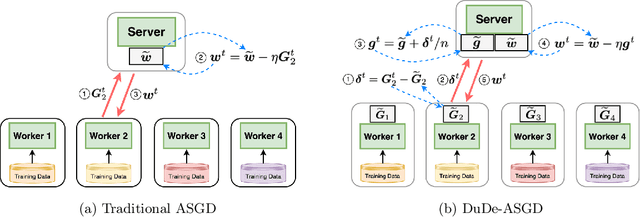

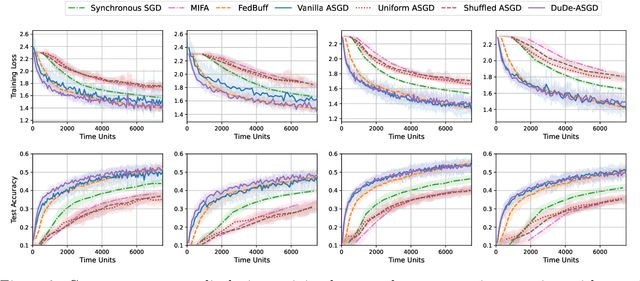
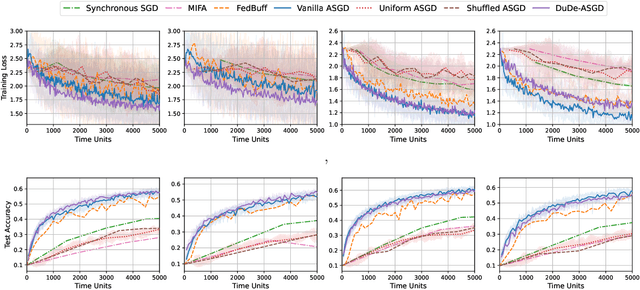
Abstract:We consider the distributed learning problem with data dispersed across multiple workers under the orchestration of a central server. Asynchronous Stochastic Gradient Descent (SGD) has been widely explored in such a setting to reduce the synchronization overhead associated with parallelization. However, the performance of asynchronous SGD algorithms often depends on a bounded dissimilarity condition among the workers' local data, a condition that can drastically affect their efficiency when the workers' data are highly heterogeneous. To overcome this limitation, we introduce the \textit{dual-delayed asynchronous SGD (DuDe-ASGD)} algorithm designed to neutralize the adverse effects of data heterogeneity. DuDe-ASGD makes full use of stale stochastic gradients from all workers during asynchronous training, leading to two distinct time lags in the model parameters and data samples utilized in the server's iterations. Furthermore, by adopting an incremental aggregation strategy, DuDe-ASGD maintains a per-iteration computational cost that is on par with traditional asynchronous SGD algorithms. Our analysis demonstrates that DuDe-ASGD achieves a near-minimax-optimal convergence rate for smooth nonconvex problems, even when the data across workers are extremely heterogeneous. Numerical experiments indicate that DuDe-ASGD compares favorably with existing asynchronous and synchronous SGD-based algorithms.
Achieving Linear Speedup in Asynchronous Federated Learning with Heterogeneous Clients
Feb 17, 2024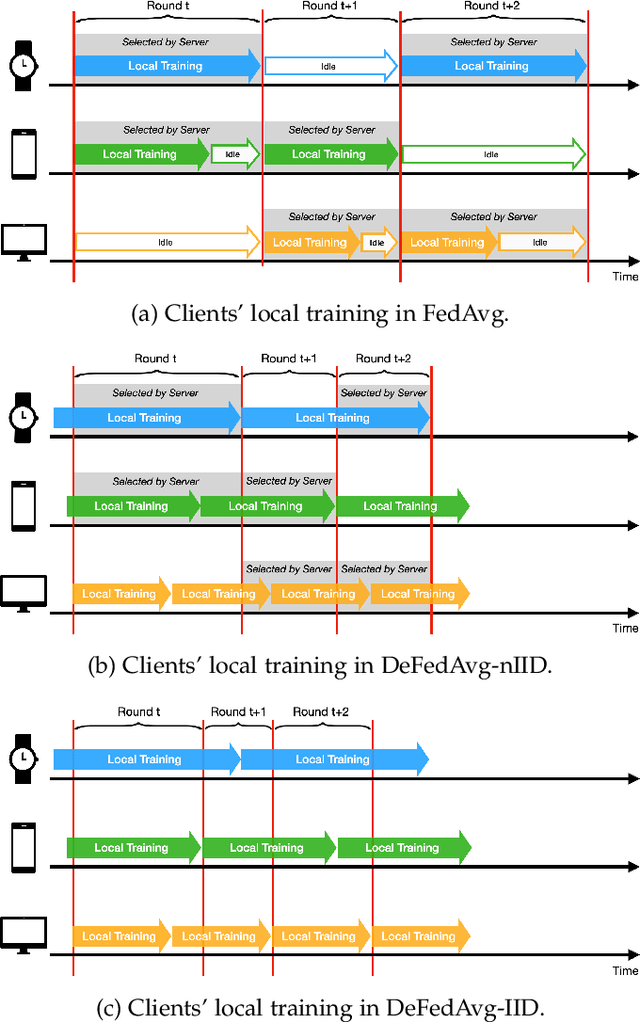
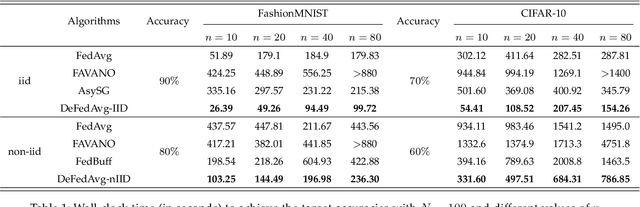
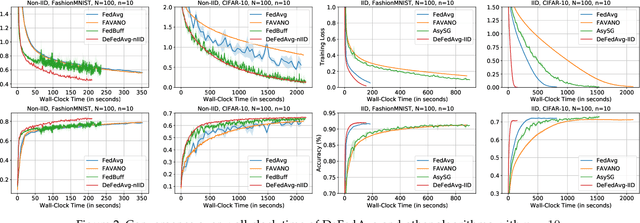
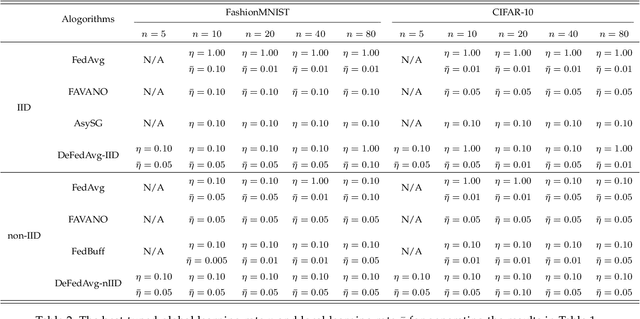
Abstract:Federated learning (FL) is an emerging distributed training paradigm that aims to learn a common global model without exchanging or transferring the data that are stored locally at different clients. The Federated Averaging (FedAvg)-based algorithms have gained substantial popularity in FL to reduce the communication overhead, where each client conducts multiple localized iterations before communicating with a central server. In this paper, we focus on FL where the clients have diverse computation and/or communication capabilities. Under this circumstance, FedAvg can be less efficient since it requires all clients that participate in the global aggregation in a round to initiate iterations from the latest global model, and thus the synchronization among fast clients and straggler clients can severely slow down the overall training process. To address this issue, we propose an efficient asynchronous federated learning (AFL) framework called Delayed Federated Averaging (DeFedAvg). In DeFedAvg, the clients are allowed to perform local training with different stale global models at their own paces. Theoretical analyses demonstrate that DeFedAvg achieves asymptotic convergence rates that are on par with the results of FedAvg for solving nonconvex problems. More importantly, DeFedAvg is the first AFL algorithm that provably achieves the desirable linear speedup property, which indicates its high scalability. Additionally, we carry out extensive numerical experiments using real datasets to validate the efficiency and scalability of our approach when training deep neural networks.
Linear Speedup of Incremental Aggregated Gradient Methods on Streaming Data
Sep 10, 2023Abstract:This paper considers a type of incremental aggregated gradient (IAG) method for large-scale distributed optimization. The IAG method is well suited for the parameter server architecture as the latter can easily aggregate potentially staled gradients contributed by workers. Although the convergence of IAG in the case of deterministic gradient is well known, there are only a few results for the case of its stochastic variant based on streaming data. Considering strongly convex optimization, this paper shows that the streaming IAG method achieves linear speedup when the workers are updating frequently enough, even if the data sample distribution across workers are heterogeneous. We show that the expected squared distance to optimal solution decays at O((1+T)/(nt)), where $n$ is the number of workers, t is the iteration number, and T/n is the update frequency of workers. Our analysis involves careful treatments of the conditional expectations with staled gradients and a recursive system with both delayed and noise terms, which are new to the analysis of IAG-type algorithms. Numerical results are presented to verify our findings.
* 8 pages, 3 figures
Automatic tagging of knowledge points for K12 math problems
Aug 21, 2022

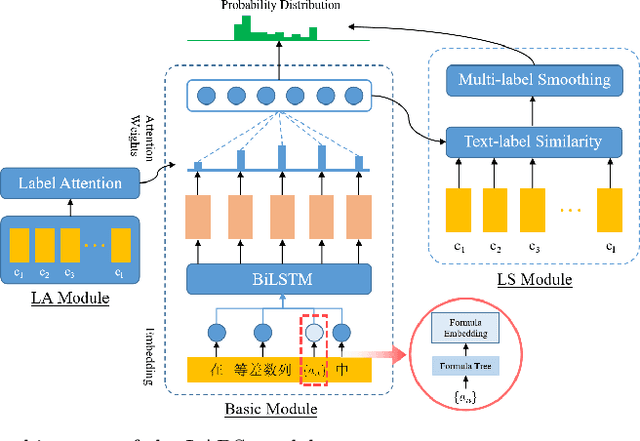
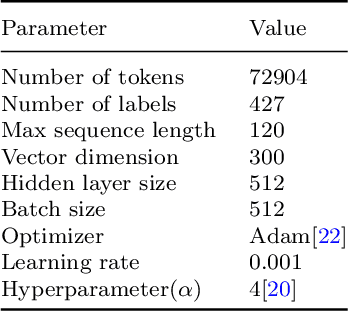
Abstract:Automatic tagging of knowledge points for practice problems is the basis for managing question bases and improving the automation and intelligence of education. Therefore, it is of great practical significance to study the automatic tagging technology for practice problems. However, there are few studies on the automatic tagging of knowledge points for math problems. Math texts have more complex structures and semantics compared with general texts because they contain unique elements such as symbols and formulas. Therefore, it is difficult to meet the accuracy requirement of knowledge point prediction by directly applying the text classification techniques in general domains. In this paper, K12 math problems taken as the research object, the LABS model based on label-semantic attention and multi-label smoothing combining textual features is proposed to improve the automatic tagging of knowledge points for math problems. The model combines the text classification techniques in general domains and the unique features of math texts. The results show that the models using label-semantic attention or multi-label smoothing perform better on precision, recall, and F1-score metrics than the traditional BiLSTM model, while the LABS model using both performs best. It can be seen that label information can guide the neural networks to extract meaningful information from the problem text, which improves the text classification performance of the model. Moreover, multi-label smoothing combining textual features can fully explore the relationship between text and labels, improve the model's prediction ability for new data and improve the model's classification accuracy.
Exact Community Recovery over Signed Graphs
Feb 22, 2022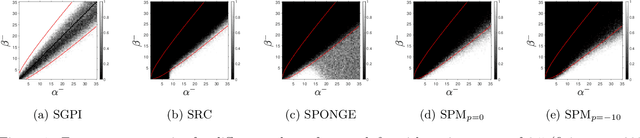
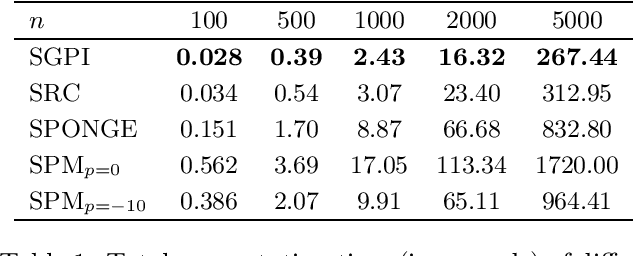

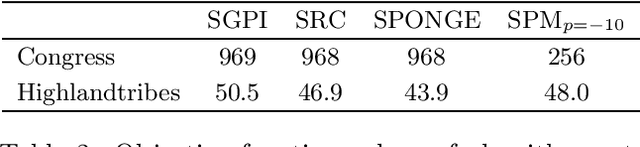
Abstract:Signed graphs encode similarity and dissimilarity relationships among different entities with positive and negative edges. In this paper, we study the problem of community recovery over signed graphs generated by the signed stochastic block model (SSBM) with two equal-sized communities. Our approach is based on the maximum likelihood estimation (MLE) of the SSBM. Unlike many existing approaches, our formulation reveals that the positive and negative edges of a signed graph should be treated unequally. We then propose a simple two-stage iterative algorithm for solving the regularized MLE. It is shown that in the logarithmic degree regime, the proposed algorithm can exactly recover the underlying communities in nearly-linear time at the information-theoretic limit. Numerical results on both synthetic and real data are reported to validate and complement our theoretical developments and demonstrate the efficacy of the proposed method.
Learning Graphs from Smooth Signals under Moment Uncertainty
May 12, 2021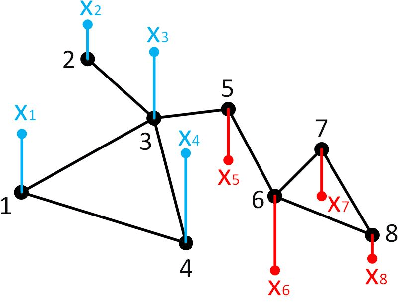
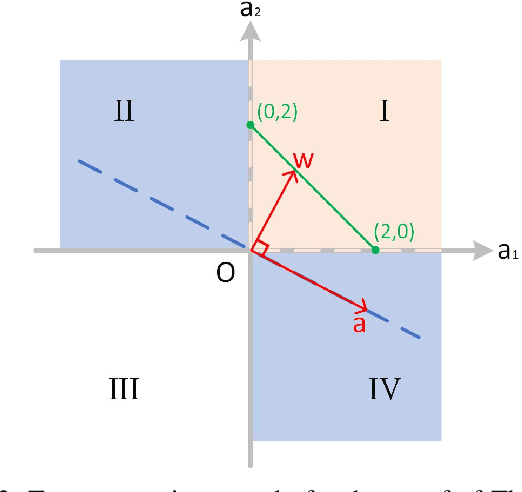
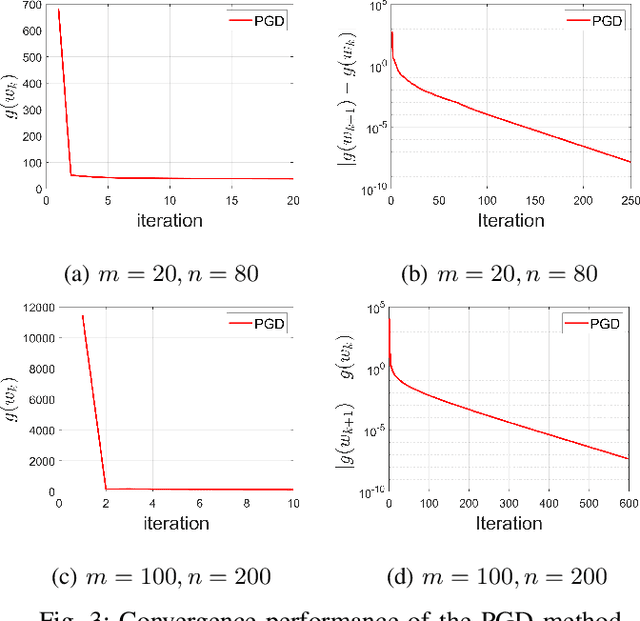

Abstract:We consider the problem of inferring the graph structure from a given set of smooth graph signals. The number of perceived graph signals is always finite and possibly noisy, thus the statistical properties of the data distribution is ambiguous. Traditional graph learning models do not take this distributional uncertainty into account, thus performance may be sensitive to different sets of data. In this paper, we propose a distributionally robust approach to graph learning, which incorporates the first and second moment uncertainty into the smooth graph learning model. Specifically, we cast our graph learning model as a minimax optimization problem, and further reformulate it as a nonconvex minimization problem with linear constraints. In our proposed formulation, we find a theoretical interpretation of the Laplacian regularizer, which is adopted in many existing works in an intuitive manner. Although the first moment uncertainty leads to an annoying square root term in the objective function, we prove that it enjoys the smoothness property with probability 1 over the entire constraint. We develop a efficient projected gradient descent (PGD) method and establish its global iterate convergence to a critical point. We conduct extensive experiments on both synthetic and real data to verify the effectiveness of our model and the efficiency of the PGD algorithm. Compared with the state-of-the-art smooth graph learning methods, our approach exhibits superior and more robust performance across different populations of signals in terms of various evaluation metrics.
Interactive Visual Exploration of Topic Models using Graphs
Nov 27, 2014
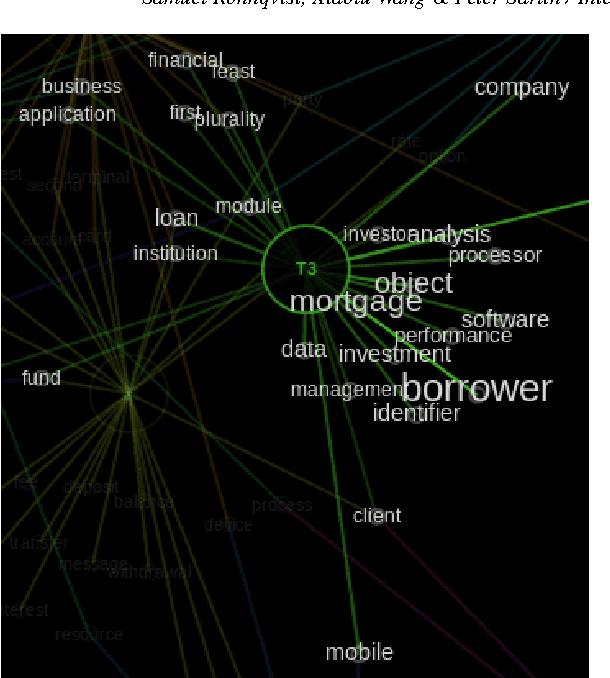
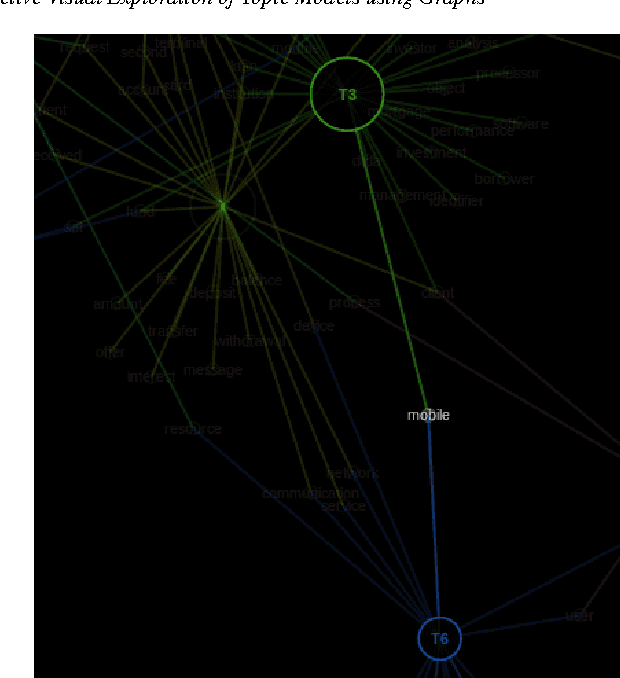
Abstract:Probabilistic topic modeling is a popular and powerful family of tools for uncovering thematic structure in large sets of unstructured text documents. While much attention has been directed towards the modeling algorithms and their various extensions, comparatively few studies have concerned how to present or visualize topic models in meaningful ways. In this paper, we present a novel design that uses graphs to visually communicate topic structure and meaning. By connecting topic nodes via descriptive keyterms, the graph representation reveals topic similarities, topic meaning and shared, ambiguous keyterms. At the same time, the graph can be used for information retrieval purposes, to find documents by topic or topic subsets. To exemplify the utility of the design, we illustrate its use for organizing and exploring corpora of financial patents.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge