Yuen-Man Pun
Schedulers for Schedule-free: Theoretically inspired hyperparameters
Nov 11, 2025Abstract:The recently proposed schedule-free method has been shown to achieve strong performance when hyperparameter tuning is limited. The current theory for schedule-free only supports a constant learning rate, where-as the implementation used in practice uses a warm-up schedule. We show how to extend the last-iterate convergence theory of schedule-free to allow for any scheduler, and how the averaging parameter has to be updated as a function of the learning rate. We then perform experiments showing how our convergence theory has some predictive power with regards to practical executions on deep neural networks, despite that this theory relies on assuming convexity. When applied to the warmup-stable-decay (wsd) schedule, our theory shows the optimal convergence rate of $\mathcal{O}(1/\sqrt{T})$. We then use convexity to design a new adaptive Polyak learning rate schedule for schedule-free. We prove an optimal anytime last-iterate convergence for our new Polyak schedule, and show that it performs well compared to a number of baselines on a black-box model distillation task.
Minimisation of Quasar-Convex Functions Using Random Zeroth-Order Oracles
May 04, 2025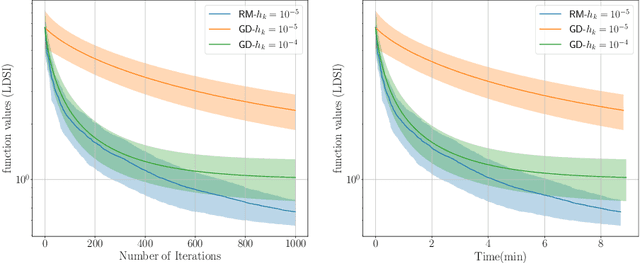
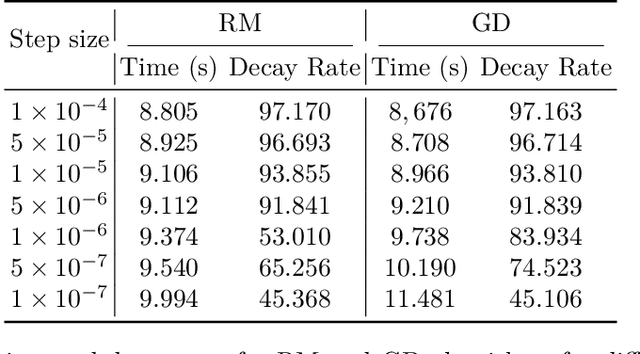
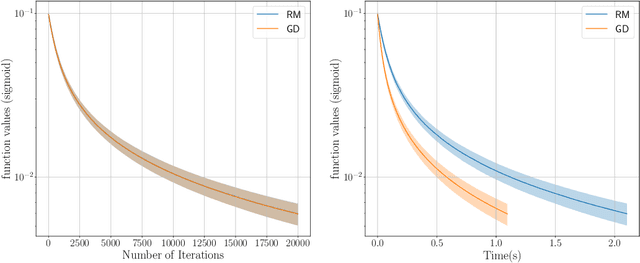
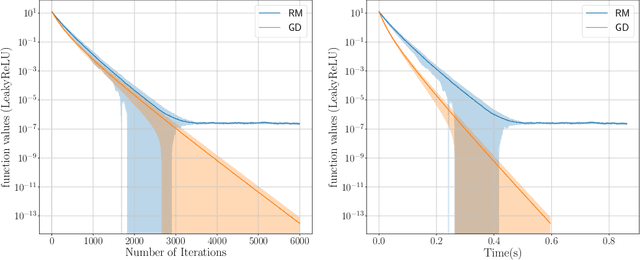
Abstract:This study explores the performance of a random Gaussian smoothing zeroth-order (ZO) scheme for minimising quasar-convex (QC) and strongly quasar-convex (SQC) functions in both unconstrained and constrained settings. For the unconstrained problem, we establish the ZO algorithm's convergence to a global minimum along with its complexity when applied to both QC and SQC functions. For the constrained problem, we introduce the new notion of proximal-quasar-convexity and prove analogous results to the unconstrained case. Specifically, we show the complexity bounds and the convergence of the algorithm to a neighbourhood of a global minimum whose size can be controlled under a variance reduction scheme. Theoretical findings are illustrated through investigating the performance of the algorithm applied to a range of problems in machine learning and optimisation. Specifically, we observe scenarios where the ZO method outperforms gradient descent. We provide a possible explanation for this phenomenon.
Properties of Fixed Points of Generalised Extra Gradient Methods Applied to Min-Max Problems
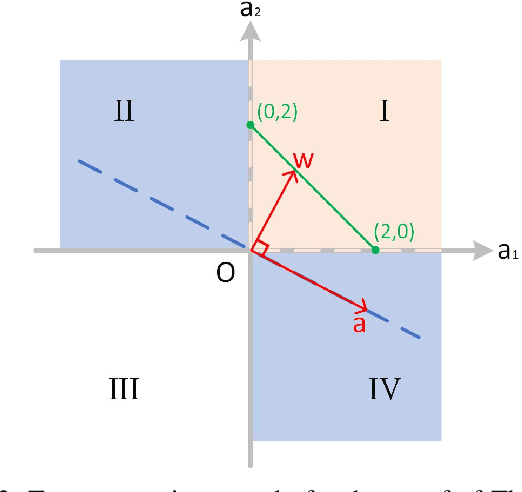
Apr 03, 2025Abstract:This paper studies properties of fixed points of generalised Extra-gradient (GEG) algorithms applied to min-max problems. We discuss connections between saddle points of the objective function of the min-max problem and GEG fixed points. We show that, under appropriate step-size selections, the set of saddle points (Nash equilibria) is a subset of stable fixed points of GEG. Convergence properties of the GEG algorithm are obtained through a stability analysis of a discrete-time dynamical system. The results and benefits when compared to existing methods are illustrated through numerical examples.
Online Non-Stationary Stochastic Quasar-Convex Optimization
Jul 04, 2024

Abstract:Recent research has shown that quasar-convexity can be found in applications such as identification of linear dynamical systems and generalized linear models. Such observations have in turn spurred exciting developments in design and analysis algorithms that exploit quasar-convexity. In this work, we study the online stochastic quasar-convex optimization problems in a dynamic environment. We establish regret bounds of online gradient descent in terms of cumulative path variation and cumulative gradient variance for losses satisfying quasar-convexity and strong quasar-convexity. We then apply the results to generalized linear models (GLM) when the underlying parameter is time-varying. We establish regret bounds of online gradient descent when applying to GLMs with leaky ReLU activation function, logistic activation function, and ReLU activation function. Numerical results are presented to corroborate our findings.
Distributionally Time-Varying Online Stochastic Optimization under Polyak-Łojasiewicz Condition with Application in Conditional Value-at-Risk Statistical Learning
Sep 18, 2023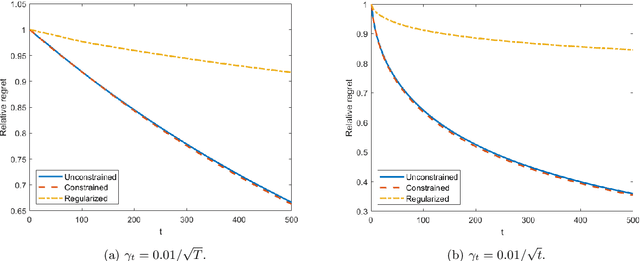
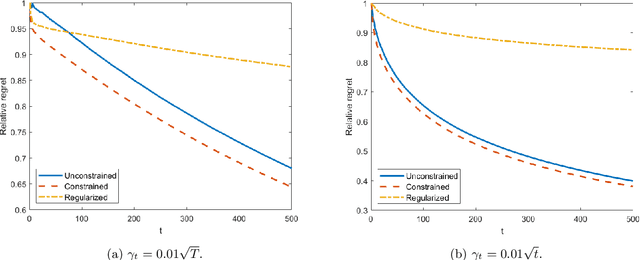
Abstract:In this work, we consider a sequence of stochastic optimization problems following a time-varying distribution via the lens of online optimization. Assuming that the loss function satisfies the Polyak-{\L}ojasiewicz condition, we apply online stochastic gradient descent and establish its dynamic regret bound that is composed of cumulative distribution drifts and cumulative gradient biases caused by stochasticity. The distribution metric we adopt here is Wasserstein distance, which is well-defined without the absolute continuity assumption or with a time-varying support set. We also establish a regret bound of online stochastic proximal gradient descent when the objective function is regularized. Moreover, we show that the above framework can be applied to the Conditional Value-at-Risk (CVaR) learning problem. Particularly, we improve an existing proof on the discovery of the PL condition of the CVaR problem, resulting in a regret bound of online stochastic gradient descent.
Local Strong Convexity of Source Localization and Error Bound for Target Tracking under Time-of-Arrival Measurements
Dec 21, 2021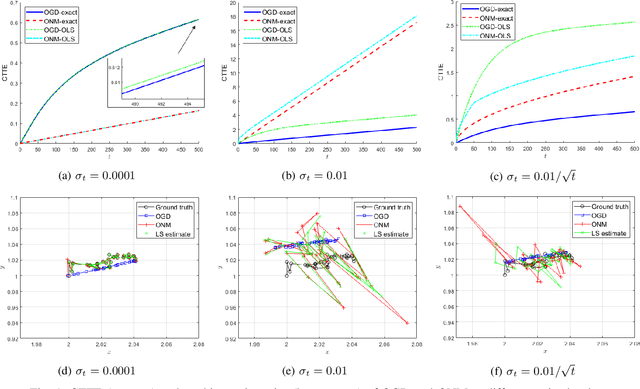
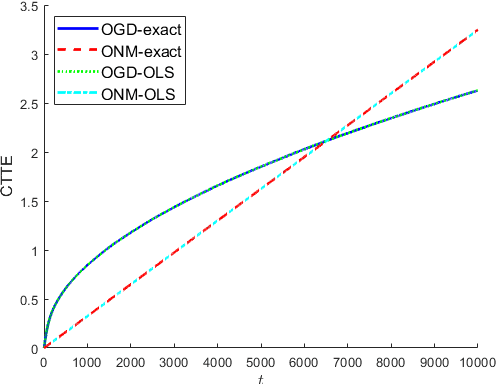
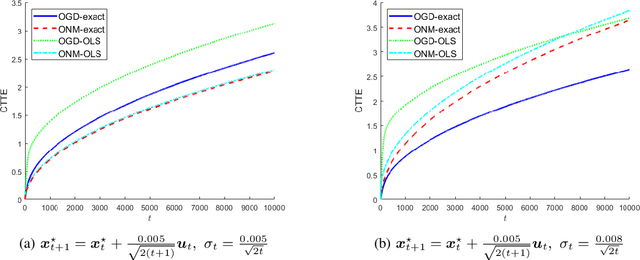
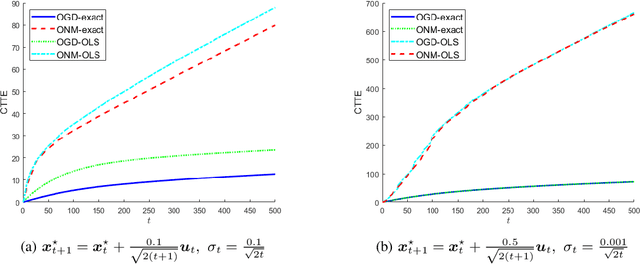
Abstract:In this paper, we consider a time-varying optimization approach to the problem of tracking a moving target using noisy time-of-arrival (TOA) measurements. Specifically, we formulate the problem as that of sequential TOA-based source localization and apply online gradient descent (OGD) to it to generate the position estimates of the target. To analyze the tracking performance of OGD, we first revisit the classic least-squares formulation of the (static) TOA-based source localization problem and elucidate its estimation and geometric properties. In particular, under standard assumptions on the TOA measurement model, we establish a bound on the distance between an optimal solution to the least-squares formulation and the true target position. Using this bound, we show that the loss function in the formulation, albeit non-convex in general, is locally strongly convex at its global minima. To the best of our knowledge, these results are new and can be of independent interest. By combining them with existing techniques from online strongly convex optimization, we then establish the first non-trivial bound on the cumulative target tracking error of OGD. Our numerical results corroborate the theoretical findings and show that OGD can effectively track the target at different noise levels.
Learning Graphs from Smooth Signals under Moment Uncertainty
May 12, 2021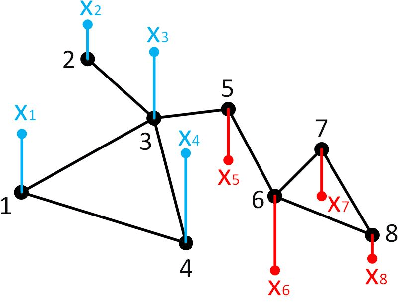
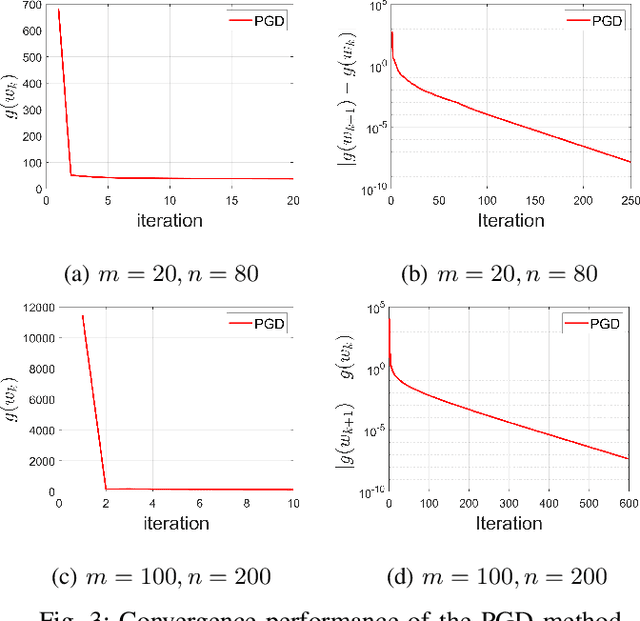

Abstract:We consider the problem of inferring the graph structure from a given set of smooth graph signals. The number of perceived graph signals is always finite and possibly noisy, thus the statistical properties of the data distribution is ambiguous. Traditional graph learning models do not take this distributional uncertainty into account, thus performance may be sensitive to different sets of data. In this paper, we propose a distributionally robust approach to graph learning, which incorporates the first and second moment uncertainty into the smooth graph learning model. Specifically, we cast our graph learning model as a minimax optimization problem, and further reformulate it as a nonconvex minimization problem with linear constraints. In our proposed formulation, we find a theoretical interpretation of the Laplacian regularizer, which is adopted in many existing works in an intuitive manner. Although the first moment uncertainty leads to an annoying square root term in the objective function, we prove that it enjoys the smoothness property with probability 1 over the entire constraint. We develop a efficient projected gradient descent (PGD) method and establish its global iterate convergence to a critical point. We conduct extensive experiments on both synthetic and real data to verify the effectiveness of our model and the efficiency of the PGD algorithm. Compared with the state-of-the-art smooth graph learning methods, our approach exhibits superior and more robust performance across different populations of signals in terms of various evaluation metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge