Distributionally Time-Varying Online Stochastic Optimization under Polyak-Łojasiewicz Condition with Application in Conditional Value-at-Risk Statistical Learning
Paper and Code
Sep 18, 2023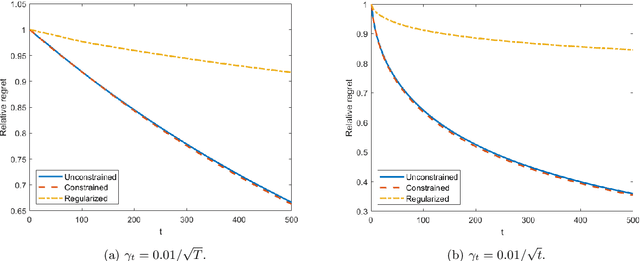
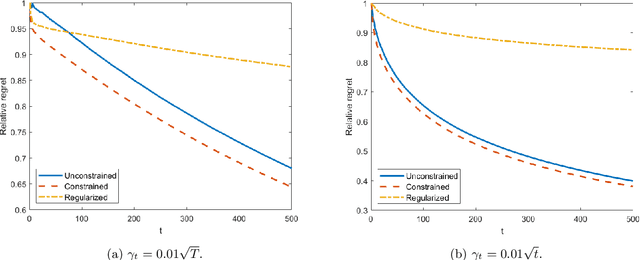
In this work, we consider a sequence of stochastic optimization problems following a time-varying distribution via the lens of online optimization. Assuming that the loss function satisfies the Polyak-{\L}ojasiewicz condition, we apply online stochastic gradient descent and establish its dynamic regret bound that is composed of cumulative distribution drifts and cumulative gradient biases caused by stochasticity. The distribution metric we adopt here is Wasserstein distance, which is well-defined without the absolute continuity assumption or with a time-varying support set. We also establish a regret bound of online stochastic proximal gradient descent when the objective function is regularized. Moreover, we show that the above framework can be applied to the Conditional Value-at-Risk (CVaR) learning problem. Particularly, we improve an existing proof on the discovery of the PL condition of the CVaR problem, resulting in a regret bound of online stochastic gradient descent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge