Optimal Universal Quantum Encoding for Statistical Inference

Optimal encoding of classical data for statistical inference using quantum computing is investigated. A universal encoder is sought that is optimal for a wide array of statistical inference tasks. Accuracy of any statistical inference is shown to be upper bounded by a term that is proportional to maximal quantum leakage from the classical data, i.e., the input to the inference model, through its quantum encoding. This demonstrates that the maximal quantum leakage is a universal measure of the quality of the encoding strategy for statistical inference as it only depends on the quantum encoding of the data and not the inference task itself. The optimal universal encoding strategy, i.e., the encoding strategy that maximizes the maximal quantum leakage, is proved to be attained by pure states. When there are enough qubits, basis encoding is proved to be universally optimal. An iterative method for numerically computing the optimal universal encoding strategy is presented.

Information Leakage from Data Updates in Machine Learning Models

In this paper we consider the setting where machine learning models are retrained on updated datasets in order to incorporate the most up-to-date information or reflect distribution shifts. We investigate whether one can infer information about these updates in the training data (e.g., changes to attribute values of records). Here, the adversary has access to snapshots of the machine learning model before and after the change in the dataset occurs. Contrary to the existing literature, we assume that an attribute of a single or multiple training data points are changed rather than entire data records are removed or added. We propose attacks based on the difference in the prediction confidence of the original model and the updated model. We evaluate our attack methods on two public datasets along with multi-layer perceptron and logistic regression models. We validate that two snapshots of the model can result in higher information leakage in comparison to having access to only the updated model. Moreover, we observe that data records with rare values are more vulnerable to attacks, which points to the disparate vulnerability of privacy attacks in the update setting. When multiple records with the same original attribute value are updated to the same new value (i.e., repeated changes), the attacker is more likely to correctly guess the updated values since repeated changes leave a larger footprint on the trained model. These observations point to vulnerability of machine learning models to attribute inference attacks in the update setting.

Distributionally Time-Varying Online Stochastic Optimization under Polyak-Łojasiewicz Condition with Application in Conditional Value-at-Risk Statistical Learning

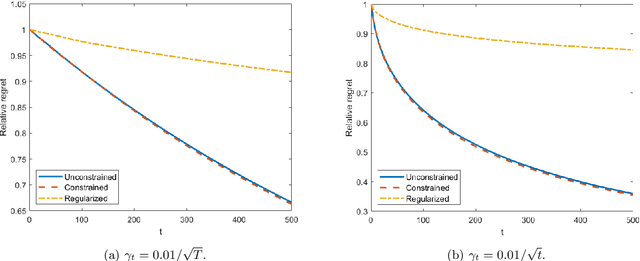
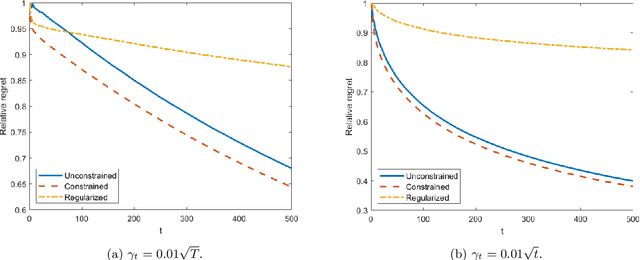
In this work, we consider a sequence of stochastic optimization problems following a time-varying distribution via the lens of online optimization. Assuming that the loss function satisfies the Polyak-{\L}ojasiewicz condition, we apply online stochastic gradient descent and establish its dynamic regret bound that is composed of cumulative distribution drifts and cumulative gradient biases caused by stochasticity. The distribution metric we adopt here is Wasserstein distance, which is well-defined without the absolute continuity assumption or with a time-varying support set. We also establish a regret bound of online stochastic proximal gradient descent when the objective function is regularized. Moreover, we show that the above framework can be applied to the Conditional Value-at-Risk (CVaR) learning problem. Particularly, we improve an existing proof on the discovery of the PL condition of the CVaR problem, resulting in a regret bound of online stochastic gradient descent.

Distributionally-Robust Optimization with Noisy Data for Discrete Uncertainties Using Total Variation Distance

Stochastic programs where the uncertainty distribution must be inferred from noisy data samples are considered. The stochastic programs are approximated with distributionally-robust optimizations that minimize the worst-case expected cost over ambiguity sets, i.e., sets of distributions that are sufficiently compatible with the observed data. In this paper, the ambiguity sets capture the set of probability distributions whose convolution with the noise distribution remains within a ball centered at the empirical noisy distribution of data samples parameterized by the total variation distance. Using the prescribed ambiguity set, the solutions of the distributionally-robust optimizations converge to the solutions of the original stochastic programs when the numbers of the data samples grow to infinity. Therefore, the proposed distributionally-robust optimization problems are asymptotically consistent. This is proved under the assumption that the distribution of the noise is uniformly diagonally dominant. More importantly, the distributionally-robust optimization problems can be cast as tractable convex optimization problems and are therefore amenable to large-scale stochastic problems.

Safe Learning of Linear Time-Invariant Systems

We consider safety in simultaneous learning and control of discrete-time linear time-invariant systems. We provide rigorous confidence bounds on the learned model of the system based on the number of utilized state measurements. These bounds are used to modify control inputs to the system via an optimization problem with potentially time-varying safety constraints. We prove that the state can only exit the safe set with small probability, provided a feasible solution to the safety-constrained optimization exists. This optimization problem is then reformulated in a more computationally-friendly format by tightening the safety constraints to account for model uncertainty during learning. The tightening decreases as the confidence in the learned model improves. We finally prove that, under persistence of excitation, the tightening becomes negligible as more measurements are gathered.

Optimal Stochastic Evasive Maneuvers Using the Schrodinger's Equation

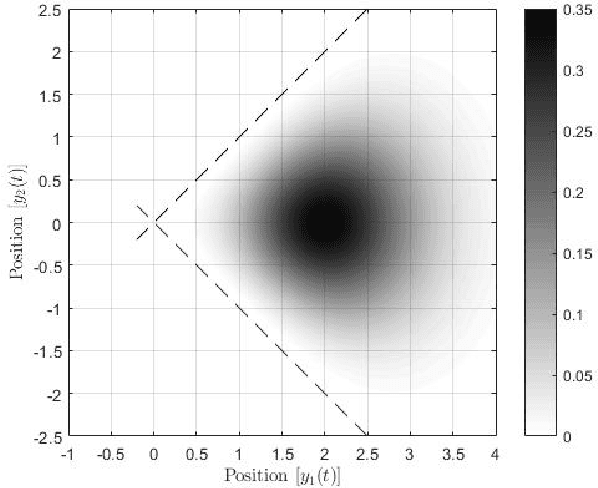
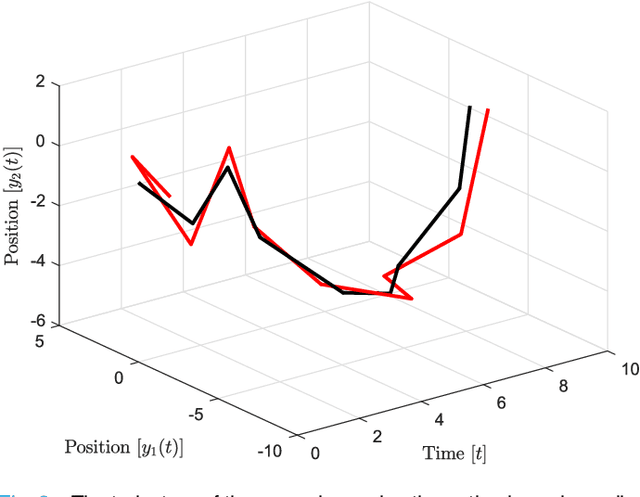
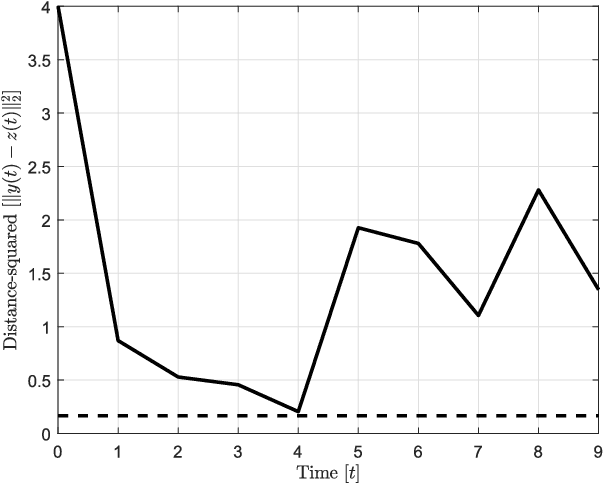
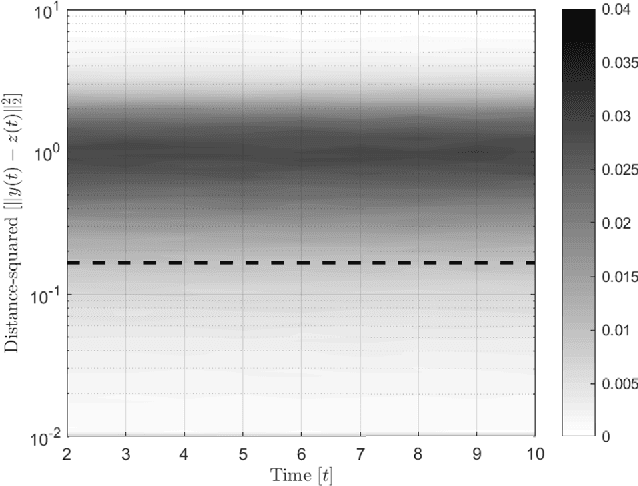
In this paper, preys with stochastic evasion policies are considered. The stochasticity adds unpredictable changes to the prey's path for avoiding predator's attacks. The prey's cost function is composed of two terms balancing the unpredictability factor (by using stochasticity to make the task of forecasting its future positions by the predator difficult) and energy consumption (the least amount of energy required for performing a maneuver). The optimal probability density functions of the actions of the prey for trading-off unpredictability and energy consumption is shown to be characterized by the stationary Schrodinger's equation.

Safe Learning of Uncertain Environments for Nonlinear Control-Affine Systems

In many learning based control methodologies, learning the unknown dynamic model precedes the control phase, while the aim is to control the system such that it remains in some safe region of the state space. In this work our aim is to guarantee safety while learning and control proceed simultaneously. Specifically, we consider the problem of safe learning in nonlinear control-affine systems subject to unknown additive uncertainty. We model uncertainty as a Gaussian signal and use state measurements to learn its mean and covariance. We provide rigorous time-varying bounds on the mean and covariance of the uncertainty and employ them to modify the control input via an optimisation program with safety constraints encoded as a barrier function on the state space. We show that with an arbitrarily large probability we can guarantee that the state will remain in the safe set, while learning and control are carried out simultaneously, provided that a feasible solution exists for the optimisation problem. We provide a secondary formulation of this optimisation that is computationally more efficient. This is based on tightening the safety constraints to counter the uncertainty about the learned mean and covariance. The magnitude of the tightening can be decreased as our confidence in the learned mean and covariance increases (i.e., as we gather more measurements about the environment). Extensions of the method are provided for Gaussian uncertainties with piecewise constant mean and covariance to accommodate more general environments.

Optimal Pre-Processing to Achieve Fairness and Its Relationship with Total Variation Barycenter

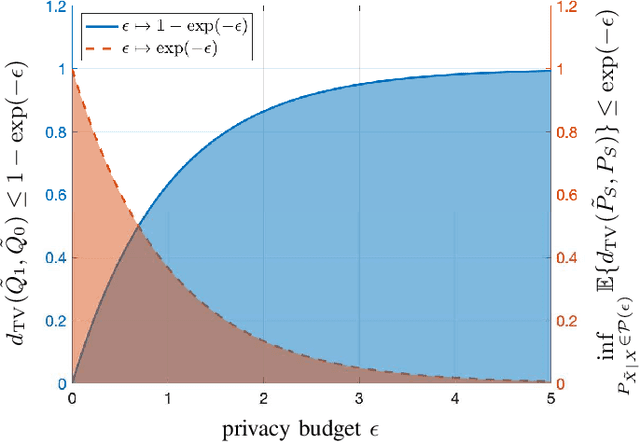
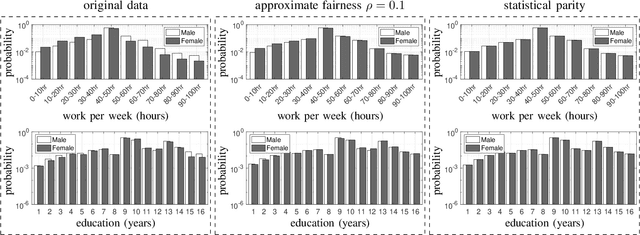
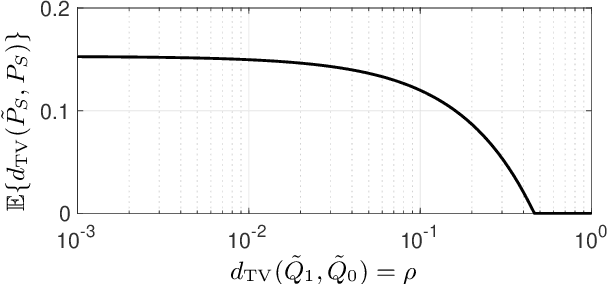
We use disparate impact, i.e., the extent that the probability of observing an output depends on protected attributes such as race and gender, to measure fairness. We prove that disparate impact is upper bounded by the total variation distance between the distribution of the inputs given the protected attributes. We then use pre-processing, also known as data repair, to enforce fairness. We show that utility degradation, i.e., the extent that the success of a forecasting model changes by pre-processing the data, is upper bounded by the total variation distance between the distribution of the data before and after pre-processing. Hence, the problem of finding the optimal pre-processing regiment for enforcing fairness can be cast as minimizing total variations distance between the distribution of the data before and after pre-processing subject to a constraint on the total variation distance between the distribution of the inputs given protected attributes. This problem is a linear program that can be efficiently solved. We show that this problem is intimately related to finding the barycenter (i.e., center of mass) of two distributions when distances in the probability space are measured by total variation distance. We also investigate the effect of differential privacy on fairness using the proposed the total variation distances. We demonstrate the results using numerical experimentation with a practice dataset.

Gradient Sparsification Can Improve Performance of Differentially-Private Convex Machine Learning

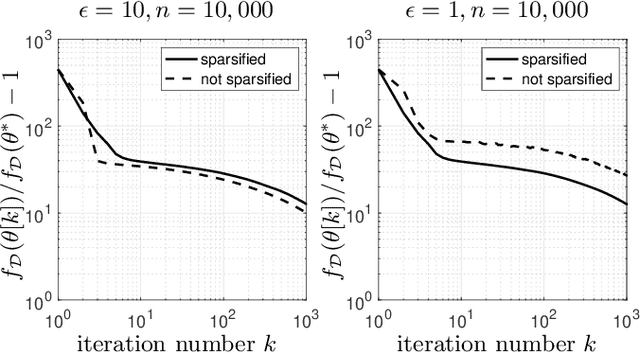
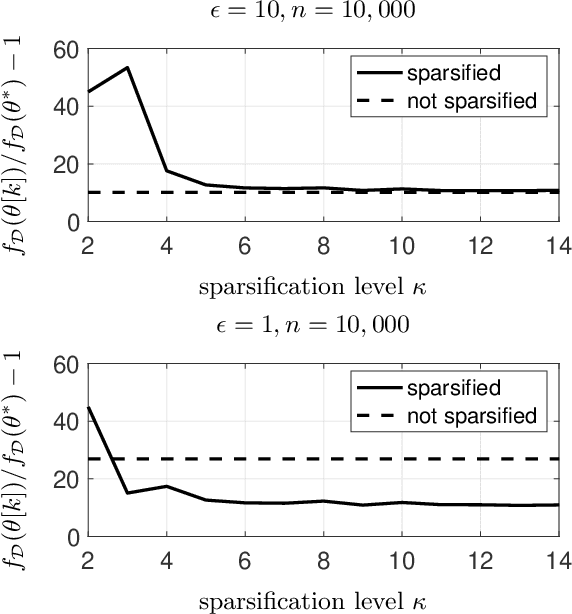
We use gradient sparsification to reduce the adverse effect of differential privacy noise on performance of private machine learning models. To this aim, we employ compressed sensing and additive Laplace noise to evaluate differentially-private gradients. Noisy privacy-preserving gradients are used to perform stochastic gradient descent for training machine learning models. Sparsification, achieved by setting the smallest gradient entries to zero, can reduce the convergence speed of the training algorithm. However, by sparsification and compressed sensing, the dimension of communicated gradient and the magnitude of additive noise can be reduced. The interplay between these effects determines whether gradient sparsification improves the performance of differentially-private machine learning models. We investigate this analytically in the paper. We prove that, for small privacy budgets, compression can improve performance of privacy-preserving machine learning models. However, for large privacy budgets, compression does not necessarily improve the performance. Intuitively, this is because the effect of privacy-preserving noise is minimal in large privacy budget regime and thus improvements from gradient sparsification cannot compensate for its slower convergence.

When Machine Learning Meets Privacy: A Survey and Outlook

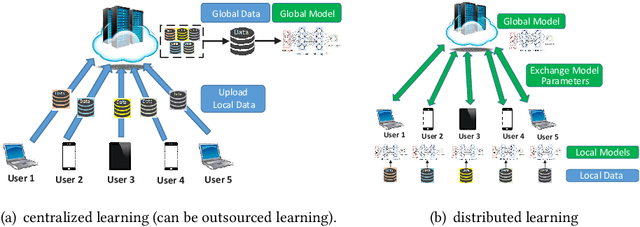
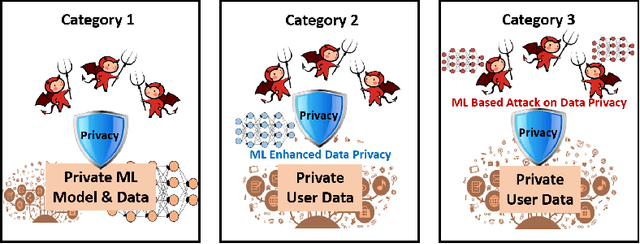
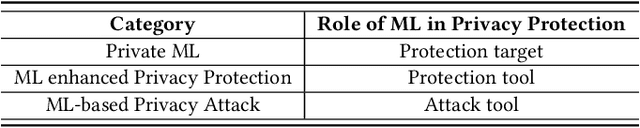
The newly emerged machine learning (e.g. deep learning) methods have become a strong driving force to revolutionize a wide range of industries, such as smart healthcare, financial technology, and surveillance systems. Meanwhile, privacy has emerged as a big concern in this machine learning-based artificial intelligence era. It is important to note that the problem of privacy preservation in the context of machine learning is quite different from that in traditional data privacy protection, as machine learning can act as both friend and foe. Currently, the work on the preservation of privacy and machine learning (ML) is still in an infancy stage, as most existing solutions only focus on privacy problems during the machine learning process. Therefore, a comprehensive study on the privacy preservation problems and machine learning is required. This paper surveys the state of the art in privacy issues and solutions for machine learning. The survey covers three categories of interactions between privacy and machine learning: (i) private machine learning, (ii) machine learning aided privacy protection, and (iii) machine learning-based privacy attack and corresponding protection schemes. The current research progress in each category is reviewed and the key challenges are identified. Finally, based on our in-depth analysis of the area of privacy and machine learning, we point out future research directions in this field.