Optimal Pre-Processing to Achieve Fairness and Its Relationship with Total Variation Barycenter
Paper and Code
Jan 18, 2021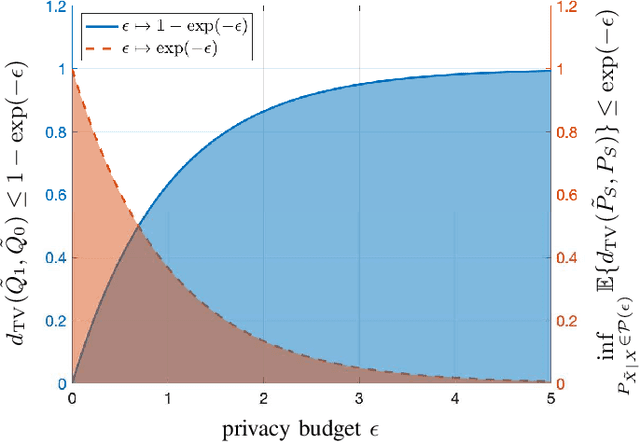
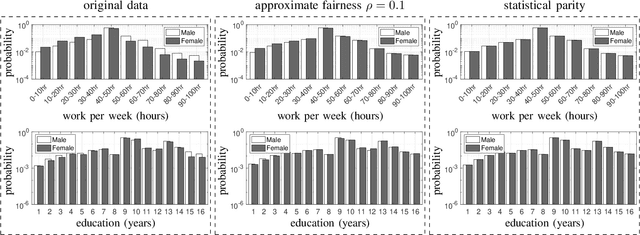
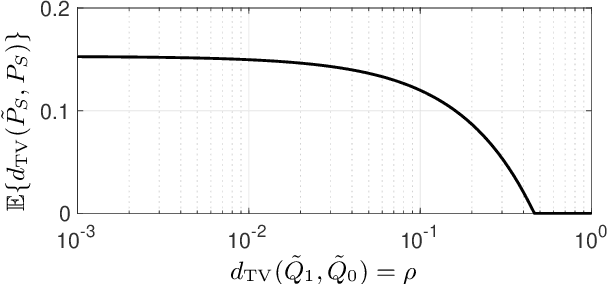
We use disparate impact, i.e., the extent that the probability of observing an output depends on protected attributes such as race and gender, to measure fairness. We prove that disparate impact is upper bounded by the total variation distance between the distribution of the inputs given the protected attributes. We then use pre-processing, also known as data repair, to enforce fairness. We show that utility degradation, i.e., the extent that the success of a forecasting model changes by pre-processing the data, is upper bounded by the total variation distance between the distribution of the data before and after pre-processing. Hence, the problem of finding the optimal pre-processing regiment for enforcing fairness can be cast as minimizing total variations distance between the distribution of the data before and after pre-processing subject to a constraint on the total variation distance between the distribution of the inputs given protected attributes. This problem is a linear program that can be efficiently solved. We show that this problem is intimately related to finding the barycenter (i.e., center of mass) of two distributions when distances in the probability space are measured by total variation distance. We also investigate the effect of differential privacy on fairness using the proposed the total variation distances. We demonstrate the results using numerical experimentation with a practice dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge