Gradient Sparsification Can Improve Performance of Differentially-Private Convex Machine Learning
Paper and Code
Dec 01, 2020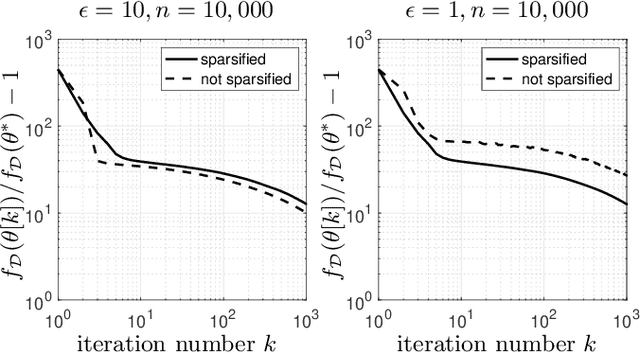
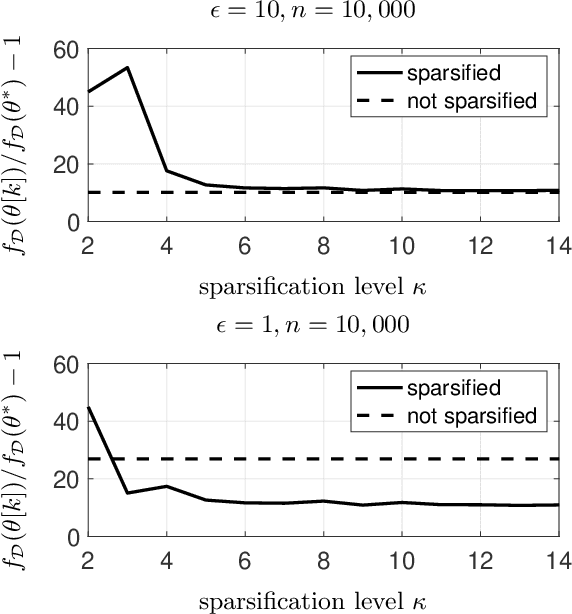
We use gradient sparsification to reduce the adverse effect of differential privacy noise on performance of private machine learning models. To this aim, we employ compressed sensing and additive Laplace noise to evaluate differentially-private gradients. Noisy privacy-preserving gradients are used to perform stochastic gradient descent for training machine learning models. Sparsification, achieved by setting the smallest gradient entries to zero, can reduce the convergence speed of the training algorithm. However, by sparsification and compressed sensing, the dimension of communicated gradient and the magnitude of additive noise can be reduced. The interplay between these effects determines whether gradient sparsification improves the performance of differentially-private machine learning models. We investigate this analytically in the paper. We prove that, for small privacy budgets, compression can improve performance of privacy-preserving machine learning models. However, for large privacy budgets, compression does not necessarily improve the performance. Intuitively, this is because the effect of privacy-preserving noise is minimal in large privacy budget regime and thus improvements from gradient sparsification cannot compensate for its slower convergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge