Solving the Offline and Online Min-Max Problem of Non-smooth Submodular-Concave Functions: A Zeroth-Order Approach

We consider max-min and min-max problems with objective functions that are possibly non-smooth, submodular with respect to the minimiser and concave with respect to the maximiser. We investigate the performance of a zeroth-order method applied to this problem. The method is based on the subgradient of the Lovász extension of the objective function with respect to the minimiser and based on Gaussian smoothing to estimate the smoothed function gradient with respect to the maximiser. In expectation sense, we prove the convergence of the algorithm to an $ε$-saddle point in the offline case. Moreover, we show that, in the expectation sense, in the online setting, the algorithm achieves $O(\sqrt{N\bar{P}_N})$ online duality gap, where $N$ is the number of iterations and $\bar{P}_N$ is the path length of the sequence of optimal decisions. The complexity analysis and hyperparameter selection are presented for all the cases. The theoretical results are illustrated via numerical examples.

Minimisation of Quasar-Convex Functions Using Random Zeroth-Order Oracles

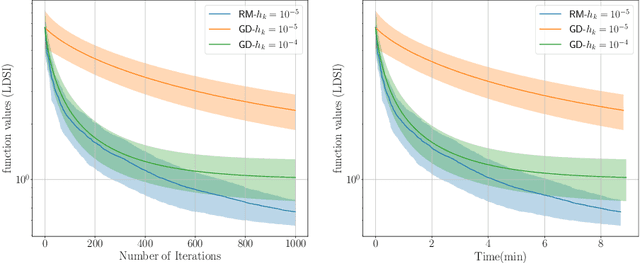
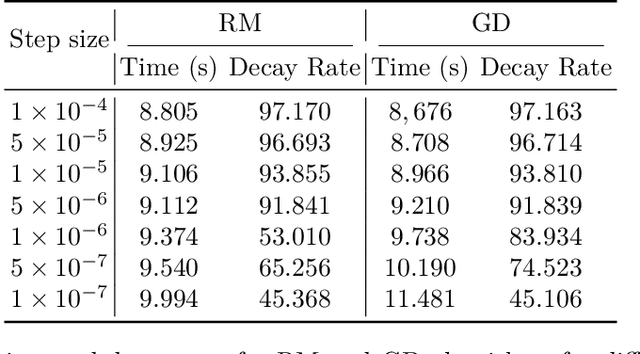
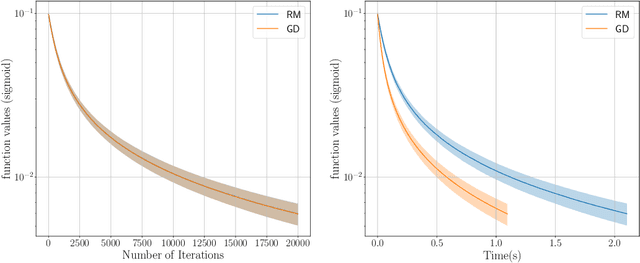
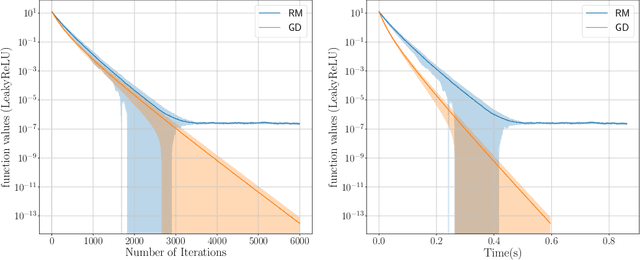
This study explores the performance of a random Gaussian smoothing zeroth-order (ZO) scheme for minimising quasar-convex (QC) and strongly quasar-convex (SQC) functions in both unconstrained and constrained settings. For the unconstrained problem, we establish the ZO algorithm's convergence to a global minimum along with its complexity when applied to both QC and SQC functions. For the constrained problem, we introduce the new notion of proximal-quasar-convexity and prove analogous results to the unconstrained case. Specifically, we show the complexity bounds and the convergence of the algorithm to a neighbourhood of a global minimum whose size can be controlled under a variance reduction scheme. Theoretical findings are illustrated through investigating the performance of the algorithm applied to a range of problems in machine learning and optimisation. Specifically, we observe scenarios where the ZO method outperforms gradient descent. We provide a possible explanation for this phenomenon.

Min-Max Optimisation for Nonconvex-Nonconcave Functions Using a Random Zeroth-Order Extragradient Algorithm

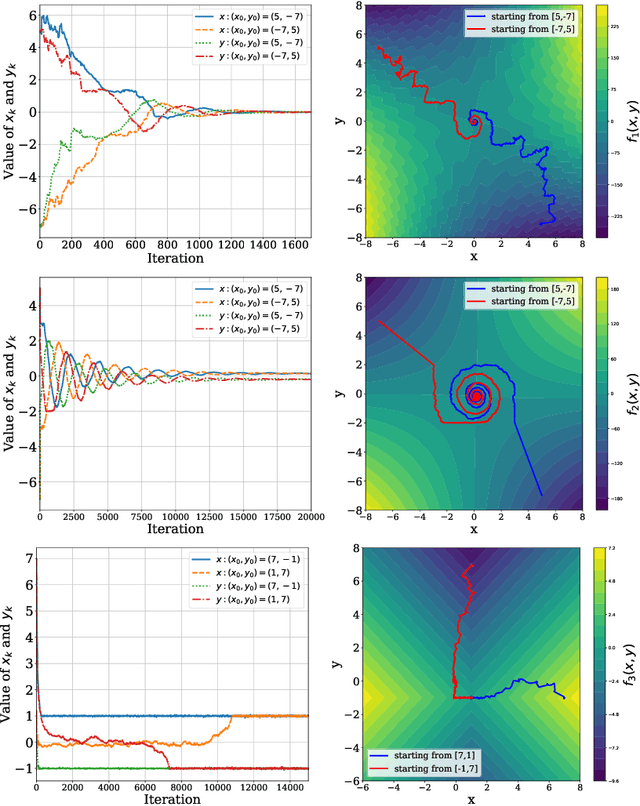
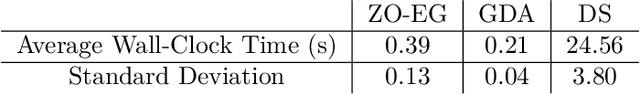
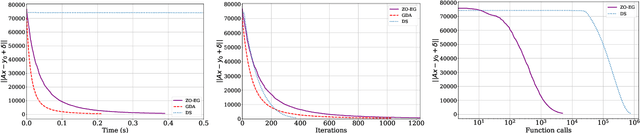
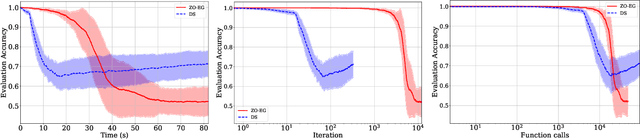
This study explores the performance of the random Gaussian smoothing Zeroth-Order ExtraGradient (ZO-EG) scheme considering min-max optimisation problems with possibly NonConvex-NonConcave (NC-NC) objective functions. We consider both unconstrained and constrained, differentiable and non-differentiable settings. We discuss the min-max problem from the point of view of variational inequalities. For the unconstrained problem, we establish the convergence of the ZO-EG algorithm to the neighbourhood of an $\epsilon$-stationary point of the NC-NC objective function, whose radius can be controlled under a variance reduction scheme, along with its complexity. For the constrained problem, we introduce the new notion of proximal variational inequalities and give examples of functions satisfying this property. Moreover, we prove analogous results to the unconstrained case for the constrained problem. For the non-differentiable case, we prove the convergence of the ZO-EG algorithm to a neighbourhood of an $\epsilon$-stationary point of the smoothed version of the objective function, where the radius of the neighbourhood can be controlled, which can be related to the ($\delta,\epsilon$)-Goldstein stationary point of the original objective function.

Properties of Fixed Points of Generalised Extra Gradient Methods Applied to Min-Max Problems

This paper studies properties of fixed points of generalised Extra-gradient (GEG) algorithms applied to min-max problems. We discuss connections between saddle points of the objective function of the min-max problem and GEG fixed points. We show that, under appropriate step-size selections, the set of saddle points (Nash equilibria) is a subset of stable fixed points of GEG. Convergence properties of the GEG algorithm are obtained through a stability analysis of a discrete-time dynamical system. The results and benefits when compared to existing methods are illustrated through numerical examples.

Minimisation of Polyak-Łojasewicz Functions Using Random Zeroth-Order Oracles

The application of a zeroth-order scheme for minimising Polyak-\L{}ojasewicz (PL) functions is considered. The framework is based on exploiting a random oracle to estimate the function gradient. The convergence of the algorithm to a global minimum in the unconstrained case and to a neighbourhood of the global minimum in the constrained case along with their corresponding complexity bounds are presented. The theoretical results are demonstrated via numerical examples.