Regularized infill criteria for multi-objective Bayesian optimization with application to aircraft design

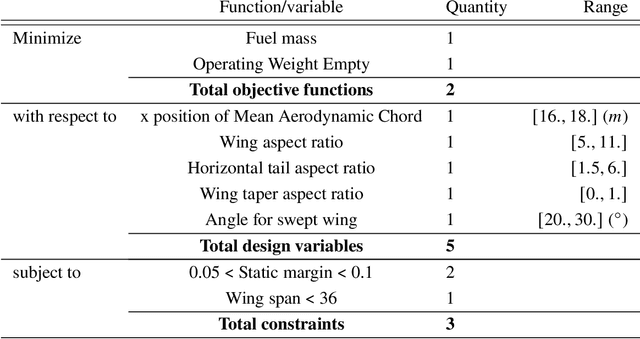
Bayesian optimization is an advanced tool to perform ecient global optimization It consists on enriching iteratively surrogate Kriging models of the objective and the constraints both supposed to be computationally expensive of the targeted optimization problem Nowadays efficient extensions of Bayesian optimization to solve expensive multiobjective problems are of high interest The proposed method in this paper extends the super efficient global optimization with mixture of experts SEGOMOE to solve constrained multiobjective problems To cope with the illposedness of the multiobjective inll criteria different enrichment procedures using regularization techniques are proposed The merit of the proposed approaches are shown on known multiobjective benchmark problems with and without constraints The proposed methods are then used to solve a biobjective application related to conceptual aircraft design with ve unknown design variables and three nonlinear inequality constraints The preliminary results show a reduction of the total cost in terms of function evaluations by a factor of 20 compared to the evolutionary algorithm NSGA-II.

Bayesian optimization for mixed variables using an adaptive dimension reduction process: applications to aircraft design

Multidisciplinary design optimization methods aim at adapting numerical optimization techniques to the design of engineering systems involving multiple disciplines. In this context, a large number of mixed continuous, integer and categorical variables might arise during the optimization process and practical applications involve a large number of design variables. Recently, there has been a growing interest in mixed variables constrained Bayesian optimization but most existing approaches severely increase the number of the hyperparameters related to the surrogate model. In this paper, we address this issue by constructing surrogate models using less hyperparameters. The reduction process is based on the partial least squares method. An adaptive procedure for choosing the number of hyperparameters is proposed. The performance of the proposed approach is confirmed on analytical tests as well as two real applications related to aircraft design. A significant improvement is obtained compared to genetic algorithms.

Min-Max Optimisation for Nonconvex-Nonconcave Functions Using a Random Zeroth-Order Extragradient Algorithm

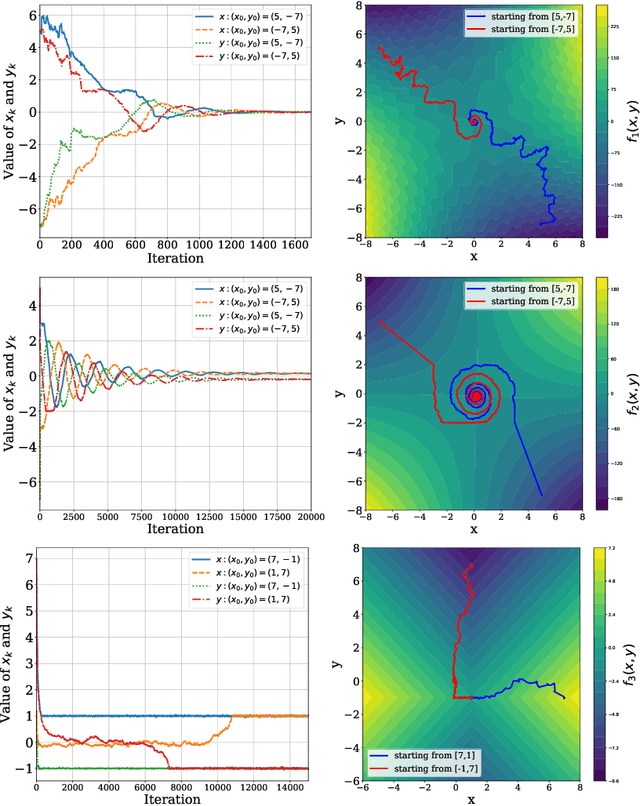
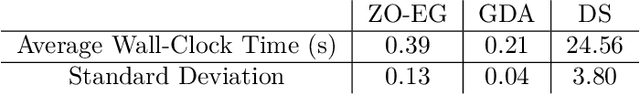
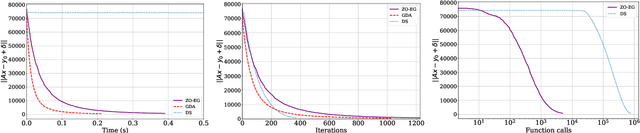
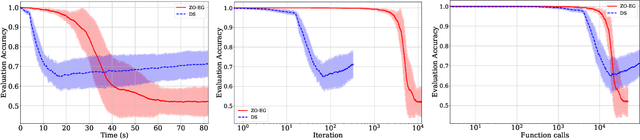
This study explores the performance of the random Gaussian smoothing Zeroth-Order ExtraGradient (ZO-EG) scheme considering min-max optimisation problems with possibly NonConvex-NonConcave (NC-NC) objective functions. We consider both unconstrained and constrained, differentiable and non-differentiable settings. We discuss the min-max problem from the point of view of variational inequalities. For the unconstrained problem, we establish the convergence of the ZO-EG algorithm to the neighbourhood of an $\epsilon$-stationary point of the NC-NC objective function, whose radius can be controlled under a variance reduction scheme, along with its complexity. For the constrained problem, we introduce the new notion of proximal variational inequalities and give examples of functions satisfying this property. Moreover, we prove analogous results to the unconstrained case for the constrained problem. For the non-differentiable case, we prove the convergence of the ZO-EG algorithm to a neighbourhood of an $\epsilon$-stationary point of the smoothed version of the objective function, where the radius of the neighbourhood can be controlled, which can be related to the ($\delta,\epsilon$)-Goldstein stationary point of the original objective function.

A Proximal Modified Quasi-Newton Method for Nonsmooth Regularized Optimization

We develop R2N, a modified quasi-Newton method for minimizing the sum of a $\mathcal{C}^1$ function $f$ and a lower semi-continuous prox-bounded $h$. Both $f$ and $h$ may be nonconvex. At each iteration, our method computes a step by minimizing the sum of a quadratic model of $f$, a model of $h$, and an adaptive quadratic regularization term. A step may be computed by a variant of the proximal-gradient method. An advantage of R2N over trust-region (TR) methods is that proximal operators do not involve an extra TR indicator. We also develop the variant R2DH, in which the model Hessian is diagonal, which allows us to compute a step without relying on a subproblem solver when $h$ is separable. R2DH can be used as standalone solver, but also as subproblem solver inside R2N. We describe non-monotone variants of both R2N and R2DH. Global convergence of a first-order stationarity measure to zero holds without relying on local Lipschitz continuity of $\nabla f$, while allowing model Hessians to grow unbounded, an assumption particularly relevant to quasi-Newton models. Under Lipschitz-continuity of $\nabla f$, we establish a tight worst-case complexity bound of $O(1 / \epsilon^{2/(1 - p)})$ to bring said measure below $\epsilon > 0$, where $0 \leq p < 1$ controls the growth of model Hessians. The latter must not diverge faster than $|\mathcal{S}_k|^p$, where $\mathcal{S}_k$ is the set of successful iterations up to iteration $k$. When $p = 1$, we establish the tight exponential complexity bound $O(\exp(c \epsilon^{-2}))$ where $c > 0$ is a constant. We describe our Julia implementation and report numerical experience on a basis-pursuit problem, image denoising, minimum-rank matrix completion, and a nonlinear support vector machine. In particular, the minimum-rank problem cannot be solved directly at this time by a TR approach as corresponding proximal operators are not known analytically.

A graph-structured distance for heterogeneous datasets with meta variables

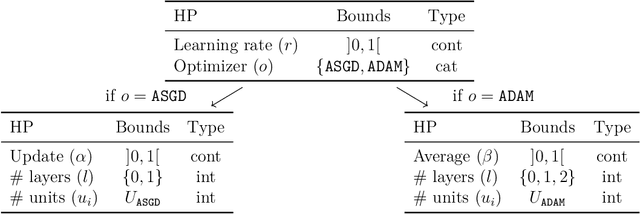
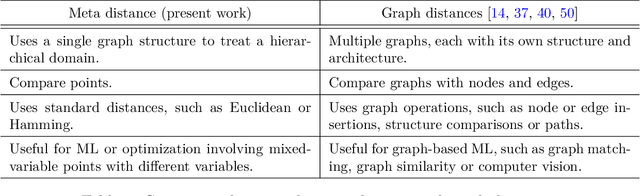
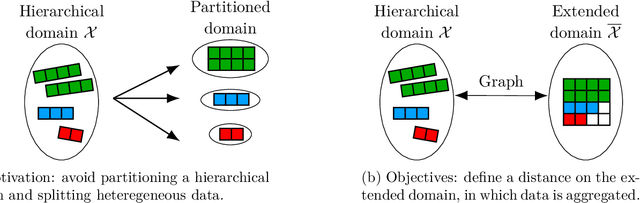
Heterogeneous datasets emerge in various machine learning or optimization applications that feature different data sources, various data types and complex relationships between variables. In practice, heterogeneous datasets are often partitioned into smaller well-behaved ones that are easier to process. However, some applications involve expensive-to-generate or limited size datasets, which motivates methods based on the whole dataset. The first main contribution of this work is a modeling graph-structured framework that generalizes state-of-the-art hierarchical, tree-structured, or variable-size frameworks. This framework models domains that involve heterogeneous datasets in which variables may be continuous, integer, or categorical, with some identified as meta if their values determine the inclusion/exclusion or affect the bounds of other so-called decreed variables. Excluded variables are introduced to manage variables that are either included or excluded depending on the given points. The second main contribution is the graph-structured distance that compares extended points with any combination of included and excluded variables: any pair of points can be compared, allowing to work directly in heterogeneous datasets with meta variables. The contributions are illustrated with some regression experiments, in which the performance of a multilayer perceptron with respect to its hyperparameters is modeled with inverse distance weighting and $K$-nearest neighbors models.

A general error analysis for randomized low-rank approximation with application to data assimilation

Randomized algorithms have proven to perform well on a large class of numerical linear algebra problems. Their theoretical analysis is critical to provide guarantees on their behaviour, and in this sense, the stochastic analysis of the randomized low-rank approximation error plays a central role. Indeed, several randomized methods for the approximation of dominant eigen- or singular modes can be rewritten as low-rank approximation methods. However, despite the large variety of algorithms, the existing theoretical frameworks for their analysis rely on a specific structure for the covariance matrix that is not adapted to all the algorithms. We propose a general framework for the stochastic analysis of the low-rank approximation error in Frobenius norm for centered and non-standard Gaussian matrices. Under minimal assumptions on the covariance matrix, we derive accurate bounds both in expectation and probability. Our bounds have clear interpretations that enable us to derive properties and motivate practical choices for the covariance matrix resulting in efficient low-rank approximation algorithms. The most commonly used bounds in the literature have been demonstrated as a specific instance of the bounds proposed here, with the additional contribution of being tighter. Numerical experiments related to data assimilation further illustrate that exploiting the problem structure to select the covariance matrix improves the performance as suggested by our bounds.

High-dimensional mixed-categorical Gaussian processes with application to multidisciplinary design optimization for a green aircraft

Multidisciplinary design optimization (MDO) methods aim at adapting numerical optimization techniques to the design of engineering systems involving multiple disciplines. In this context, a large number of mixed continuous, integer, and categorical variables might arise during the optimization process, and practical applications involve a significant number of design variables. Recently, there has been a growing interest in mixed-categorical metamodels based on Gaussian Process (GP) for Bayesian optimization. In particular, to handle mixed-categorical variables, several existing approaches employ different strategies to build the GP. These strategies either use continuous kernels, such as the continuous relaxation or the Gower distance-based kernels, or direct estimation of the correlation matrix, such as the exponential homoscedastic hypersphere (EHH) or the Homoscedastic Hypersphere (HH) kernel. Although the EHH and HH kernels are shown to be very efficient and lead to accurate GPs, they are based on a large number of hyperparameters. In this paper, we address this issue by constructing mixed-categorical GPs with fewer hyperparameters using Partial Least Squares (PLS) regression. Our goal is to generalize Kriging with PLS, commonly used for continuous inputs, to handle mixed-categorical inputs. The proposed method is implemented in the open-source software SMT and has been efficiently applied to structural and multidisciplinary applications. Our method is used to effectively demonstrate the structural behavior of a cantilever beam and facilitates MDO of a green aircraft, resulting in a 439-kilogram reduction in the amount of fuel consumed during a single aircraft mission.

SMT 2.0: A Surrogate Modeling Toolbox with a focus on Hierarchical and Mixed Variables Gaussian Processes

The Surrogate Modeling Toolbox (SMT) is an open-source Python package that offers a collection of surrogate modeling methods, sampling techniques, and a set of sample problems. This paper presents SMT 2.0, a major new release of SMT that introduces significant upgrades and new features to the toolbox. This release adds the capability to handle mixed-variable surrogate models and hierarchical variables. These types of variables are becoming increasingly important in several surrogate modeling applications. SMT 2.0 also improves SMT by extending sampling methods, adding new surrogate models, and computing variance and kernel derivatives for Kriging. This release also includes new functions to handle noisy and use multifidelity data. To the best of our knowledge, SMT 2.0 is the first open-source surrogate library to propose surrogate models for hierarchical and mixed inputs. This open-source software is distributed under the New BSD license.

A Globally Convergent Evolutionary Strategy for Stochastic Constrained Optimization with Applications to Reinforcement Learning

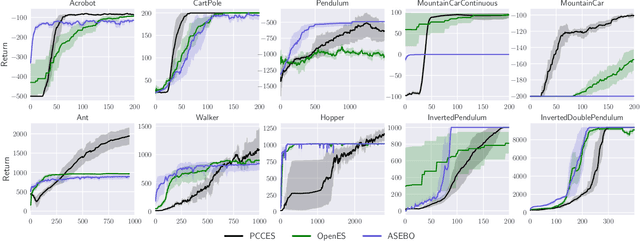
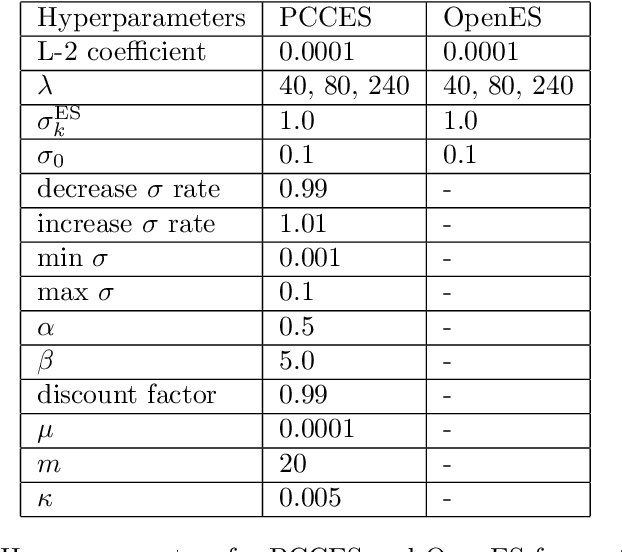
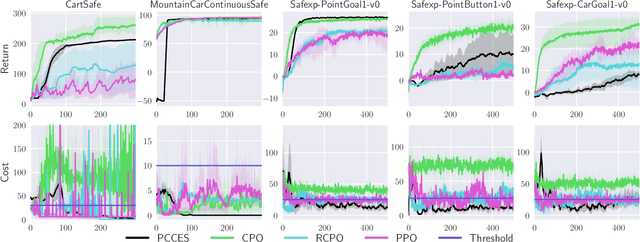
Evolutionary strategies have recently been shown to achieve competing levels of performance for complex optimization problems in reinforcement learning. In such problems, one often needs to optimize an objective function subject to a set of constraints, including for instance constraints on the entropy of a policy or to restrict the possible set of actions or states accessible to an agent. Convergence guarantees for evolutionary strategies to optimize stochastic constrained problems are however lacking in the literature. In this work, we address this problem by designing a novel optimization algorithm with a sufficient decrease mechanism that ensures convergence and that is based only on estimates of the functions. We demonstrate the applicability of this algorithm on two types of experiments: i) a control task for maximizing rewards and ii) maximizing rewards subject to a non-relaxable set of constraints.

Direct-Search for a Class of Stochastic Min-Max Problems

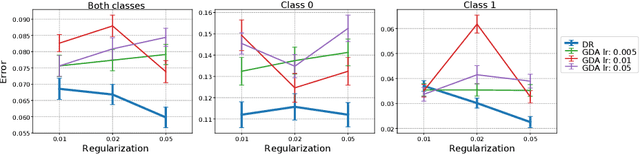
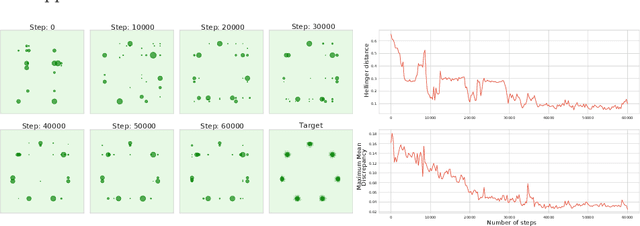
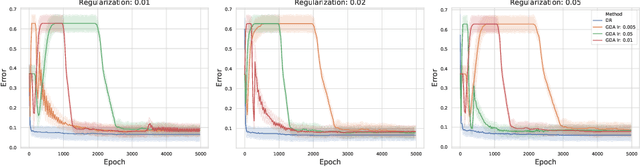
Recent applications in machine learning have renewed the interest of the community in min-max optimization problems. While gradient-based optimization methods are widely used to solve such problems, there are however many scenarios where these techniques are not well-suited, or even not applicable when the gradient is not accessible. We investigate the use of direct-search methods that belong to a class of derivative-free techniques that only access the objective function through an oracle. In this work, we design a novel algorithm in the context of min-max saddle point games where one sequentially updates the min and the max player. We prove convergence of this algorithm under mild assumptions, where the objective of the max-player satisfies the Polyak-\L{}ojasiewicz (PL) condition, while the min-player is characterized by a nonconvex objective. Our method only assumes dynamically adjusted accurate estimates of the oracle with a fixed probability. To the best of our knowledge, our analysis is the first one to address the convergence of a direct-search method for min-max objectives in a stochastic setting.