A general error analysis for randomized low-rank approximation with application to data assimilation

Randomized algorithms have proven to perform well on a large class of numerical linear algebra problems. Their theoretical analysis is critical to provide guarantees on their behaviour, and in this sense, the stochastic analysis of the randomized low-rank approximation error plays a central role. Indeed, several randomized methods for the approximation of dominant eigen- or singular modes can be rewritten as low-rank approximation methods. However, despite the large variety of algorithms, the existing theoretical frameworks for their analysis rely on a specific structure for the covariance matrix that is not adapted to all the algorithms. We propose a general framework for the stochastic analysis of the low-rank approximation error in Frobenius norm for centered and non-standard Gaussian matrices. Under minimal assumptions on the covariance matrix, we derive accurate bounds both in expectation and probability. Our bounds have clear interpretations that enable us to derive properties and motivate practical choices for the covariance matrix resulting in efficient low-rank approximation algorithms. The most commonly used bounds in the literature have been demonstrated as a specific instance of the bounds proposed here, with the additional contribution of being tighter. Numerical experiments related to data assimilation further illustrate that exploiting the problem structure to select the covariance matrix improves the performance as suggested by our bounds.

Latent Space Data Assimilation by using Deep Learning

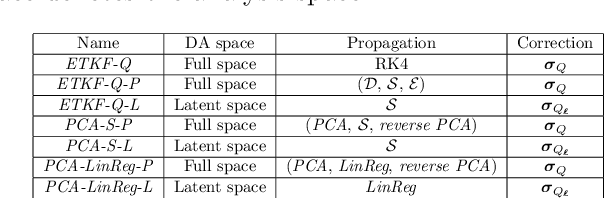
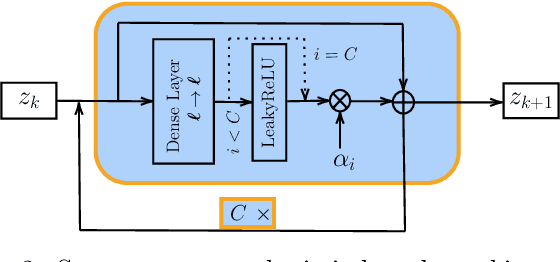
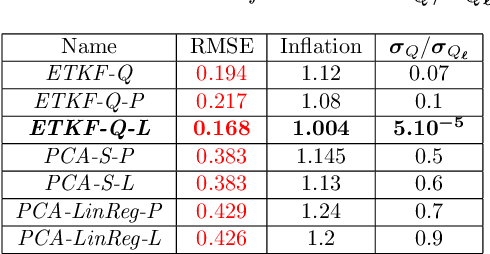
Performing Data Assimilation (DA) at a low cost is of prime concern in Earth system modeling, particularly at the time of big data where huge quantities of observations are available. Capitalizing on the ability of Neural Networks techniques for approximating the solution of PDE's, we incorporate Deep Learning (DL) methods into a DA framework. More precisely, we exploit the latent structure provided by autoencoders (AEs) to design an Ensemble Transform Kalman Filter with model error (ETKF-Q) in the latent space. Model dynamics are also propagated within the latent space via a surrogate neural network. This novel ETKF-Q-Latent (thereafter referred to as ETKF-Q-L) algorithm is tested on a tailored instructional version of Lorenz 96 equations, named the augmented Lorenz 96 system: it possesses a latent structure that accurately represents the observed dynamics. Numerical experiments based on this particular system evidence that the ETKF-Q-L approach both reduces the computational cost and provides better accuracy than state of the art algorithms, such as the ETKF-Q.

DAN -- An optimal Data Assimilation framework based on machine learning Recurrent Networks

Data assimilation algorithms aim at forecasting the state of a dynamical system by combining a mathematical representation of the system with noisy observations thereof. We propose a fully data driven deep learning architecture generalizing recurrent Elman networks and data assimilation algorithms which provably reaches the same prediction goals as the latter. On numerical experiments based on the well-known Lorenz system and when suitably trained using snapshots of the system trajectory (i.e. batches of state trajectories) and observations, our architecture successfully reconstructs both the analysis and the propagation of probability density functions of the system state at a given time conditioned to past observations.