A general error analysis for randomized low-rank approximation with application to data assimilation

Randomized algorithms have proven to perform well on a large class of numerical linear algebra problems. Their theoretical analysis is critical to provide guarantees on their behaviour, and in this sense, the stochastic analysis of the randomized low-rank approximation error plays a central role. Indeed, several randomized methods for the approximation of dominant eigen- or singular modes can be rewritten as low-rank approximation methods. However, despite the large variety of algorithms, the existing theoretical frameworks for their analysis rely on a specific structure for the covariance matrix that is not adapted to all the algorithms. We propose a general framework for the stochastic analysis of the low-rank approximation error in Frobenius norm for centered and non-standard Gaussian matrices. Under minimal assumptions on the covariance matrix, we derive accurate bounds both in expectation and probability. Our bounds have clear interpretations that enable us to derive properties and motivate practical choices for the covariance matrix resulting in efficient low-rank approximation algorithms. The most commonly used bounds in the literature have been demonstrated as a specific instance of the bounds proposed here, with the additional contribution of being tighter. Numerical experiments related to data assimilation further illustrate that exploiting the problem structure to select the covariance matrix improves the performance as suggested by our bounds.

TREGO: a Trust-Region Framework for Efficient Global Optimization

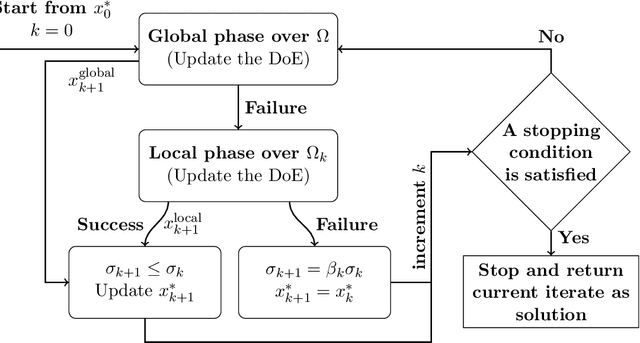
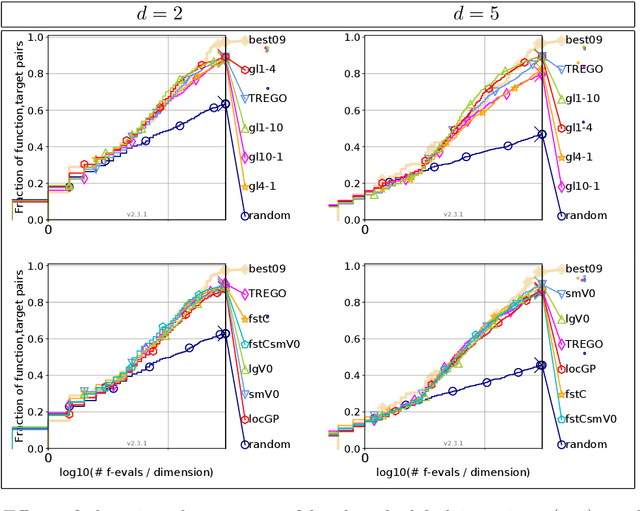
Efficient Global Optimization (EGO) is the canonical form of Bayesian optimization that has been successfully applied to solve global optimization of expensive-to-evaluate black-box problems. However, EGO struggles to scale with dimension, and offers limited theoretical guarantees. In this work, we propose and analyze a trust-region-like EGO method (TREGO). TREGO alternates between regular EGO steps and local steps within a trust region. By following a classical scheme for the trust region (based on a sufficient decrease condition), we demonstrate that our algorithm enjoys strong global convergence properties, while departing from EGO only for a subset of optimization steps. Using extensive numerical experiments based on the well-known COCO benchmark, we first analyze the sensitivity of TREGO to its own parameters, then show that the resulting algorithm is consistently outperforming EGO and getting competitive with other state-of-the-art global optimization methods. The method is available both in the R package DiceOptim (https://cran.r-project.org/package=DiceOptim) and Python library trieste (https://secondmind-labs.github.io/trieste/).