FunQuant: A R package to perform quantization in the context of rare events and time-consuming simulations

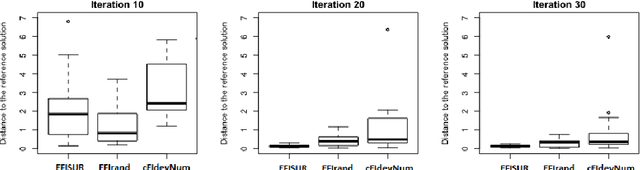
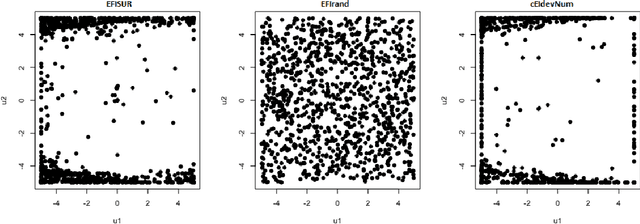
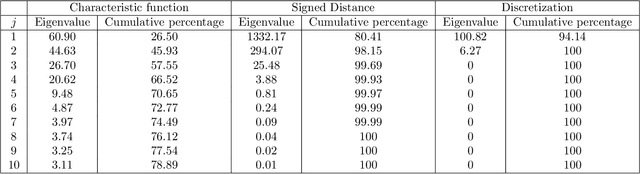
Quantization summarizes continuous distributions by calculating a discrete approximation. Among the widely adopted methods for data quantization is Lloyd's algorithm, which partitions the space into Vorono\"i cells, that can be seen as clusters, and constructs a discrete distribution based on their centroids and probabilistic masses. Lloyd's algorithm estimates the optimal centroids in a minimal expected distance sense, but this approach poses significant challenges in scenarios where data evaluation is costly, and relates to rare events. Then, the single cluster associated to no event takes the majority of the probability mass. In this context, a metamodel is required and adapted sampling methods are necessary to increase the precision of the computations on the rare clusters.

A comparison of mixed-variables Bayesian optimization approaches

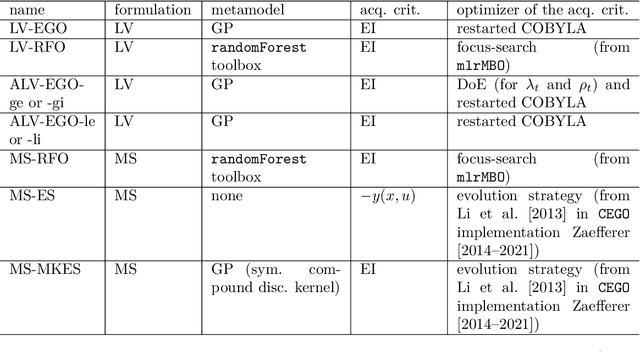
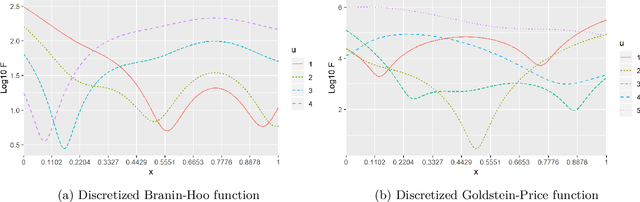
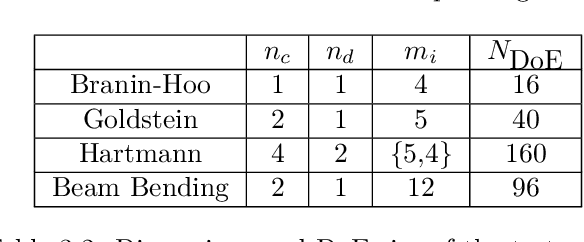
Most real optimization problems are defined over a mixed search space where the variables are both discrete and continuous. In engineering applications, the objective function is typically calculated with a numerically costly black-box simulation.General mixed and costly optimization problems are therefore of a great practical interest, yet their resolution remains in a large part an open scientific question. In this article, costly mixed problems are approached through Gaussian processes where the discrete variables are relaxed into continuous latent variables. The continuous space is more easily harvested by classical Bayesian optimization techniques than a mixed space would. Discrete variables are recovered either subsequently to the continuous optimization, or simultaneously with an additional continuous-discrete compatibility constraint that is handled with augmented Lagrangians. Several possible implementations of such Bayesian mixed optimizers are compared. In particular, the reformulation of the problem with continuous latent variables is put in competition with searches working directly in the mixed space. Among the algorithms involving latent variables and an augmented Lagrangian, a particular attention is devoted to the Lagrange multipliers for which a local and a global estimation techniques are studied. The comparisons are based on the repeated optimization of three analytical functions and a beam design problem.

Revisiting Bayesian Optimization in the light of the COCO benchmark

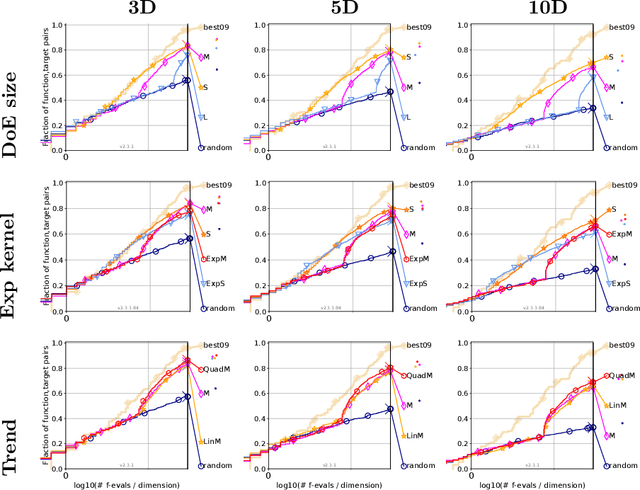
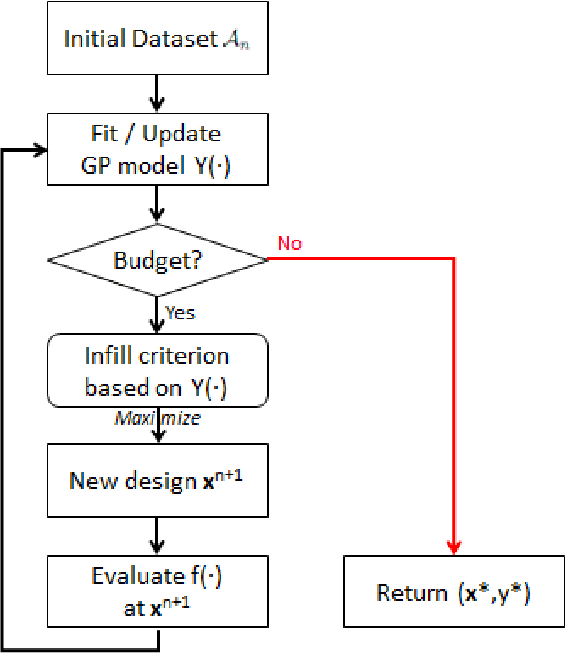
It is commonly believed that Bayesian optimization (BO) algorithms are highly efficient for optimizing numerically costly functions. However, BO is not often compared to widely different alternatives, and is mostly tested on narrow sets of problems (multimodal, low-dimensional functions), which makes it difficult to assess where (or if) they actually achieve state-of-the-art performance. Moreover, several aspects in the design of these algorithms vary across implementations without a clear recommendation emerging from current practices, and many of these design choices are not substantiated by authoritative test campaigns. This article reports a large investigation about the effects on the performance of (Gaussian process based) BO of common and less common design choices. The experiments are carried out with the established COCO (COmparing Continuous Optimizers) software. It is found that a small initial budget, a quadratic trend, high-quality optimization of the acquisition criterion bring consistent progress. Using the GP mean as an occasional acquisition contributes to a negligible additional improvement. Warping degrades performance. The Mat\'ern 5/2 kernel is a good default but it may be surpassed by the exponential kernel on irregular functions. Overall, the best EGO variants are competitive or improve over state-of-the-art algorithms in dimensions less or equal to 5 for multimodal functions. The code developed for this study makes the new version (v2.1.1) of the R package DiceOptim available on CRAN. The structure of the experiments by function groups allows to define priorities for future research on Bayesian optimization.

A sampling criterion for constrained Bayesian optimization with uncertainties

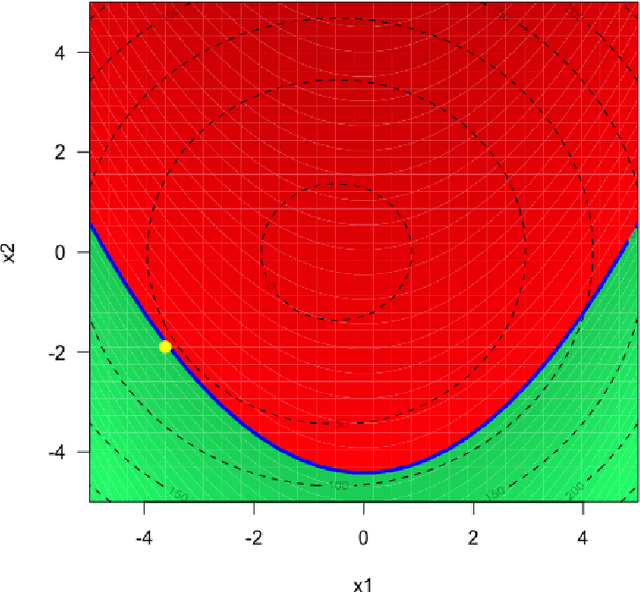
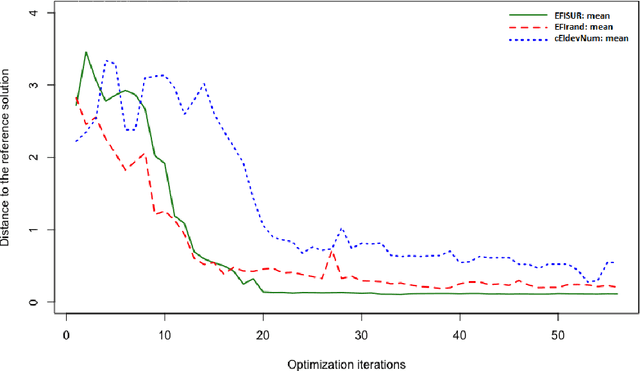
We consider the problem of chance constrained optimization where it is sought to optimize a function and satisfy constraints, both of which are affected by uncertainties. The real world declinations of this problem are particularly challenging because of their inherent computational cost. To tackle such problems, we propose a new Bayesian optimization method. It applies to the situation where the uncertainty comes from some of the inputs, so that it becomes possible to define an acquisition criterion in the joint controlled-uncontrolled input space. The main contribution of this work is an acquisition criterion that accounts for both the average improvement in objective function and the constraint reliability. The criterion is derived following the Stepwise Uncertainty Reduction logic and its maximization provides both optimal controlled and uncontrolled parameters. Analytical expressions are given to efficiently calculate the criterion. Numerical studies on test functions are presented. It is found through experimental comparisons with alternative sampling criteria that the adequation between the sampling criterion and the problem contributes to the efficiency of the overall optimization. As a side result, an expression for the variance of the improvement is given.

TREGO: a Trust-Region Framework for Efficient Global Optimization

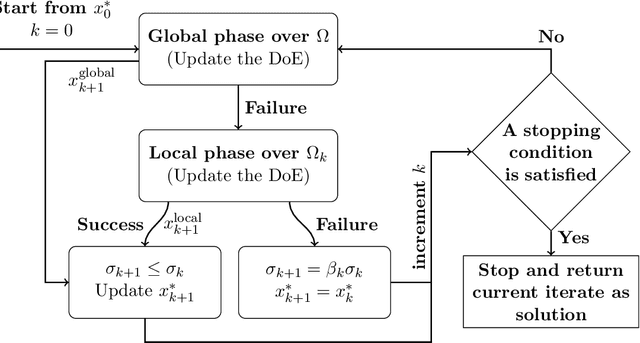
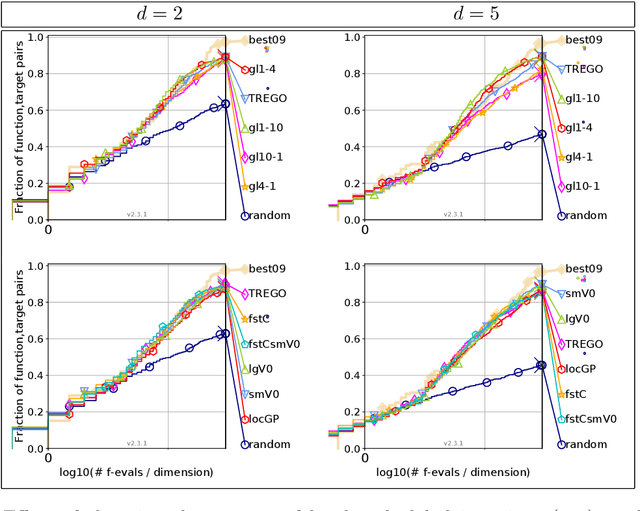
Efficient Global Optimization (EGO) is the canonical form of Bayesian optimization that has been successfully applied to solve global optimization of expensive-to-evaluate black-box problems. However, EGO struggles to scale with dimension, and offers limited theoretical guarantees. In this work, we propose and analyze a trust-region-like EGO method (TREGO). TREGO alternates between regular EGO steps and local steps within a trust region. By following a classical scheme for the trust region (based on a sufficient decrease condition), we demonstrate that our algorithm enjoys strong global convergence properties, while departing from EGO only for a subset of optimization steps. Using extensive numerical experiments based on the well-known COCO benchmark, we first analyze the sensitivity of TREGO to its own parameters, then show that the resulting algorithm is consistently outperforming EGO and getting competitive with other state-of-the-art global optimization methods. The method is available both in the R package DiceOptim (https://cran.r-project.org/package=DiceOptim) and Python library trieste (https://secondmind-labs.github.io/trieste/).

Modeling and Optimization with Gaussian Processes in Reduced Eigenbases -- Extended Version

Parametric shape optimization aims at minimizing an objective function f(x) where x are CAD parameters. This task is difficult when f is the output of an expensive-to-evaluate numerical simulator and the number of CAD parameters is large. Most often, the set of all considered CAD shapes resides in a manifold of lower effective dimension in which it is preferable to build the surrogate model and perform the optimization. In this work, we uncover the manifold through a high-dimensional shape mapping and build a new coordinate system made of eigenshapes. The surrogate model is learned in the space of eigenshapes: a regularized likelihood maximization provides the most relevant dimensions for the output. The final surrogate model is detailed (anisotropic) with respect to the most sensitive eigenshapes and rough (isotropic) in the remaining dimensions. Last, the optimization is carried out with a focus on the critical dimensions, the remaining ones being coarsely optimized through a random embedding and the manifold being accounted for through a replication strategy. At low budgets, the methodology leads to a more accurate model and a faster optimization than the classical approach of directly working with the CAD parameters.

Global sensitivity analysis for optimization with variable selection

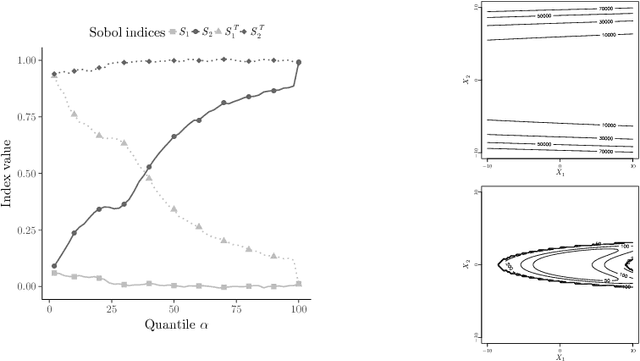
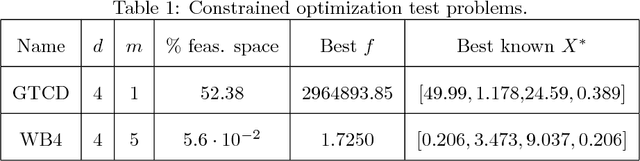
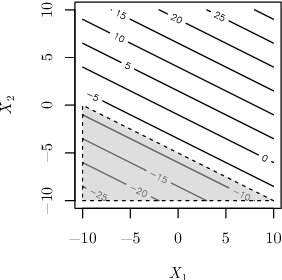
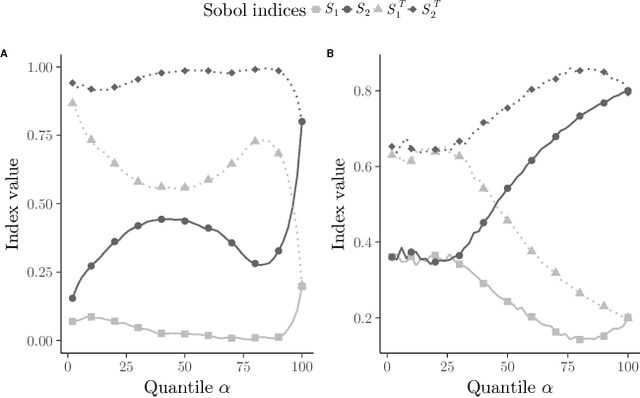
The optimization of high dimensional functions is a key issue in engineering problems but it frequently comes at a cost that is not acceptable since it usually involves a complex and expensive computer code. Engineers often overcome this limitation by first identifying which parameters drive the most the function variations: non-influential variables are set to a fixed value and the optimization procedure is carried out with the remaining influential variables. Such variable selection is performed through influence measures that are meaningful for regression problems. However it does not account for the specific structure of optimization problems where we would like to identify which variables most lead to constraints satisfaction and low values of the objective function. In this paper, we propose a new sensitivity analysis that accounts for the specific aspects of optimization problems. In particular, we introduce an influence measure based on the Hilbert-Schmidt Independence Criterion to characterize whether a design variable matters to reach low values of the objective function and to satisfy the constraints. This sensitivity measure makes it possible to sort the inputs and reduce the problem dimension. We compare a random and a greedy strategies to set the values of the non-influential variables before conducting a local optimization. Applications to several test-cases show that this variable selection and the greedy strategy significantly reduce the number of function evaluations at a limited cost in terms of solution performance.

Targeting Solutions in Bayesian Multi-Objective Optimization: Sequential and Parallel Versions

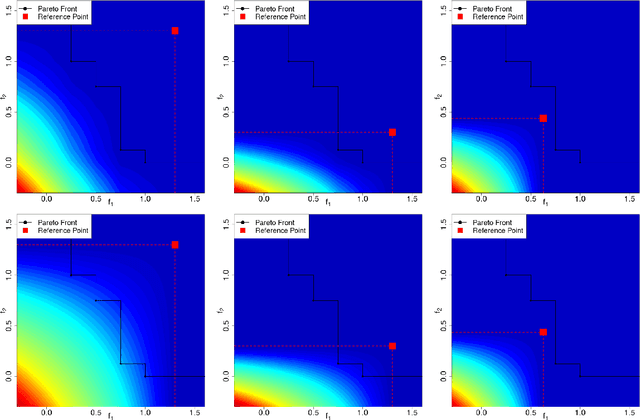
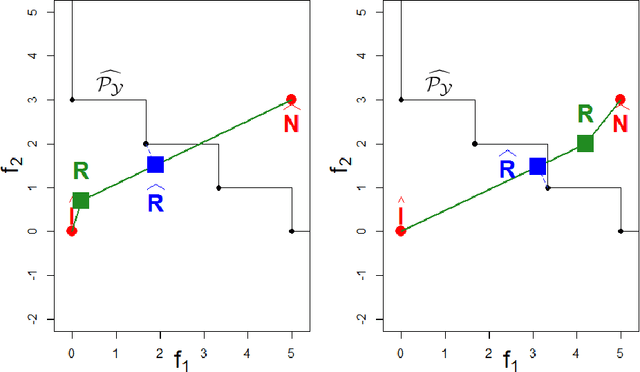
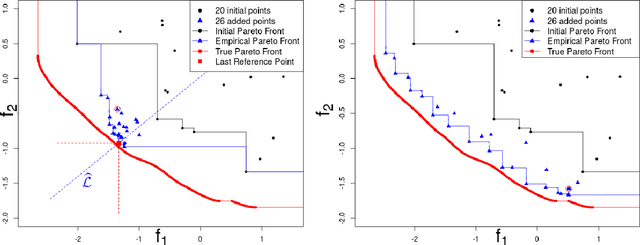
Multi-objective optimization aims at finding trade-off solutions to conflicting objectives. These constitute the Pareto optimal set. In the context of expensive-to-evaluate functions, it is impossible and often non-informative to look for the entire set. As an end-user would typically prefer a certain part of the objective space, we modify the Bayesian multi-objective optimization algorithm which uses Gaussian Processes to maximize the Expected Hypervolume Improvement, to focus the search in the preferred region. The cumulated effects of the Gaussian Processes and the targeting strategy lead to a particularly efficient convergence to the desired part of the Pareto set. To take advantage of parallel computing, a multi-point extension of the targeting criterion is proposed and analyzed.

Budgeted Multi-Objective Optimization with a Focus on the Central Part of the Pareto Front - Extended Version

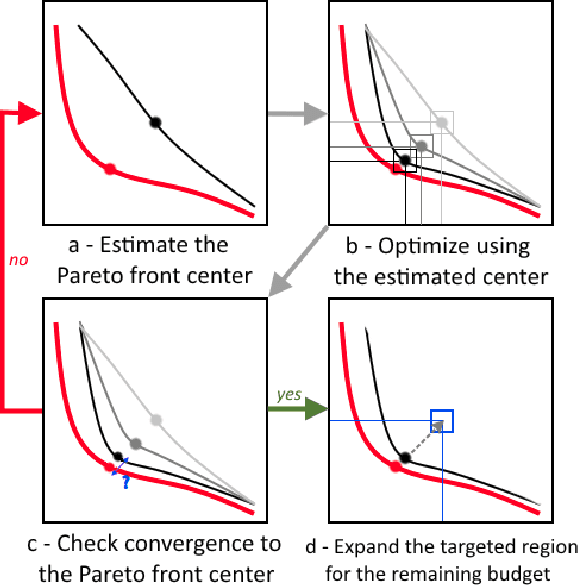
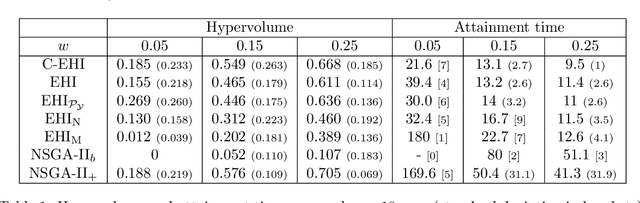
Optimizing nonlinear systems involving expensive (computer) experiments with regard to conflicting objectives is a common challenge. When the number of experiments is severely restricted and/or when the number of objectives increases, uncovering the whole set of optimal solutions (the Pareto front) is out of reach, even for surrogate-based approaches. As non-compromising Pareto optimal solutions have usually little point in applications, this work restricts the search to relevant solutions that are close to the Pareto front center. The article starts by characterizing this center. Next, a Bayesian multi-objective optimization method for directing the search towards it is proposed. A criterion for detecting convergence to the center is described. If the criterion is triggered, a widened central part of the Pareto front is targeted such that sufficiently accurate convergence to it is forecasted within the remaining budget. Numerical experiments show how the resulting algorithm, C-EHI, better locates the central part of the Pareto front when compared to state-of-the-art Bayesian algorithms.

An analytic comparison of regularization methods for Gaussian Processes

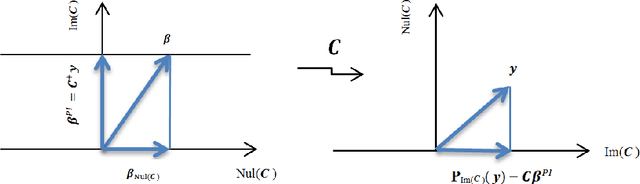
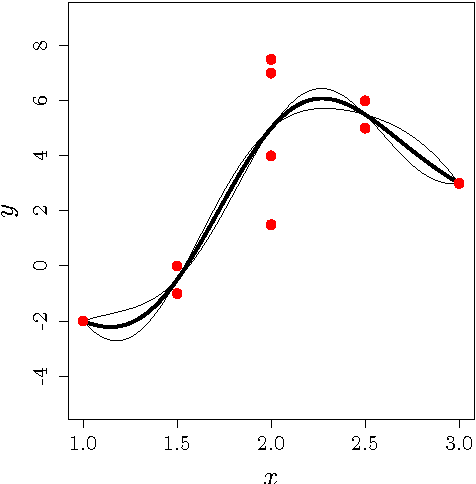
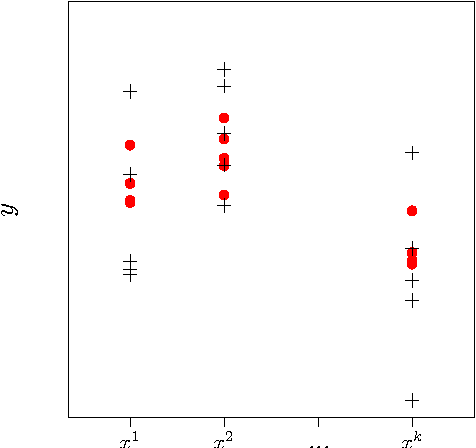
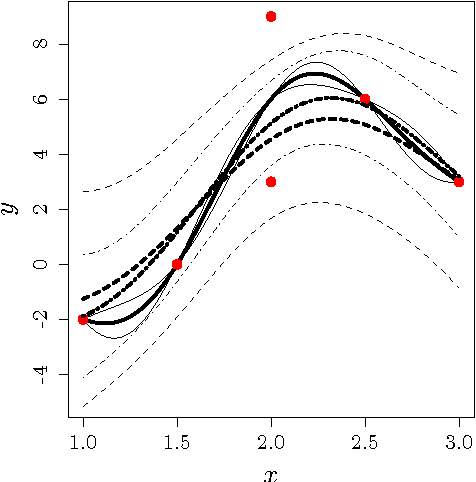
Gaussian Processes (GPs) are a popular approach to predict the output of a parameterized experiment. They have many applications in the field of Computer Experiments, in particular to perform sensitivity analysis, adaptive design of experiments and global optimization. Nearly all of the applications of GPs require the inversion of a covariance matrix that, in practice, is often ill-conditioned. Regularization methodologies are then employed with consequences on the GPs that need to be better understood.The two principal methods to deal with ill-conditioned covariance matrices are i) pseudoinverse and ii) adding a positive constant to the diagonal (the so-called nugget regularization).The first part of this paper provides an algebraic comparison of PI and nugget regularizations. Redundant points, responsible for covariance matrix singularity, are defined. It is proven that pseudoinverse regularization, contrarily to nugget regularization, averages the output values and makes the variance zero at redundant points. However, pseudoinverse and nugget regularizations become equivalent as the nugget value vanishes. A measure for data-model discrepancy is proposed which serves for choosing a regularization technique.In the second part of the paper, a distribution-wise GP is introduced that interpolates Gaussian distributions instead of data points. Distribution-wise GP can be seen as an improved regularization method for GPs.