Budgeted Multi-Objective Optimization with a Focus on the Central Part of the Pareto Front - Extended Version

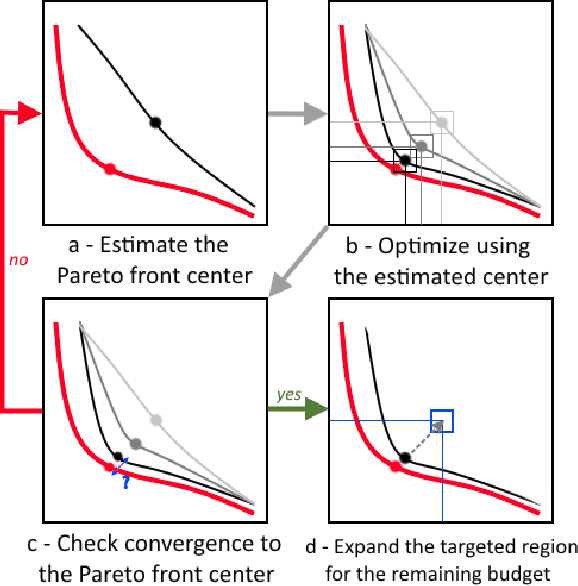
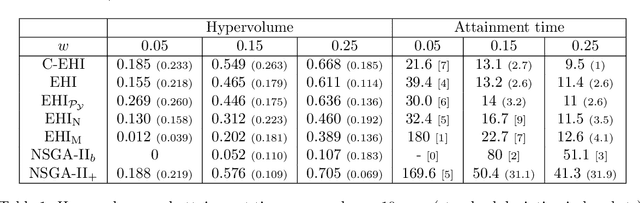
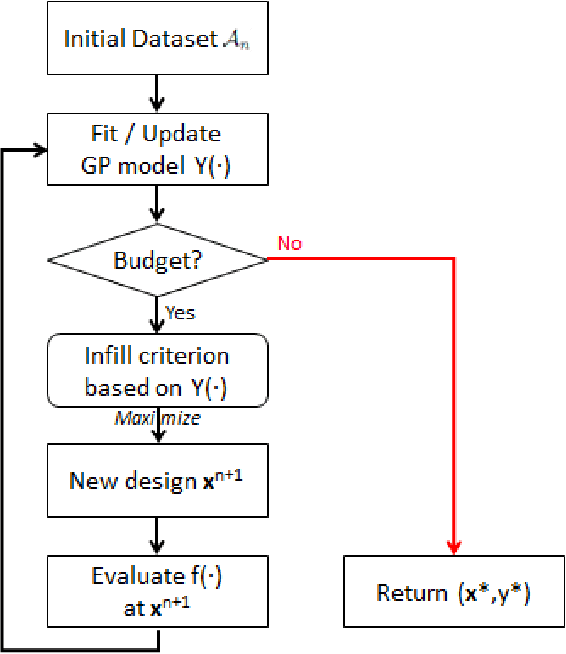
Optimizing nonlinear systems involving expensive (computer) experiments with regard to conflicting objectives is a common challenge. When the number of experiments is severely restricted and/or when the number of objectives increases, uncovering the whole set of optimal solutions (the Pareto front) is out of reach, even for surrogate-based approaches. As non-compromising Pareto optimal solutions have usually little point in applications, this work restricts the search to relevant solutions that are close to the Pareto front center. The article starts by characterizing this center. Next, a Bayesian multi-objective optimization method for directing the search towards it is proposed. A criterion for detecting convergence to the center is described. If the criterion is triggered, a widened central part of the Pareto front is targeted such that sufficiently accurate convergence to it is forecasted within the remaining budget. Numerical experiments show how the resulting algorithm, C-EHI, better locates the central part of the Pareto front when compared to state-of-the-art Bayesian algorithms.