Combining additivity and active subspaces for high-dimensional Gaussian process modeling

Gaussian processes are a widely embraced technique for regression and classification due to their good prediction accuracy, analytical tractability and built-in capabilities for uncertainty quantification. However, they suffer from the curse of dimensionality whenever the number of variables increases. This challenge is generally addressed by assuming additional structure in theproblem, the preferred options being either additivity or low intrinsic dimensionality. Our contribution for high-dimensional Gaussian process modeling is to combine them with a multi-fidelity strategy, showcasing the advantages through experiments on synthetic functions and datasets.

Spherical Inducing Features for Orthogonally-Decoupled Gaussian Processes

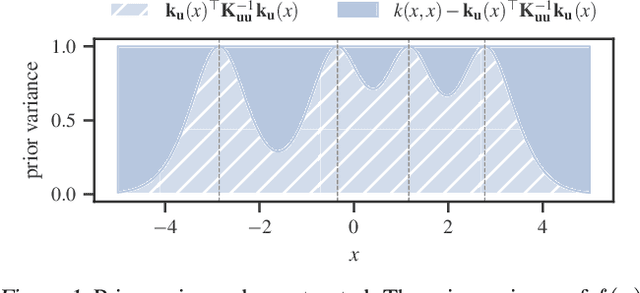
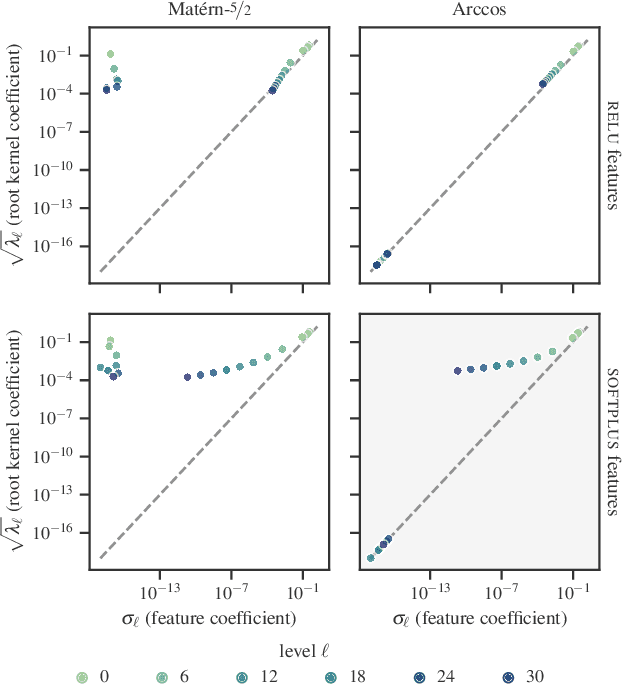
Despite their many desirable properties, Gaussian processes (GPs) are often compared unfavorably to deep neural networks (NNs) for lacking the ability to learn representations. Recent efforts to bridge the gap between GPs and deep NNs have yielded a new class of inter-domain variational GPs in which the inducing variables correspond to hidden units of a feedforward NN. In this work, we examine some practical issues associated with this approach and propose an extension that leverages the orthogonal decomposition of GPs to mitigate these limitations. In particular, we introduce spherical inter-domain features to construct more flexible data-dependent basis functions for both the principal and orthogonal components of the GP approximation and show that incorporating NN activation features under this framework not only alleviates these shortcomings but is more scalable than alternative strategies. Experiments on multiple benchmark datasets demonstrate the effectiveness of our approach.

Trieste: Efficiently Exploring The Depths of Black-box Functions with TensorFlow

We present Trieste, an open-source Python package for Bayesian optimization and active learning benefiting from the scalability and efficiency of TensorFlow. Our library enables the plug-and-play of popular TensorFlow-based models within sequential decision-making loops, e.g. Gaussian processes from GPflow or GPflux, or neural networks from Keras. This modular mindset is central to the package and extends to our acquisition functions and the internal dynamics of the decision-making loop, both of which can be tailored and extended by researchers or engineers when tackling custom use cases. Trieste is a research-friendly and production-ready toolkit backed by a comprehensive test suite, extensive documentation, and available at https://github.com/secondmind-labs/trieste.

Inducing Point Allocation for Sparse Gaussian Processes in High-Throughput Bayesian Optimisation

Sparse Gaussian Processes are a key component of high-throughput Bayesian Optimisation (BO) loops; however, we show that existing methods for allocating their inducing points severely hamper optimisation performance. By exploiting the quality-diversity decomposition of Determinantal Point Processes, we propose the first inducing point allocation strategy designed specifically for use in BO. Unlike existing methods which seek only to reduce global uncertainty in the objective function, our approach provides the local high-fidelity modelling of promising regions required for precise optimisation. More generally, we demonstrate that our proposed framework provides a flexible way to allocate modelling capacity in sparse models and so is suitable broad range of downstream sequential decision making tasks.

Fantasizing with Dual GPs in Bayesian Optimization and Active Learning

Gaussian processes (GPs) are the main surrogate functions used for sequential modelling such as Bayesian Optimization and Active Learning. Their drawbacks are poor scaling with data and the need to run an optimization loop when using a non-Gaussian likelihood. In this paper, we focus on `fantasizing' batch acquisition functions that need the ability to condition on new fantasized data computationally efficiently. By using a sparse Dual GP parameterization, we gain linear scaling with batch size as well as one-step updates for non-Gaussian likelihoods, thus extending sparse models to greedy batch fantasizing acquisition functions.

A penalisation method for batch multi-objective Bayesian optimisation with application in heat exchanger design

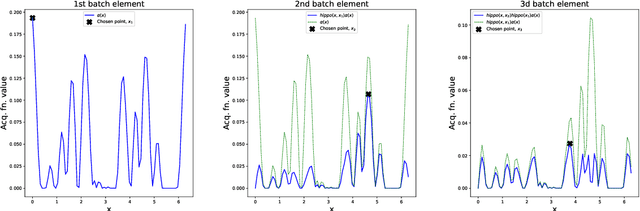
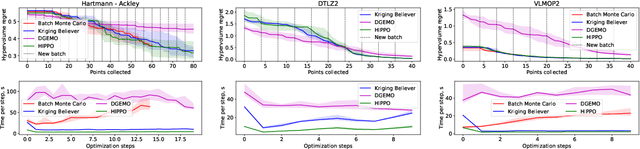
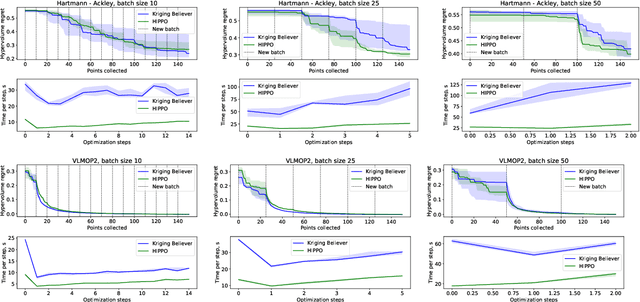
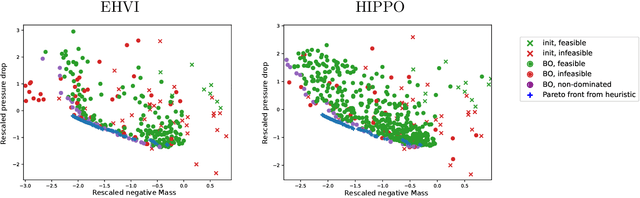
We present HIghly Parallelisable Pareto Optimisation (HIPPO) -- a batch acquisition function that enables multi-objective Bayesian optimisation methods to efficiently exploit parallel processing resources. Multi-Objective Bayesian Optimisation (MOBO) is a very efficient tool for tackling expensive black-box problems. However, most MOBO algorithms are designed as purely sequential strategies, and existing batch approaches are prohibitively expensive for all but the smallest of batch sizes. We show that by encouraging batch diversity through penalising evaluations with similar predicted objective values, HIPPO is able to cheaply build large batches of informative points. Our extensive experimental validation demonstrates that HIPPO is at least as efficient as existing alternatives whilst incurring an order of magnitude lower computational overhead and scaling easily to batch sizes considerably higher than currently supported in the literature. Additionally, we demonstrate the application of HIPPO to a challenging heat exchanger design problem, stressing the real-world utility of our highly parallelisable approach to MOBO.

Information-theoretic Inducing Point Placement for High-throughput Bayesian Optimisation

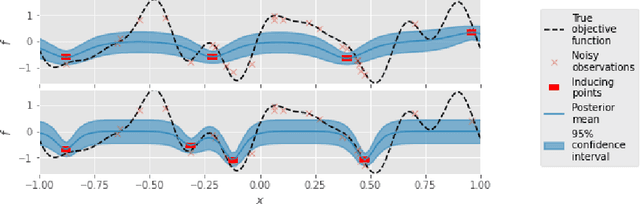
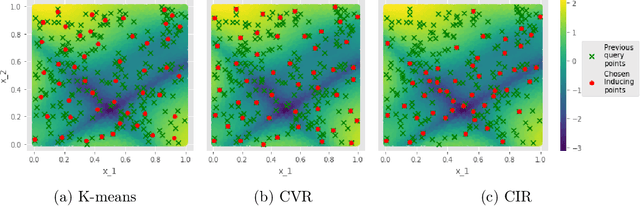
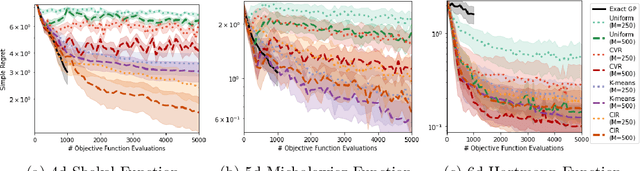
Sparse Gaussian Processes are a key component of high-throughput Bayesian optimisation (BO) loops -- an increasingly common setting where evaluation budgets are large and highly parallelised. By using representative subsets of the available data to build approximate posteriors, sparse models dramatically reduce the computational costs of surrogate modelling by relying on a small set of pseudo-observations, the so-called inducing points, in lieu of the full data set. However, current approaches to design inducing points are not appropriate within BO loops as they seek to reduce global uncertainty in the objective function. Thus, the high-fidelity modelling of promising and data-dense regions required for precise optimisation is sacrificed and computational resources are instead wasted on modelling areas of the space already known to be sub-optimal. Inspired by entropy-based BO methods, we propose a novel inducing point design that uses a principled information-theoretic criterion to select inducing points. By choosing inducing points to maximally reduce both global uncertainty and uncertainty in the maximum value of the objective function, we build surrogate models able to support high-precision high-throughput BO.

Revisiting Bayesian Optimization in the light of the COCO benchmark

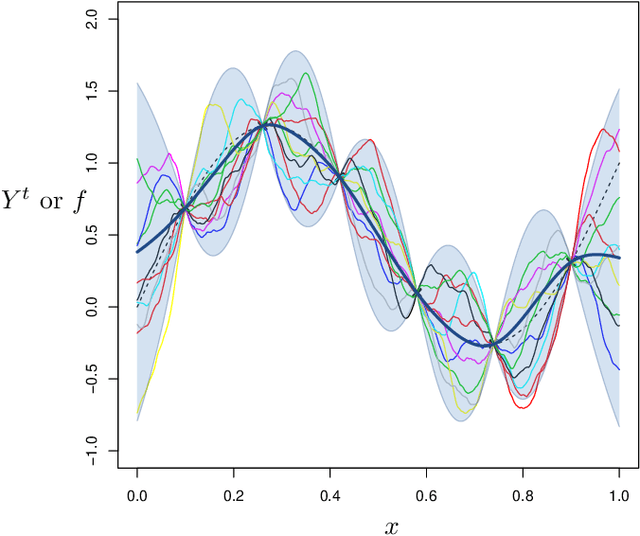
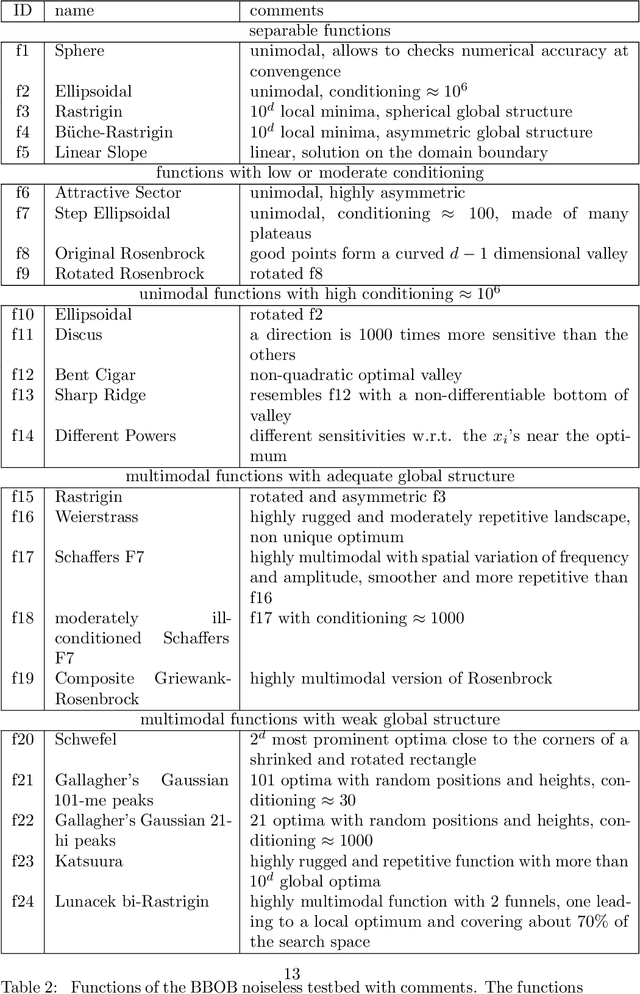
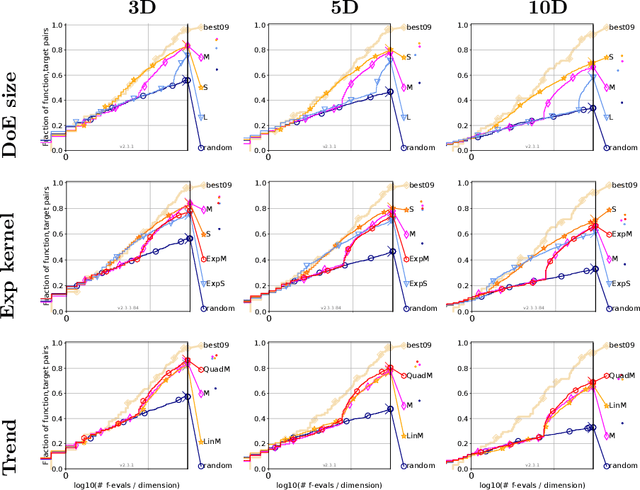
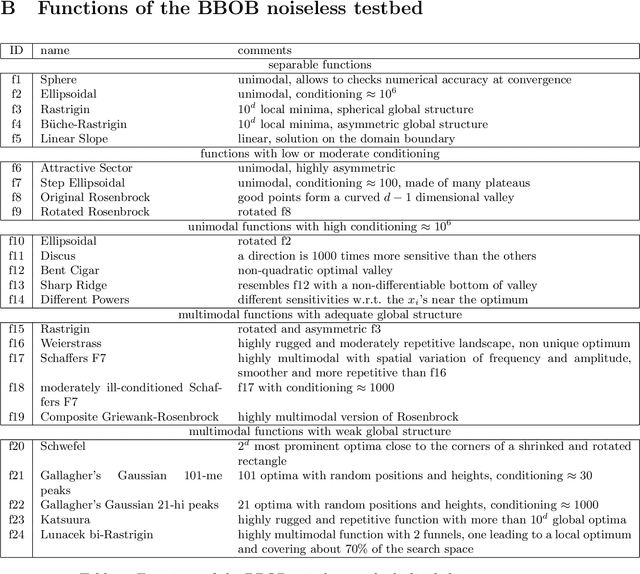
It is commonly believed that Bayesian optimization (BO) algorithms are highly efficient for optimizing numerically costly functions. However, BO is not often compared to widely different alternatives, and is mostly tested on narrow sets of problems (multimodal, low-dimensional functions), which makes it difficult to assess where (or if) they actually achieve state-of-the-art performance. Moreover, several aspects in the design of these algorithms vary across implementations without a clear recommendation emerging from current practices, and many of these design choices are not substantiated by authoritative test campaigns. This article reports a large investigation about the effects on the performance of (Gaussian process based) BO of common and less common design choices. The experiments are carried out with the established COCO (COmparing Continuous Optimizers) software. It is found that a small initial budget, a quadratic trend, high-quality optimization of the acquisition criterion bring consistent progress. Using the GP mean as an occasional acquisition contributes to a negligible additional improvement. Warping degrades performance. The Mat\'ern 5/2 kernel is a good default but it may be surpassed by the exponential kernel on irregular functions. Overall, the best EGO variants are competitive or improve over state-of-the-art algorithms in dimensions less or equal to 5 for multimodal functions. The code developed for this study makes the new version (v2.1.1) of the R package DiceOptim available on CRAN. The structure of the experiments by function groups allows to define priorities for future research on Bayesian optimization.

TREGO: a Trust-Region Framework for Efficient Global Optimization

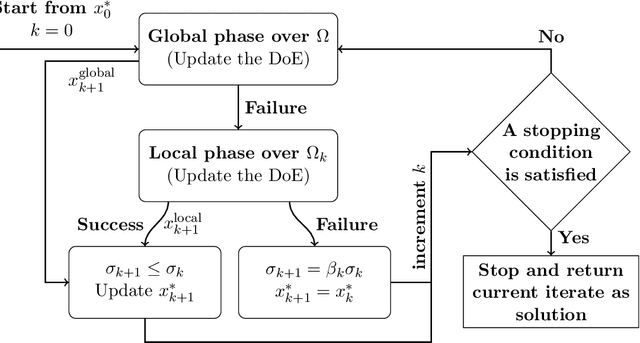
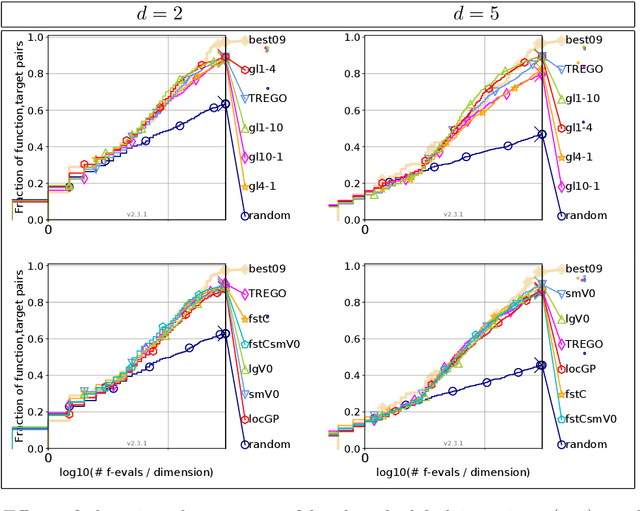
Efficient Global Optimization (EGO) is the canonical form of Bayesian optimization that has been successfully applied to solve global optimization of expensive-to-evaluate black-box problems. However, EGO struggles to scale with dimension, and offers limited theoretical guarantees. In this work, we propose and analyze a trust-region-like EGO method (TREGO). TREGO alternates between regular EGO steps and local steps within a trust region. By following a classical scheme for the trust region (based on a sufficient decrease condition), we demonstrate that our algorithm enjoys strong global convergence properties, while departing from EGO only for a subset of optimization steps. Using extensive numerical experiments based on the well-known COCO benchmark, we first analyze the sensitivity of TREGO to its own parameters, then show that the resulting algorithm is consistently outperforming EGO and getting competitive with other state-of-the-art global optimization methods. The method is available both in the R package DiceOptim (https://cran.r-project.org/package=DiceOptim) and Python library trieste (https://secondmind-labs.github.io/trieste/).