Plan$\times$RAG: Planning-guided Retrieval Augmented Generation

We introduce Planning-guided Retrieval Augmented Generation (Plan$\times$RAG), a novel framework that augments the \emph{retrieve-then-reason} paradigm of existing RAG frameworks to \emph{plan-then-retrieve}. Plan$\times$RAG formulates a reasoning plan as a directed acyclic graph (DAG), decomposing queries into interrelated atomic sub-queries. Answer generation follows the DAG structure, allowing significant gains in efficiency through parallelized retrieval and generation. While state-of-the-art RAG solutions require extensive data generation and fine-tuning of language models (LMs), Plan$\times$RAG incorporates frozen LMs as plug-and-play experts to generate high-quality answers. Compared to existing RAG solutions, Plan$\times$RAG demonstrates significant improvements in reducing hallucinations and bolstering attribution due to its structured sub-query decomposition. Overall, Plan$\times$RAG offers a new perspective on integrating external knowledge in LMs while ensuring attribution by design, contributing towards more reliable LM-based systems.

Memory-Based Dual Gaussian Processes for Sequential Learning

Sequential learning with Gaussian processes (GPs) is challenging when access to past data is limited, for example, in continual and active learning. In such cases, errors can accumulate over time due to inaccuracies in the posterior, hyperparameters, and inducing points, making accurate learning challenging. Here, we present a method to keep all such errors in check using the recently proposed dual sparse variational GP. Our method enables accurate inference for generic likelihoods and improves learning by actively building and updating a memory of past data. We demonstrate its effectiveness in several applications involving Bayesian optimization, active learning, and continual learning.

Variational Gaussian Process Diffusion Processes

Diffusion processes are a class of stochastic differential equations (SDEs) providing a rich family of expressive models that arise naturally in dynamic modelling tasks. Probabilistic inference and learning under generative models with latent processes endowed with a non-linear diffusion process prior are intractable problems. We build upon work within variational inference approximating the posterior process as a linear diffusion process, point out pathologies in the approach, and propose an alternative parameterization of the Gaussian variational process using a continuous exponential family description. This allows us to trade a slow inference algorithm with fixed-point iterations for a fast algorithm for convex optimization akin to natural gradient descent, which also provides a better objective for the learning of model parameters.

Fantasizing with Dual GPs in Bayesian Optimization and Active Learning

Gaussian processes (GPs) are the main surrogate functions used for sequential modelling such as Bayesian Optimization and Active Learning. Their drawbacks are poor scaling with data and the need to run an optimization loop when using a non-Gaussian likelihood. In this paper, we focus on `fantasizing' batch acquisition functions that need the ability to condition on new fantasized data computationally efficiently. By using a sparse Dual GP parameterization, we gain linear scaling with batch size as well as one-step updates for non-Gaussian likelihoods, thus extending sparse models to greedy batch fantasizing acquisition functions.

Scalable Inference in SDEs by Direct Matching of the Fokker-Planck-Kolmogorov Equation

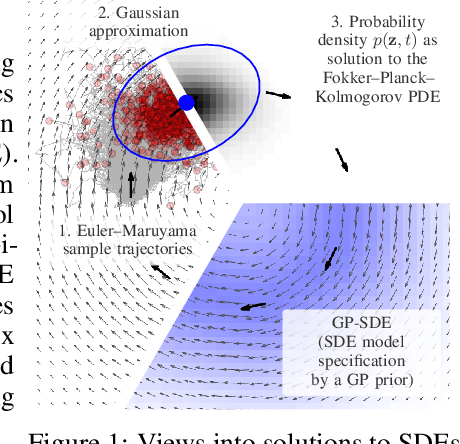
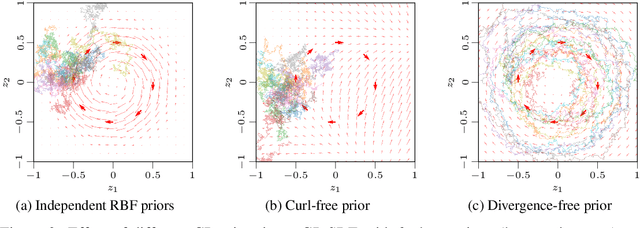
Simulation-based techniques such as variants of stochastic Runge-Kutta are the de facto approach for inference with stochastic differential equations (SDEs) in machine learning. These methods are general-purpose and used with parametric and non-parametric models, and neural SDEs. Stochastic Runge-Kutta relies on the use of sampling schemes that can be inefficient in high dimensions. We address this issue by revisiting the classical SDE literature and derive direct approximations to the (typically intractable) Fokker-Planck-Kolmogorov equation by matching moments. We show how this workflow is fast, scales to high-dimensional latent spaces, and is applicable to scarce-data applications, where a non-parametric SDE with a driving Gaussian process velocity field specifies the model.