Variational Gaussian Process Diffusion Processes

Diffusion processes are a class of stochastic differential equations (SDEs) providing a rich family of expressive models that arise naturally in dynamic modelling tasks. Probabilistic inference and learning under generative models with latent processes endowed with a non-linear diffusion process prior are intractable problems. We build upon work within variational inference approximating the posterior process as a linear diffusion process, point out pathologies in the approach, and propose an alternative parameterization of the Gaussian variational process using a continuous exponential family description. This allows us to trade a slow inference algorithm with fixed-point iterations for a fast algorithm for convex optimization akin to natural gradient descent, which also provides a better objective for the learning of model parameters.

Dual Parameterization of Sparse Variational Gaussian Processes

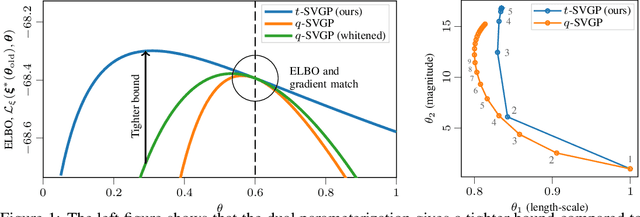
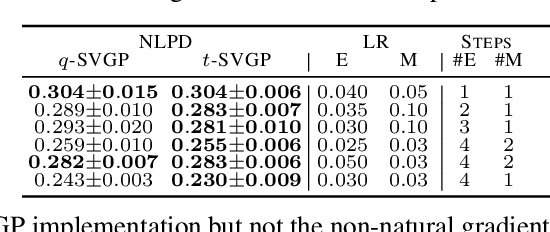
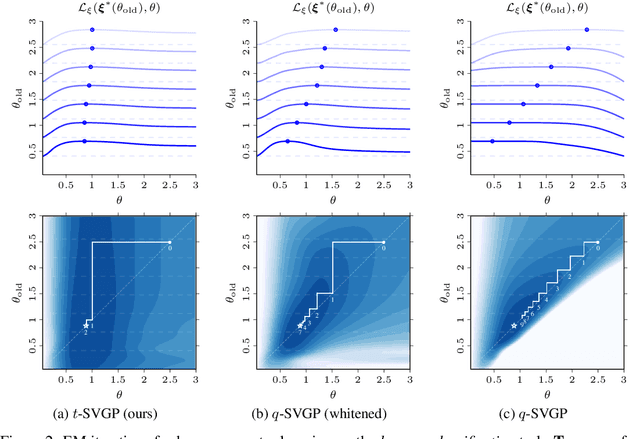
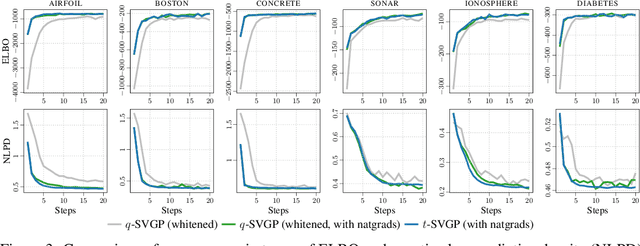
Sparse variational Gaussian process (SVGP) methods are a common choice for non-conjugate Gaussian process inference because of their computational benefits. In this paper, we improve their computational efficiency by using a dual parameterization where each data example is assigned dual parameters, similarly to site parameters used in expectation propagation. Our dual parameterization speeds-up inference using natural gradient descent, and provides a tighter evidence lower bound for hyperparameter learning. The approach has the same memory cost as the current SVGP methods, but it is faster and more accurate.

Bellman: A Toolbox for Model-Based Reinforcement Learning in TensorFlow

In the past decade, model-free reinforcement learning (RL) has provided solutions to challenging domains such as robotics. Model-based RL shows the prospect of being more sample-efficient than model-free methods in terms of agent-environment interactions, because the model enables to extrapolate to unseen situations. In the more recent past, model-based methods have shown superior results compared to model-free methods in some challenging domains with non-linear state transitions. At the same time, it has become apparent that RL is not market-ready yet and that many real-world applications are going to require model-based approaches, because model-free methods are too sample-inefficient and show poor performance in early stages of training. The latter is particularly important in industry, e.g. in production systems that directly impact a company's revenue. This demonstrates the necessity for a toolbox to push the boundaries for model-based RL. While there is a plethora of toolboxes for model-free RL, model-based RL has received little attention in terms of toolbox development. Bellman aims to fill this gap and introduces the first thoroughly designed and tested model-based RL toolbox using state-of-the-art software engineering practices. Our modular approach enables to combine a wide range of environment models with generic model-based agent classes that recover state-of-the-art algorithms. We also provide an experiment harness to compare both model-free and model-based agents in a systematic fashion w.r.t. user-defined evaluation metrics (e.g. cumulative reward). This paves the way for new research directions, e.g. investigating uncertainty-aware environment models that are not necessarily neural-network-based, or developing algorithms to solve industrially-motivated benchmarks that share characteristics with real-world problems.

Sparse Algorithms for Markovian Gaussian Processes

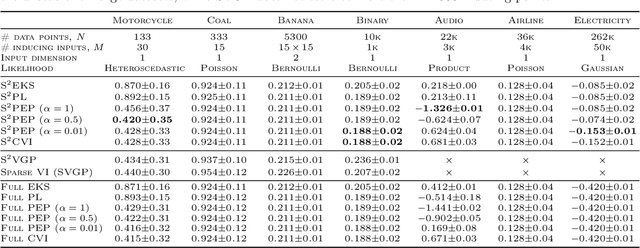
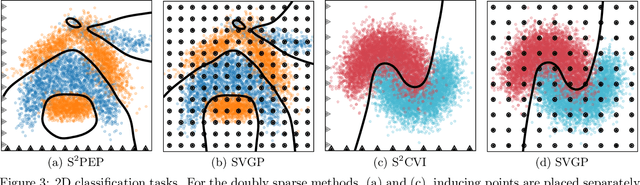
Approximate Bayesian inference methods that scale to very large datasets are crucial in leveraging probabilistic models for real-world time series. Sparse Markovian Gaussian processes combine the use of inducing variables with efficient Kalman filter-like recursions, resulting in algorithms whose computational and memory requirements scale linearly in the number of inducing points, whilst also enabling parallel parameter updates and stochastic optimisation. Under this paradigm, we derive a general site-based approach to approximate inference, whereby we approximate the non-Gaussian likelihood with local Gaussian terms, called sites. Our approach results in a suite of novel sparse extensions to algorithms from both the machine learning and signal processing literature, including variational inference, expectation propagation, and the classical nonlinear Kalman smoothers. The derived methods are suited to large time series, and we also demonstrate their applicability to spatio-temporal data, where the model has separate inducing points in both time and space.

A Framework for Interdomain and Multioutput Gaussian Processes

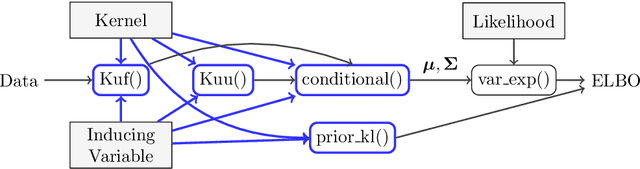
One obstacle to the use of Gaussian processes (GPs) in large-scale problems, and as a component in deep learning system, is the need for bespoke derivations and implementations for small variations in the model or inference. In order to improve the utility of GPs we need a modular system that allows rapid implementation and testing, as seen in the neural network community. We present a mathematical and software framework for scalable approximate inference in GPs, which combines interdomain approximations and multiple outputs. Our framework, implemented in GPflow, provides a unified interface for many existing multioutput models, as well as more recent convolutional structures. This simplifies the creation of deep models with GPs, and we hope that this work will encourage more interest in this approach.

Doubly Sparse Variational Gaussian Processes

The use of Gaussian process models is typically limited to datasets with a few tens of thousands of observations due to their complexity and memory footprint. The two most commonly used methods to overcome this limitation are 1) the variational sparse approximation which relies on inducing points and 2) the state-space equivalent formulation of Gaussian processes which can be seen as exploiting some sparsity in the precision matrix. We propose to take the best of both worlds: we show that the inducing point framework is still valid for state space models and that it can bring further computational and memory savings. Furthermore, we provide the natural gradient formulation for the proposed variational parameterisation. Finally, this work makes it possible to use the state-space formulation inside deep Gaussian process models as illustrated in one of the experiments.

Disentangled Skill Embeddings for Reinforcement Learning

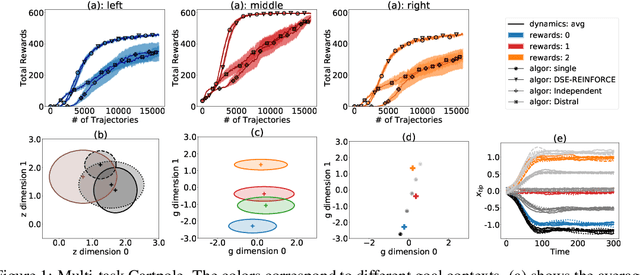
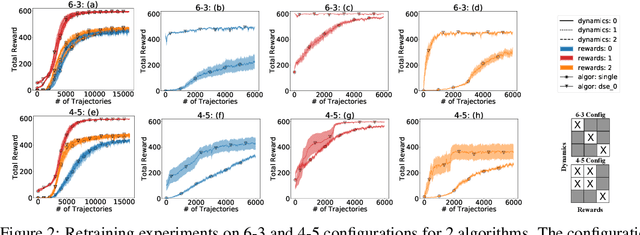
We propose a novel framework for multi-task reinforcement learning (MTRL). Using a variational inference formulation, we learn policies that generalize across both changing dynamics and goals. The resulting policies are parametrized by shared parameters that allow for transfer between different dynamics and goal conditions, and by task-specific latent-space embeddings that allow for specialization to particular tasks. We show how the latent-spaces enable generalization to unseen dynamics and goals conditions. Additionally, policies equipped with such embeddings serve as a space of skills (or options) for hierarchical reinforcement learning. Since we can change task dynamics and goals independently, we name our framework Disentangled Skill Embeddings (DSE).

Banded Matrix Operators for Gaussian Markov Models in the Automatic Differentiation Era

Banded matrices can be used as precision matrices in several models including linear state-space models, some Gaussian processes, and Gaussian Markov random fields. The aim of the paper is to make modern inference methods (such as variational inference or gradient-based sampling) available for Gaussian models with banded precision. We show that this can efficiently be achieved by equipping an automatic differentiation framework, such as TensorFlow or PyTorch, with some linear algebra operators dedicated to banded matrices. This paper studies the algorithmic aspects of the required operators, details their reverse-mode derivatives, and show that their complexity is linear in the number of observations.

Scalable GAM using sparse variational Gaussian processes

Generalized additive models (GAMs) are a widely used class of models of interest to statisticians as they provide a flexible way to design interpretable models of data beyond linear models. We here propose a scalable and well-calibrated Bayesian treatment of GAMs using Gaussian processes (GPs) and leveraging recent advances in variational inference. We use sparse GPs to represent each component and exploit the additive structure of the model to efficiently represent a Gaussian a posteriori coupling between the components.

Discrete flow posteriors for variational inference in discrete dynamical systems

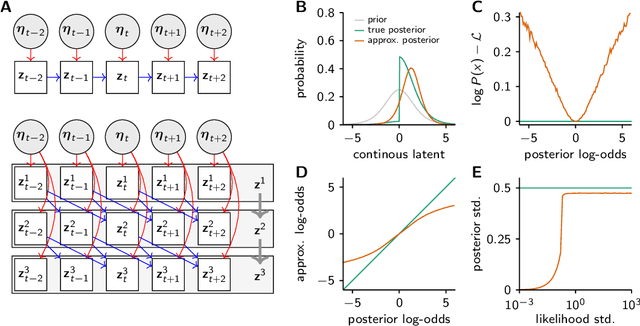
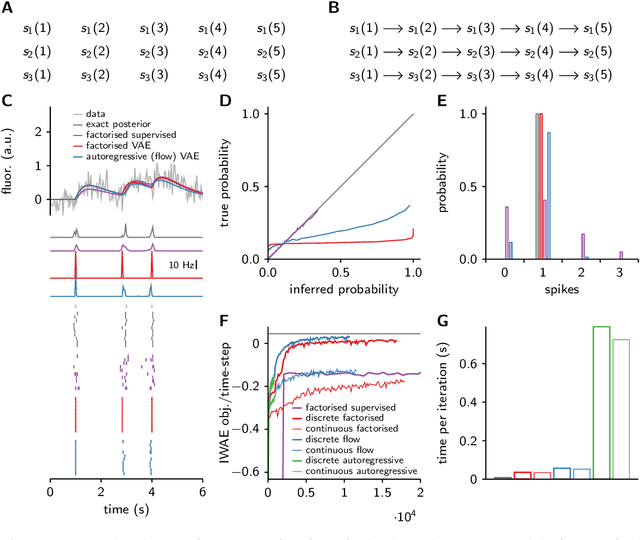
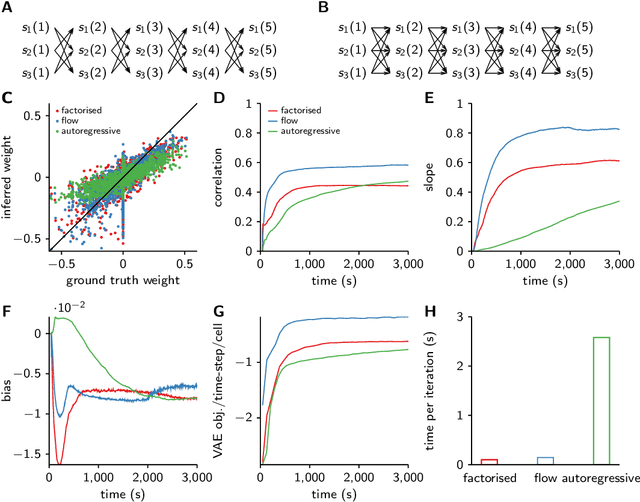
Each training step for a variational autoencoder (VAE) requires us to sample from the approximate posterior, so we usually choose simple (e.g. factorised) approximate posteriors in which sampling is an efficient computation that fully exploits GPU parallelism. However, such simple approximate posteriors are often insufficient, as they eliminate statistical dependencies in the posterior. While it is possible to use normalizing flow approximate posteriors for continuous latents, some problems have discrete latents and strong statistical dependencies. The most natural approach to model these dependencies is an autoregressive distribution, but sampling from such distributions is inherently sequential and thus slow. We develop a fast, parallel sampling procedure for autoregressive distributions based on fixed-point iterations which enables efficient and accurate variational inference in discrete state-space latent variable dynamical systems. To optimize the variational bound, we considered two ways to evaluate probabilities: inserting the relaxed samples directly into the pmf for the discrete distribution, or converting to continuous logistic latent variables and interpreting the K-step fixed-point iterations as a normalizing flow. We found that converting to continuous latent variables gave considerable additional scope for mismatch between the true and approximate posteriors, which resulted in biased inferences, we thus used the former approach. Using our fast sampling procedure, we were able to realize the benefits of correlated posteriors, including accurate uncertainty estimates for one cell, and accurate connectivity estimates for multiple cells, in an order of magnitude less time.