Sparse Gaussian Processes with Spherical Harmonic Features Revisited

We revisit the Gaussian process model with spherical harmonic features and study connections between the associated RKHS, its eigenstructure and deep models. Based on this, we introduce a new class of kernels which correspond to deep models of continuous depth. In our formulation, depth can be estimated as a kernel hyper-parameter by optimizing the evidence lower bound. Further, we introduce sparseness in the eigenbasis by variational learning of the spherical harmonic phases. This enables scaling to larger input dimensions than previously, while also allowing for learning of high frequency variations. We validate our approach on machine learning benchmark datasets.

Doubly Sparse Variational Gaussian Processes

The use of Gaussian process models is typically limited to datasets with a few tens of thousands of observations due to their complexity and memory footprint. The two most commonly used methods to overcome this limitation are 1) the variational sparse approximation which relies on inducing points and 2) the state-space equivalent formulation of Gaussian processes which can be seen as exploiting some sparsity in the precision matrix. We propose to take the best of both worlds: we show that the inducing point framework is still valid for state space models and that it can bring further computational and memory savings. Furthermore, we provide the natural gradient formulation for the proposed variational parameterisation. Finally, this work makes it possible to use the state-space formulation inside deep Gaussian process models as illustrated in one of the experiments.

Banded Matrix Operators for Gaussian Markov Models in the Automatic Differentiation Era

Banded matrices can be used as precision matrices in several models including linear state-space models, some Gaussian processes, and Gaussian Markov random fields. The aim of the paper is to make modern inference methods (such as variational inference or gradient-based sampling) available for Gaussian models with banded precision. We show that this can efficiently be achieved by equipping an automatic differentiation framework, such as TensorFlow or PyTorch, with some linear algebra operators dedicated to banded matrices. This paper studies the algorithmic aspects of the required operators, details their reverse-mode derivatives, and show that their complexity is linear in the number of observations.

Natural Gradients in Practice: Non-Conjugate Variational Inference in Gaussian Process Models

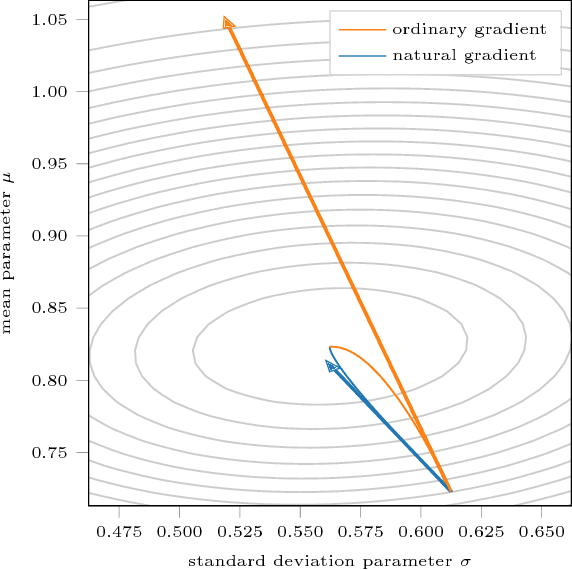
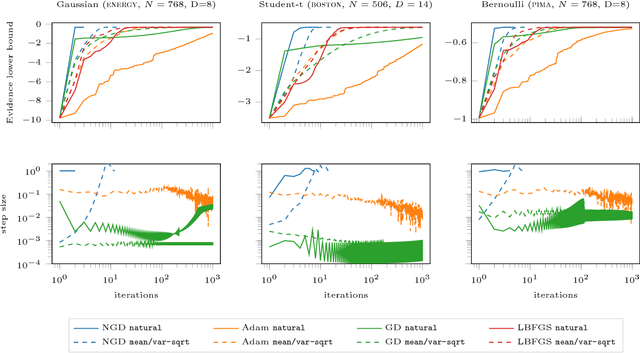
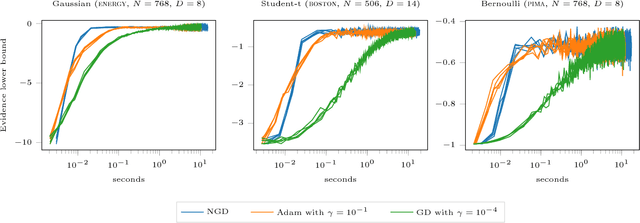
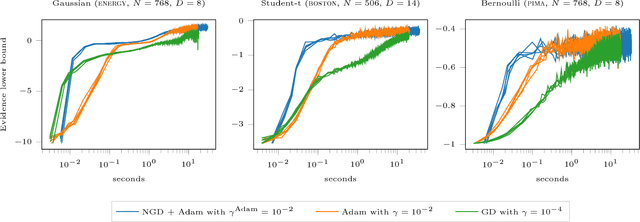
The natural gradient method has been used effectively in conjugate Gaussian process models, but the non-conjugate case has been largely unexplored. We examine how natural gradients can be used in non-conjugate stochastic settings, together with hyperparameter learning. We conclude that the natural gradient can significantly improve performance in terms of wall-clock time. For ill-conditioned posteriors the benefit of the natural gradient method is especially pronounced, and we demonstrate a practical setting where ordinary gradients are unusable. We show how natural gradients can be computed efficiently and automatically in any parameterization, using automatic differentiation. Our code is integrated into the GPflow package.

Identification of Gaussian Process State Space Models

The Gaussian process state space model (GPSSM) is a non-linear dynamical system, where unknown transition and/or measurement mappings are described by GPs. Most research in GPSSMs has focussed on the state estimation problem, i.e., computing a posterior of the latent state given the model. However, the key challenge in GPSSMs has not been satisfactorily addressed yet: system identification, i.e., learning the model. To address this challenge, we impose a structured Gaussian variational posterior distribution over the latent states, which is parameterised by a recognition model in the form of a bi-directional recurrent neural network. Inference with this structure allows us to recover a posterior smoothed over sequences of data. We provide a practical algorithm for efficiently computing a lower bound on the marginal likelihood using the reparameterisation trick. This further allows for the use of arbitrary kernels within the GPSSM. We demonstrate that the learnt GPSSM can efficiently generate plausible future trajectories of the identified system after only observing a small number of episodes from the true system.

DeepCoder: Semi-parametric Variational Autoencoders for Automatic Facial Action Coding

Human face exhibits an inherent hierarchy in its representations (i.e., holistic facial expressions can be encoded via a set of facial action units (AUs) and their intensity). Variational (deep) auto-encoders (VAE) have shown great results in unsupervised extraction of hierarchical latent representations from large amounts of image data, while being robust to noise and other undesired artifacts. Potentially, this makes VAEs a suitable approach for learning facial features for AU intensity estimation. Yet, most existing VAE-based methods apply classifiers learned separately from the encoded features. By contrast, the non-parametric (probabilistic) approaches, such as Gaussian Processes (GPs), typically outperform their parametric counterparts, but cannot deal easily with large amounts of data. To this end, we propose a novel VAE semi-parametric modeling framework, named DeepCoder, which combines the modeling power of parametric (convolutional) and nonparametric (ordinal GPs) VAEs, for joint learning of (1) latent representations at multiple levels in a task hierarchy1, and (2) classification of multiple ordinal outputs. We show on benchmark datasets for AU intensity estimation that the proposed DeepCoder outperforms the state-of-the-art approaches, and related VAEs and deep learning models.

Variational Gaussian Process Auto-Encoder for Ordinal Prediction of Facial Action Units

We address the task of simultaneous feature fusion and modeling of discrete ordinal outputs. We propose a novel Gaussian process(GP) auto-encoder modeling approach. In particular, we introduce GP encoders to project multiple observed features onto a latent space, while GP decoders are responsible for reconstructing the original features. Inference is performed in a novel variational framework, where the recovered latent representations are further constrained by the ordinal output labels. In this way, we seamlessly integrate the ordinal structure in the learned manifold, while attaining robust fusion of the input features. We demonstrate the representation abilities of our model on benchmark datasets from machine learning and affect analysis. We further evaluate the model on the tasks of feature fusion and joint ordinal prediction of facial action units. Our experiments demonstrate the benefits of the proposed approach compared to the state of the art.

Gaussian Process Domain Experts for Model Adaptation in Facial Behavior Analysis

We present a novel approach for supervised domain adaptation that is based upon the probabilistic framework of Gaussian processes (GPs). Specifically, we introduce domain-specific GPs as local experts for facial expression classification from face images. The adaptation of the classifier is facilitated in probabilistic fashion by conditioning the target expert on multiple source experts. Furthermore, in contrast to existing adaptation approaches, we also learn a target expert from available target data solely. Then, a single and confident classifier is obtained by combining the predictions from multiple experts based on their confidence. Learning of the model is efficient and requires no retraining/reweighting of the source classifiers. We evaluate the proposed approach on two publicly available datasets for multi-class (MultiPIE) and multi-label (DISFA) facial expression classification. To this end, we perform adaptation of two contextual factors: 'where' (view) and 'who' (subject). We show in our experiments that the proposed approach consistently outperforms both source and target classifiers, while using as few as 30 target examples. It also outperforms the state-of-the-art approaches for supervised domain adaptation.