Natural Gradients in Practice: Non-Conjugate Variational Inference in Gaussian Process Models
Paper and Code
Mar 24, 2018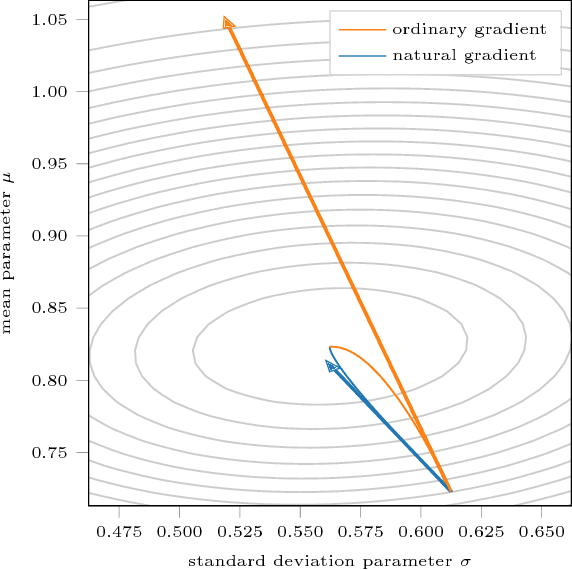
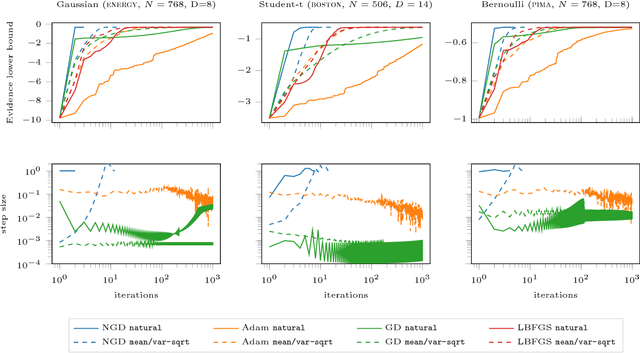
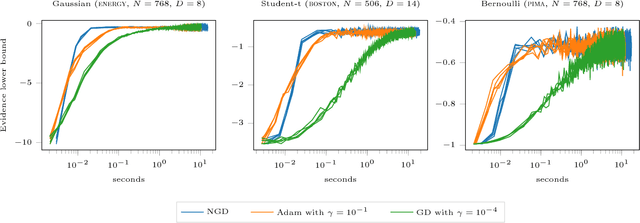
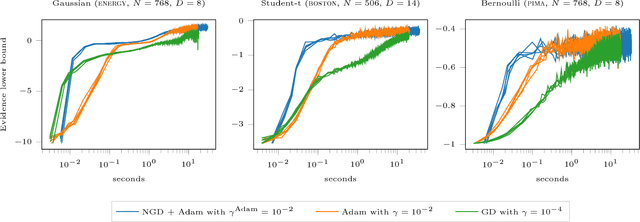
The natural gradient method has been used effectively in conjugate Gaussian process models, but the non-conjugate case has been largely unexplored. We examine how natural gradients can be used in non-conjugate stochastic settings, together with hyperparameter learning. We conclude that the natural gradient can significantly improve performance in terms of wall-clock time. For ill-conditioned posteriors the benefit of the natural gradient method is especially pronounced, and we demonstrate a practical setting where ordinary gradients are unusable. We show how natural gradients can be computed efficiently and automatically in any parameterization, using automatic differentiation. Our code is integrated into the GPflow package.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge