Recommendations for Baselines and Benchmarking Approximate Gaussian Processes

Gaussian processes (GPs) are a mature and widely-used component of the ML toolbox. One of their desirable qualities is automatic hyperparameter selection, which allows for training without user intervention. However, in many realistic settings, approximations are typically needed, which typically do require tuning. We argue that this requirement for tuning complicates evaluation, which has led to a lack of a clear recommendations on which method should be used in which situation. To address this, we make recommendations for comparing GP approximations based on a specification of what a user should expect from a method. In addition, we develop a training procedure for the variational method of Titsias [2009] that leaves no choices to the user, and show that this is a strong baseline that meets our specification. We conclude that benchmarking according to our suggestions gives a clearer view of the current state of the field, and uncovers problems that are still open that future papers should address.

Trieste: Efficiently Exploring The Depths of Black-box Functions with TensorFlow

We present Trieste, an open-source Python package for Bayesian optimization and active learning benefiting from the scalability and efficiency of TensorFlow. Our library enables the plug-and-play of popular TensorFlow-based models within sequential decision-making loops, e.g. Gaussian processes from GPflow or GPflux, or neural networks from Keras. This modular mindset is central to the package and extends to our acquisition functions and the internal dynamics of the decision-making loop, both of which can be tailored and extended by researchers or engineers when tackling custom use cases. Trieste is a research-friendly and production-ready toolkit backed by a comprehensive test suite, extensive documentation, and available at https://github.com/secondmind-labs/trieste.

Numerically Stable Sparse Gaussian Processes via Minimum Separation using Cover Trees

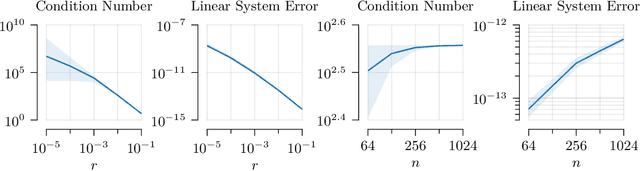
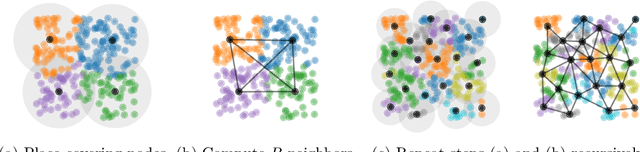
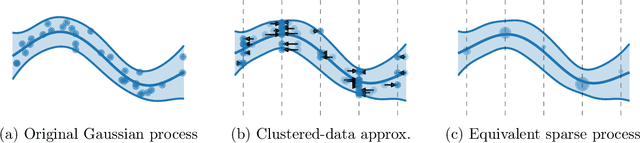
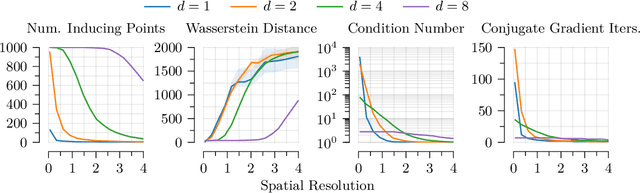
As Gaussian processes mature, they are increasingly being deployed as part of larger machine learning and decision-making systems, for instance in geospatial modeling, Bayesian optimization, or in latent Gaussian models. Within a system, the Gaussian process model needs to perform in a stable and reliable manner to ensure it interacts correctly with other parts the system. In this work, we study the numerical stability of scalable sparse approximations based on inducing points. We derive sufficient and in certain cases necessary conditions on the inducing points for the computations performed to be numerically stable. For low-dimensional tasks such as geospatial modeling, we propose an automated method for computing inducing points satisfying these conditions. This is done via a modification of the cover tree data structure, which is of independent interest. We additionally propose an alternative sparse approximation for regression with a Gaussian likelihood which trades off a small amount of performance to further improve stability. We evaluate the proposed techniques on a number of examples, showing that, in geospatial settings, sparse approximations with guaranteed numerical stability often perform comparably to those without.

Memory Safe Computations with XLA Compiler

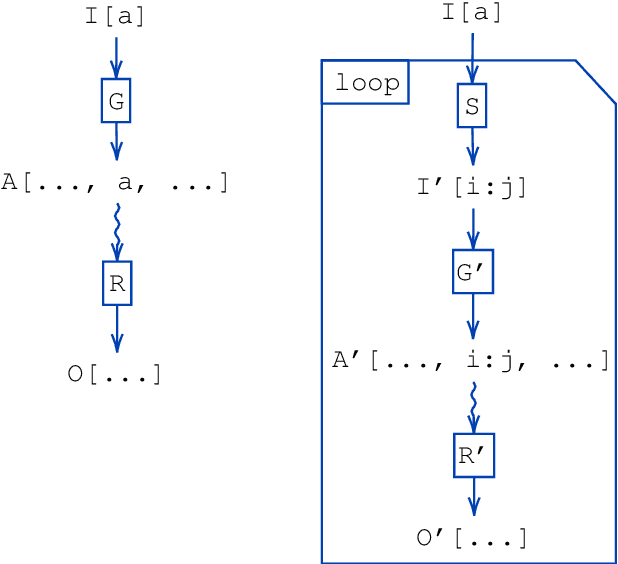
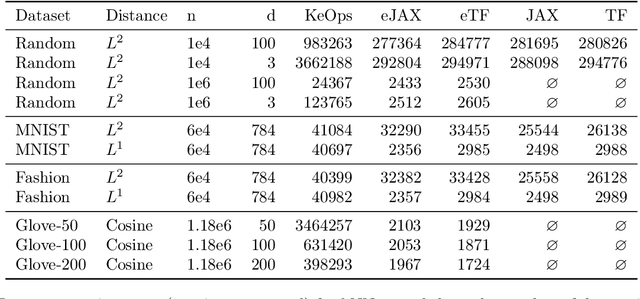
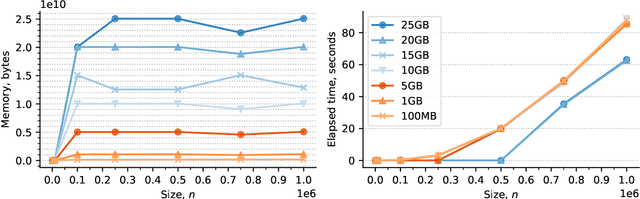
Software packages like TensorFlow and PyTorch are designed to support linear algebra operations, and their speed and usability determine their success. However, by prioritising speed, they often neglect memory requirements. As a consequence, the implementations of memory-intensive algorithms that are convenient in terms of software design can often not be run for large problems due to memory overflows. Memory-efficient solutions require complex programming approaches with significant logic outside the computational framework. This impairs the adoption and use of such algorithms. To address this, we developed an XLA compiler extension that adjusts the computational data-flow representation of an algorithm according to a user-specified memory limit. We show that k-nearest neighbour and sparse Gaussian process regression methods can be run at a much larger scale on a single device, where standard implementations would have failed. Our approach leads to better use of hardware resources. We believe that further focus on removing memory constraints at a compiler level will widen the range of machine learning methods that can be developed in the future.

Barely Biased Learning for Gaussian Process Regression

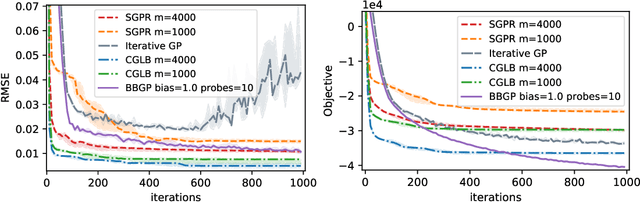
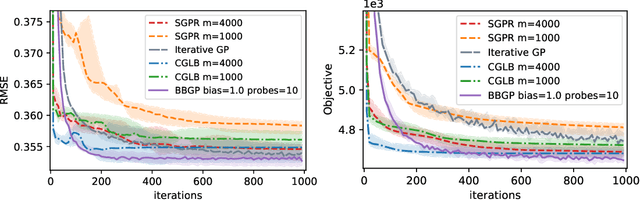
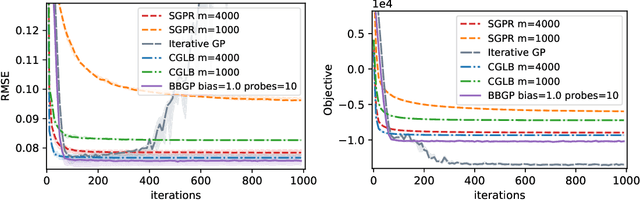
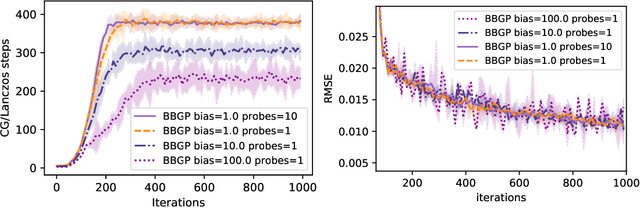
Recent work in scalable approximate Gaussian process regression has discussed a bias-variance-computation trade-off when estimating the log marginal likelihood. We suggest a method that adaptively selects the amount of computation to use when estimating the log marginal likelihood so that the bias of the objective function is guaranteed to be small. While simple in principle, our current implementation of the method is not competitive computationally with existing approximations.

GPflux: A Library for Deep Gaussian Processes

We introduce GPflux, a Python library for Bayesian deep learning with a strong emphasis on deep Gaussian processes (DGPs). Implementing DGPs is a challenging endeavour due to the various mathematical subtleties that arise when dealing with multivariate Gaussian distributions and the complex bookkeeping of indices. To date, there are no actively maintained, open-sourced and extendable libraries available that support research activities in this area. GPflux aims to fill this gap by providing a library with state-of-the-art DGP algorithms, as well as building blocks for implementing novel Bayesian and GP-based hierarchical models and inference schemes. GPflux is compatible with and built on top of the Keras deep learning eco-system. This enables practitioners to leverage tools from the deep learning community for building and training customised Bayesian models, and create hierarchical models that consist of Bayesian and standard neural network layers in a single coherent framework. GPflux relies on GPflow for most of its GP objects and operations, which makes it an efficient, modular and extensible library, while having a lean codebase.

Tighter Bounds on the Log Marginal Likelihood of Gaussian Process Regression Using Conjugate Gradients

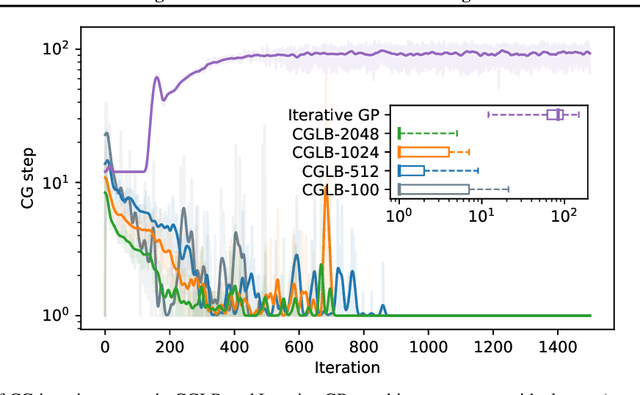
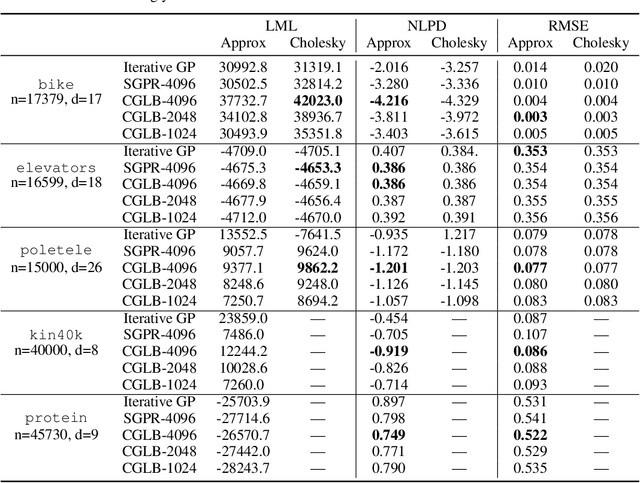
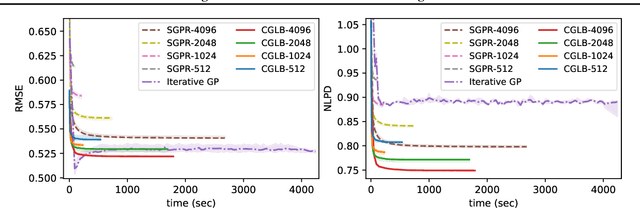
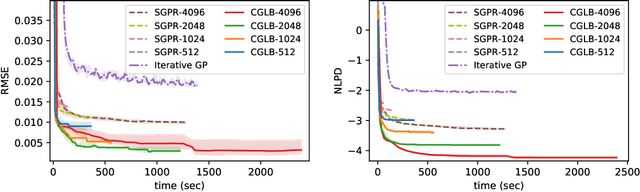
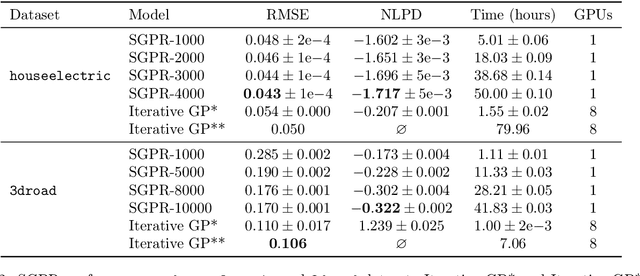
We propose a lower bound on the log marginal likelihood of Gaussian process regression models that can be computed without matrix factorisation of the full kernel matrix. We show that approximate maximum likelihood learning of model parameters by maximising our lower bound retains many of the sparse variational approach benefits while reducing the bias introduced into parameter learning. The basis of our bound is a more careful analysis of the log-determinant term appearing in the log marginal likelihood, as well as using the method of conjugate gradients to derive tight lower bounds on the term involving a quadratic form. Our approach is a step forward in unifying methods relying on lower bound maximisation (e.g. variational methods) and iterative approaches based on conjugate gradients for training Gaussian processes. In experiments, we show improved predictive performance with our model for a comparable amount of training time compared to other conjugate gradient based approaches.

Automatic Tuning of Stochastic Gradient Descent with Bayesian Optimisation

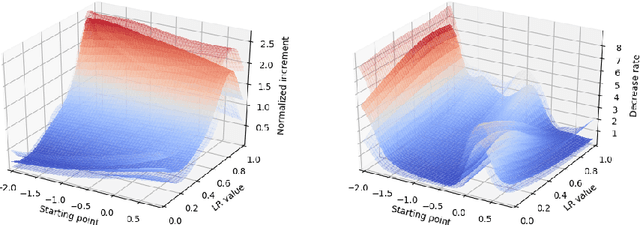
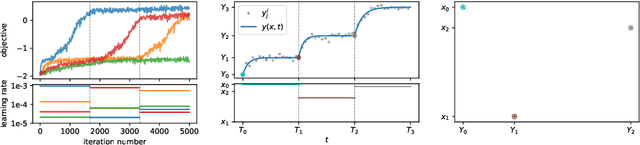
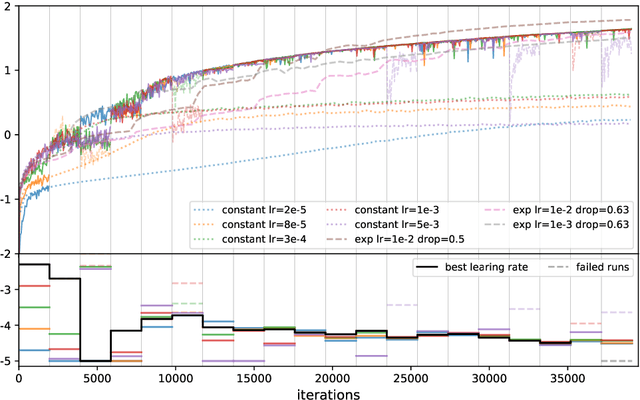
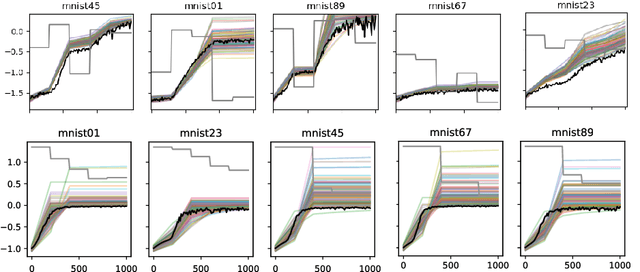
Many machine learning models require a training procedure based on running stochastic gradient descent. A key element for the efficiency of those algorithms is the choice of the learning rate schedule. While finding good learning rates schedules using Bayesian optimisation has been tackled by several authors, adapting it dynamically in a data-driven way is an open question. This is of high practical importance to users that need to train a single, expensive model. To tackle this problem, we introduce an original probabilistic model for traces of optimisers, based on latent Gaussian processes and an auto-/regressive formulation, that flexibly adjusts to abrupt changes of behaviours induced by new learning rate values. As illustrated, this model is well-suited to tackle a set of problems: first, for the on-line adaptation of the learning rate for a cold-started run; then, for tuning the schedule for a set of similar tasks (in a classical BO setup), as well as warm-starting it for a new task.

Scalable Thompson Sampling using Sparse Gaussian Process Models

Thompson Sampling (TS) with Gaussian Process (GP) models is a powerful tool for optimizing non-convex objective functions. Despite favourable theoretical properties, the computational complexity of the standard algorithms quickly becomes prohibitive as the number of observation points grows. Scalable TS methods can be implemented using sparse GP models, but at the price of an approximation error that invalidates the existing regret bounds. Here, we prove regret bounds for TS based on approximate GP posteriors, whose application to sparse GPs shows a drastic improvement in computational complexity with no loss in terms of the order of regret performance. In addition, an immediate implication of our results is an improved regret bound for the exact GP-TS. Specifically, we show an $\tilde{O}(\sqrt{\gamma_T T})$ bound on regret that is an $O(\sqrt{\gamma_T})$ improvement over the existing results where $T$ is the time horizon and $\gamma_T$ is an upper bound on the information gain. This improvement is important to ensure sublinear regret bounds.

A Framework for Interdomain and Multioutput Gaussian Processes

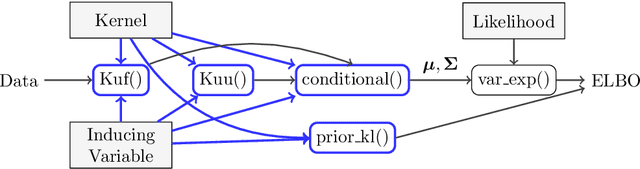
One obstacle to the use of Gaussian processes (GPs) in large-scale problems, and as a component in deep learning system, is the need for bespoke derivations and implementations for small variations in the model or inference. In order to improve the utility of GPs we need a modular system that allows rapid implementation and testing, as seen in the neural network community. We present a mathematical and software framework for scalable approximate inference in GPs, which combines interdomain approximations and multiple outputs. Our framework, implemented in GPflow, provides a unified interface for many existing multioutput models, as well as more recent convolutional structures. This simplifies the creation of deep models with GPs, and we hope that this work will encourage more interest in this approach.