Numerically Stable Sparse Gaussian Processes via Minimum Separation using Cover Trees

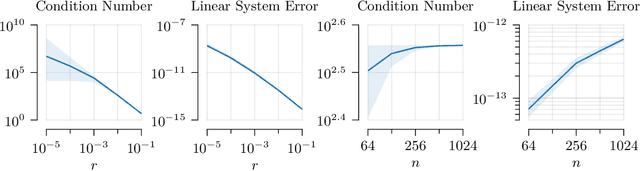
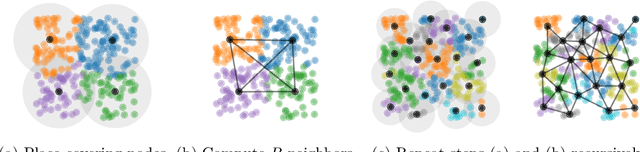
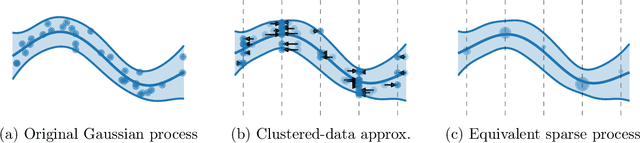
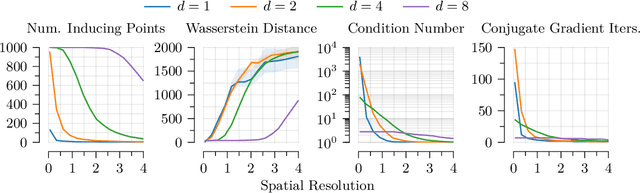
As Gaussian processes mature, they are increasingly being deployed as part of larger machine learning and decision-making systems, for instance in geospatial modeling, Bayesian optimization, or in latent Gaussian models. Within a system, the Gaussian process model needs to perform in a stable and reliable manner to ensure it interacts correctly with other parts the system. In this work, we study the numerical stability of scalable sparse approximations based on inducing points. We derive sufficient and in certain cases necessary conditions on the inducing points for the computations performed to be numerically stable. For low-dimensional tasks such as geospatial modeling, we propose an automated method for computing inducing points satisfying these conditions. This is done via a modification of the cover tree data structure, which is of independent interest. We additionally propose an alternative sparse approximation for regression with a Gaussian likelihood which trades off a small amount of performance to further improve stability. We evaluate the proposed techniques on a number of examples, showing that, in geospatial settings, sparse approximations with guaranteed numerical stability often perform comparably to those without.