Beyond Intuition, a Framework for Applying GPs to Real-World Data

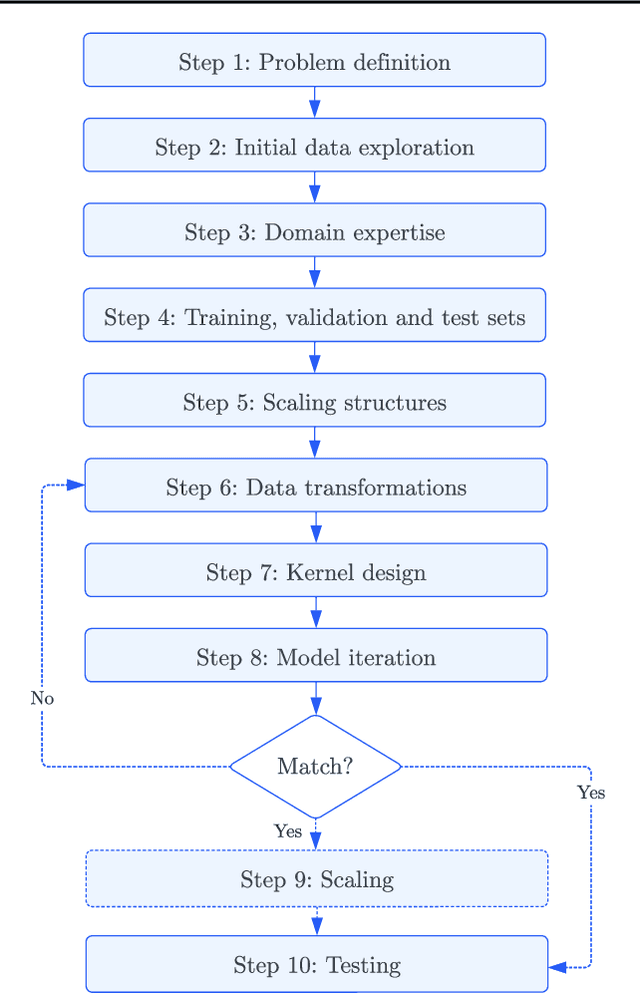
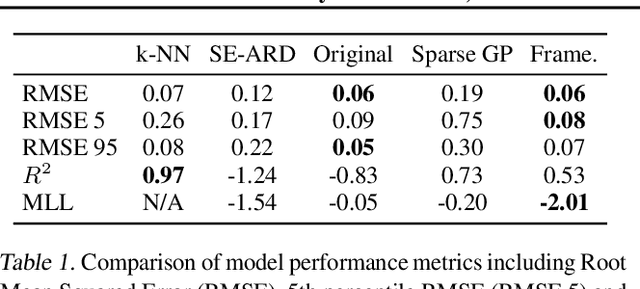
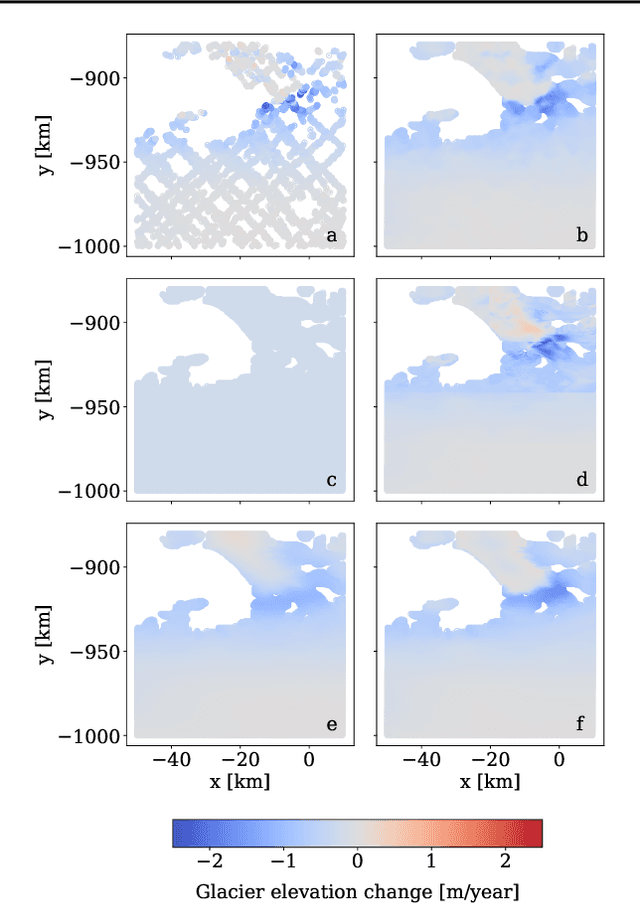
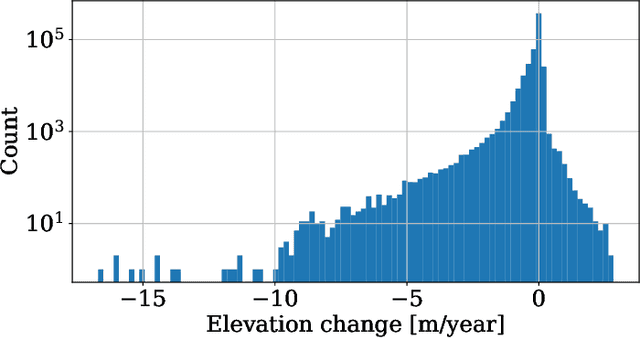
Gaussian Processes (GPs) offer an attractive method for regression over small, structured and correlated datasets. However, their deployment is hindered by computational costs and limited guidelines on how to apply GPs beyond simple low-dimensional datasets. We propose a framework to identify the suitability of GPs to a given problem and how to set up a robust and well-specified GP model. The guidelines formalise the decisions of experienced GP practitioners, with an emphasis on kernel design and options for computational scalability. The framework is then applied to a case study of glacier elevation change yielding more accurate results at test time.

Bayesian inference and neural estimation of acoustic wave propagation

In this work, we introduce a novel framework which combines physics and machine learning methods to analyse acoustic signals. Three methods are developed for this task: a Bayesian inference approach for inferring the spectral acoustics characteristics, a neural-physical model which equips a neural network with forward and backward physical losses, and the non-linear least squares approach which serves as benchmark. The inferred propagation coefficient leads to the room impulse response (RIR) quantity which can be used for relocalisation with uncertainty. The simplicity and efficiency of this framework is empirically validated on simulated data.

Neural Characteristic Activation Value Analysis for Improved ReLU Network Feature Learning

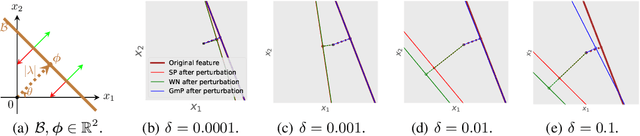
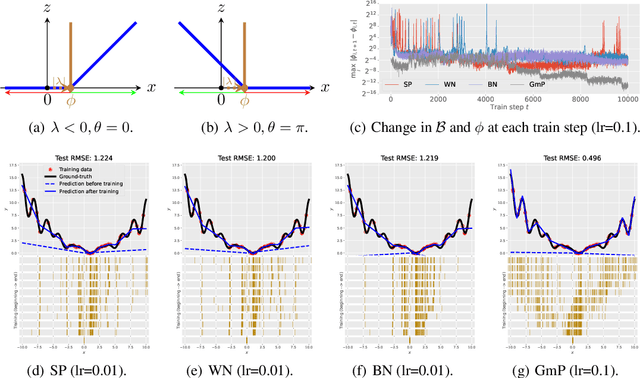
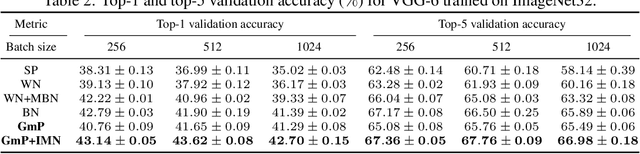
We examine the characteristic activation values of individual ReLU units in neural networks. We refer to the corresponding set for such characteristic activation values in the input space as the characteristic activation set of a ReLU unit. We draw an explicit connection between the characteristic activation set and learned features in ReLU networks. This connection leads to new insights into why various neural network normalization techniques used in modern deep learning architectures regularize and stabilize SGD optimization. Utilizing these insights, we propose a geometric approach to parameterize ReLU networks for improved feature learning. We empirically verify its usefulness with less carefully chosen initialization schemes and larger learning rates. We report improved optimization stability, faster convergence speed, and better generalization performance.

Learning Deep Neural Networks by Iterative Linearisation

The excellent real-world performance of deep neural networks has received increasing attention. Despite the capacity to overfit significantly, such large models work better than smaller ones. This phenomenon is often referred to as the scaling law by practitioners. It is of fundamental interest to study why the scaling law exists and how it avoids/controls overfitting. One approach has been looking at infinite width limits of neural networks (e.g., Neural Tangent Kernels, Gaussian Processes); however, in practise, these do not fully explain finite networks as their infinite counterparts do not learn features. Furthermore, the empirical kernel for finite networks (i.e., the inner product of feature vectors), changes significantly during training in contrast to infinite width networks. In this work we derive an iterative linearised training method. We justify iterative lineralisation as an interpolation between finite analogs of the infinite width regime, which do not learn features, and standard gradient descent training which does. We show some preliminary results where iterative linearised training works well, noting in particular how much feature learning is required to achieve comparable performance. We also provide novel insights into the training behaviour of neural networks.

Coarse-Super-Resolution-Fine Network (CoSF-Net): A Unified End-to-End Neural Network for 4D-MRI with Simultaneous Motion Estimation and Super-Resolution

Four-dimensional magnetic resonance imaging (4D-MRI) is an emerging technique for tumor motion management in image-guided radiation therapy (IGRT). However, current 4D-MRI suffers from low spatial resolution and strong motion artifacts owing to the long acquisition time and patients' respiratory variations; these limitations, if not managed properly, can adversely affect treatment planning and delivery in IGRT. Herein, we developed a novel deep learning framework called the coarse-super-resolution-fine network (CoSF-Net) to achieve simultaneous motion estimation and super-resolution in a unified model. We designed CoSF-Net by fully excavating the inherent properties of 4D-MRI, with consideration of limited and imperfectly matched training datasets. We conducted extensive experiments on multiple real patient datasets to verify the feasibility and robustness of the developed network. Compared with existing networks and three state-of-the-art conventional algorithms, CoSF-Net not only accurately estimated the deformable vector fields between the respiratory phases of 4D-MRI but also simultaneously improved the spatial resolution of 4D-MRI with enhanced anatomic features, yielding 4D-MR images with high spatiotemporal resolution.

Numerically Stable Sparse Gaussian Processes via Minimum Separation using Cover Trees

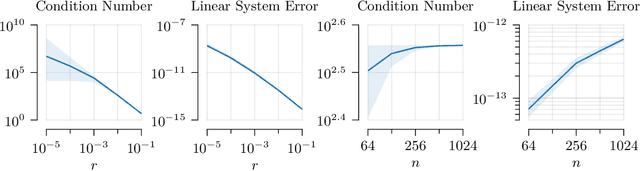
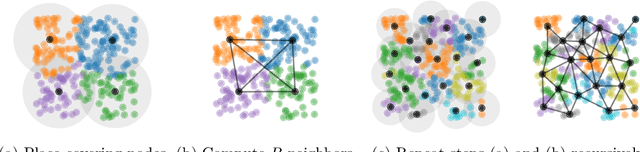
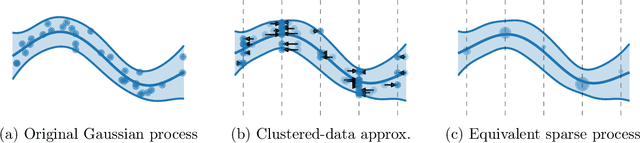
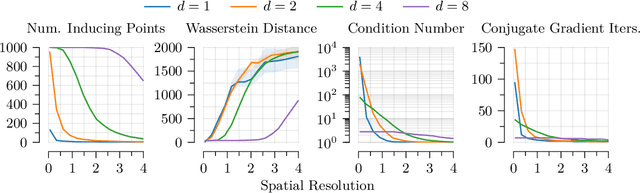
As Gaussian processes mature, they are increasingly being deployed as part of larger machine learning and decision-making systems, for instance in geospatial modeling, Bayesian optimization, or in latent Gaussian models. Within a system, the Gaussian process model needs to perform in a stable and reliable manner to ensure it interacts correctly with other parts the system. In this work, we study the numerical stability of scalable sparse approximations based on inducing points. We derive sufficient and in certain cases necessary conditions on the inducing points for the computations performed to be numerically stable. For low-dimensional tasks such as geospatial modeling, we propose an automated method for computing inducing points satisfying these conditions. This is done via a modification of the cover tree data structure, which is of independent interest. We additionally propose an alternative sparse approximation for regression with a Gaussian likelihood which trades off a small amount of performance to further improve stability. We evaluate the proposed techniques on a number of examples, showing that, in geospatial settings, sparse approximations with guaranteed numerical stability often perform comparably to those without.

DynamicPPL: Stan-like Speed for Dynamic Probabilistic Models

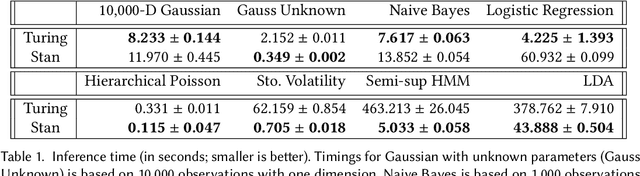
We present the preliminary high-level design and features of DynamicPPL.jl, a modular library providing a lightning-fast infrastructure for probabilistic programming. Besides a computational performance that is often close to or better than Stan, DynamicPPL provides an intuitive DSL that allows the rapid development of complex dynamic probabilistic programs. Being entirely written in Julia, a high-level dynamic programming language for numerical computing, DynamicPPL inherits a rich set of features available through the Julia ecosystem. Since DynamicPPL is a modular, stand-alone library, any probabilistic programming system written in Julia, such as Turing.jl, can use DynamicPPL to specify models and trace their model parameters. The main features of DynamicPPL are: 1) a meta-programming based DSL for specifying dynamic models using an intuitive tilde-based notation; 2) a tracing data-structure for tracking RVs in dynamic probabilistic models; 3) a rich contextual dispatch system allowing tailored behaviour during model execution; and 4) a user-friendly syntax for probabilistic queries. Finally, we show in a variety of experiments that DynamicPPL, in combination with Turing.jl, achieves computational performance that is often close to or better than Stan.

Bayesian Learning of Sum-Product Networks

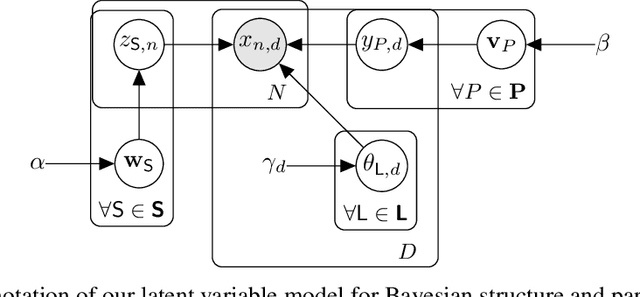
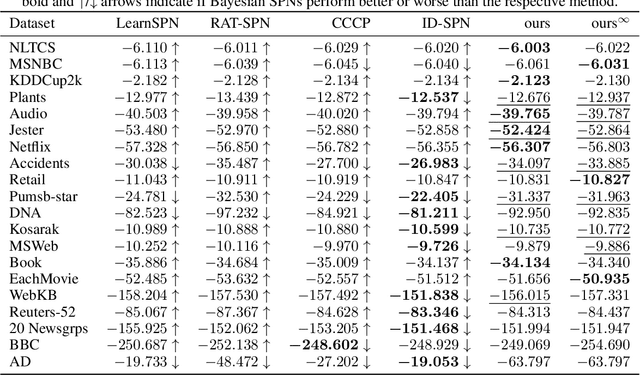
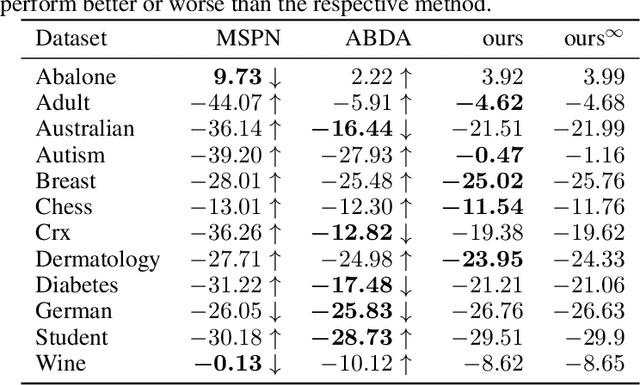
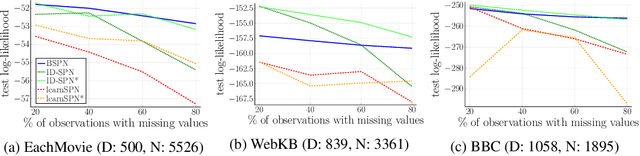
Sum-product networks (SPNs) are flexible density estimators and have received significant attention, due to their attractive inference properties. While parameter learning in SPNs is well developed, structure learning leaves something to be desired: Even though there is a plethora of SPN structure learners, most of them are somewhat ad-hoc, and based on intuition rather than a clear learning principle. In this paper, we introduce a well-principled Bayesian framework for SPN structure learning. First, we decompose the problem into i) laying out a basic computational graph, and ii) learning the so-called scope function over the graph. The first is rather unproblematic and akin to neural network architecture validation. The second characterises the effective structure of the SPN and needs to respect the usual structural constraints in SPN, i.e. completeness and decomposability. While representing and learning the scope function is rather involved in general, in this paper, we propose a natural parametrisation for an important and widely used special case of SPNs. These structural parameters are incorporated into a Bayesian model, such that simultaneous structure and parameter learning is cast into monolithic Bayesian posterior inference. In various experiments, our Bayesian SPNs often improve test likelihoods over greedy SPN learners. Further, since the Bayesian framework protects against overfitting, we are able to evaluate hyper-parameters directly on the Bayesian model score, waiving the need for a separate validation set, which is especially beneficial in low data regimes. Bayesian SPNs can be applied to heterogeneous domains and can easily be extended to nonparametric formulations. Moreover, our Bayesian approach is the first which consistently and robustly learns SPN structures under missing data.

Dirichlet Fragmentation Processes

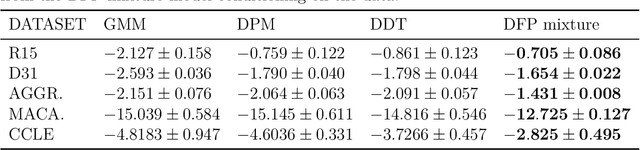
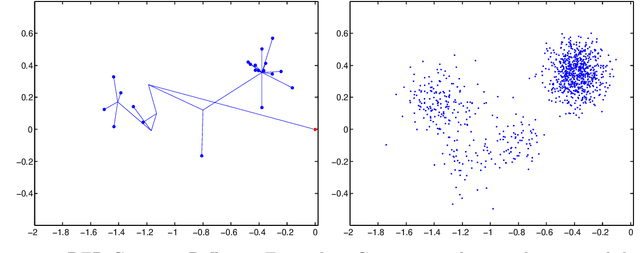
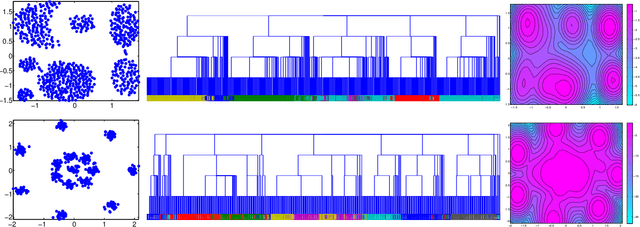
Tree structures are ubiquitous in data across many domains, and many datasets are naturally modelled by unobserved tree structures. In this paper, first we review the theory of random fragmentation processes [Bertoin, 2006], and a number of existing methods for modelling trees, including the popular nested Chinese restaurant process (nCRP). Then we define a general class of probability distributions over trees: the Dirichlet fragmentation process (DFP) through a novel combination of the theory of Dirichlet processes and random fragmentation processes. This DFP presents a stick-breaking construction, and relates to the nCRP in the same way the Dirichlet process relates to the Chinese restaurant process. Furthermore, we develop a novel hierarchical mixture model with the DFP, and empirically compare the new model to similar models in machine learning. Experiments show the DFP mixture model to be convincingly better than existing state-of-the-art approaches for hierarchical clustering and density modelling.

A Linear-Time Particle Gibbs Sampler for Infinite Hidden Markov Models

Infinite Hidden Markov Models (iHMM's) are an attractive, nonparametric generalization of the classical Hidden Markov Model which can automatically infer the number of hidden states in the system. However, due to the infinite-dimensional nature of transition dynamics performing inference in the iHMM is difficult. In this paper, we present an infinite-state Particle Gibbs (PG) algorithm to resample state trajectories for the iHMM. The proposed algorithm uses an efficient proposal optimized for iHMMs and leverages ancestor sampling to suppress degeneracy of the standard PG algorithm. Our algorithm demonstrates significant convergence improvements on synthetic and real world data sets. Additionally, the infinite-state PG algorithm has linear-time complexity in the number of states in the sampler, while competing methods scale quadratically.