Integrated Variational Fourier Features for Fast Spatial Modelling with Gaussian Processes

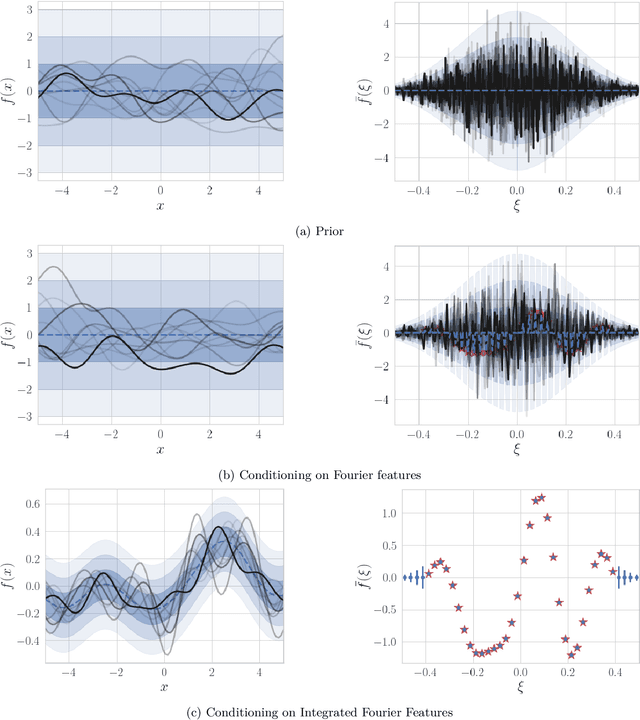
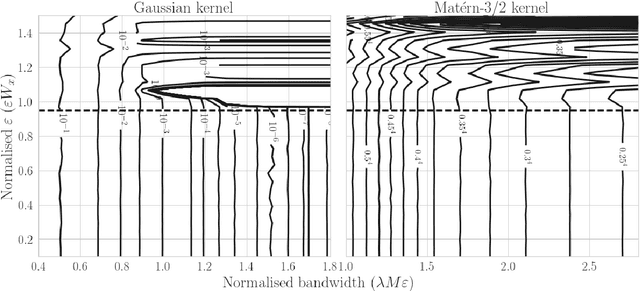
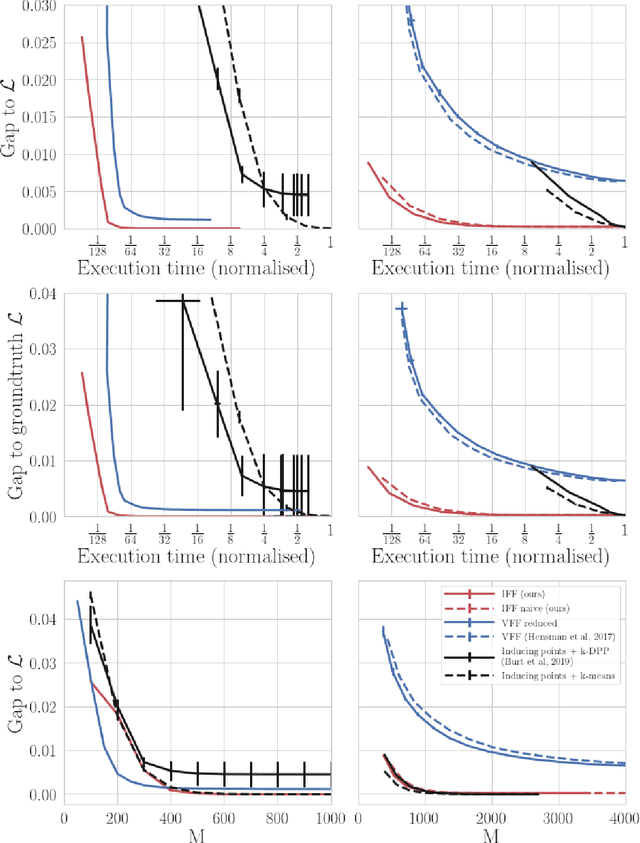
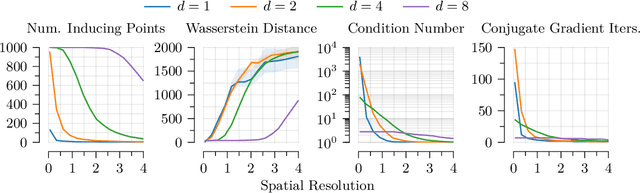
Sparse variational approximations are popular methods for scaling up inference and learning in Gaussian processes to larger datasets. For $N$ training points, exact inference has $O(N^3)$ cost; with $M \ll N$ features, state of the art sparse variational methods have $O(NM^2)$ cost. Recently, methods have been proposed using more sophisticated features; these promise $O(M^3)$ cost, with good performance in low dimensional tasks such as spatial modelling, but they only work with a very limited class of kernels, excluding some of the most commonly used. In this work, we propose integrated Fourier features, which extends these performance benefits to a very broad class of stationary covariance functions. We motivate the method and choice of parameters from a convergence analysis and empirical exploration, and show practical speedup in synthetic and real world spatial regression tasks.

Numerically Stable Sparse Gaussian Processes via Minimum Separation using Cover Trees

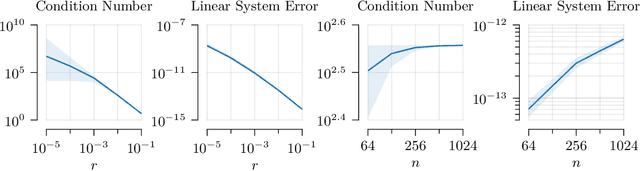
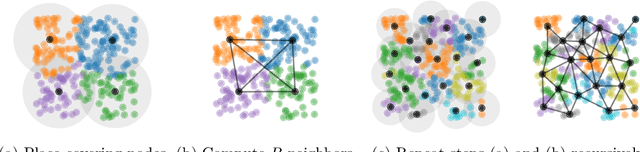
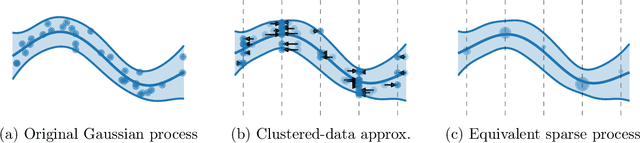
As Gaussian processes mature, they are increasingly being deployed as part of larger machine learning and decision-making systems, for instance in geospatial modeling, Bayesian optimization, or in latent Gaussian models. Within a system, the Gaussian process model needs to perform in a stable and reliable manner to ensure it interacts correctly with other parts the system. In this work, we study the numerical stability of scalable sparse approximations based on inducing points. We derive sufficient and in certain cases necessary conditions on the inducing points for the computations performed to be numerically stable. For low-dimensional tasks such as geospatial modeling, we propose an automated method for computing inducing points satisfying these conditions. This is done via a modification of the cover tree data structure, which is of independent interest. We additionally propose an alternative sparse approximation for regression with a Gaussian likelihood which trades off a small amount of performance to further improve stability. We evaluate the proposed techniques on a number of examples, showing that, in geospatial settings, sparse approximations with guaranteed numerical stability often perform comparably to those without.

Marginalised Gaussian Processes with Nested Sampling

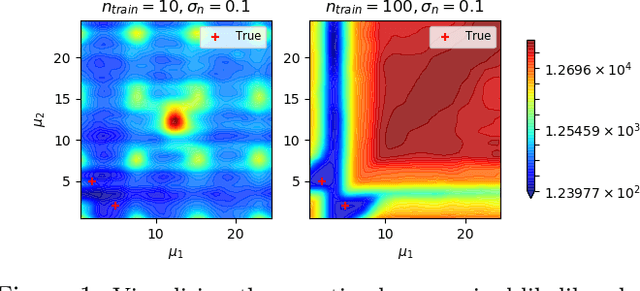
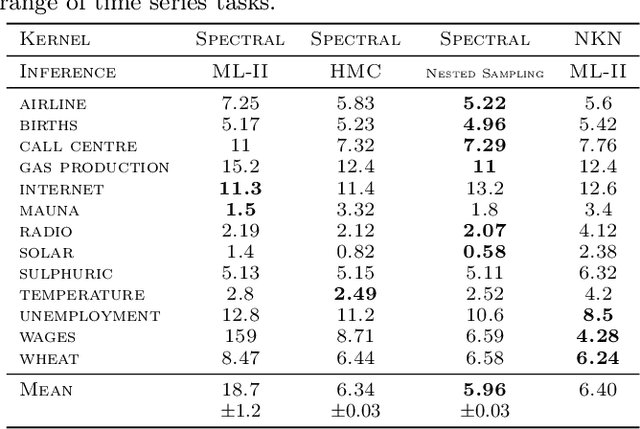
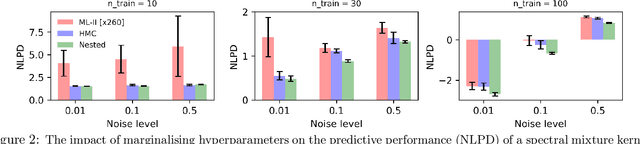
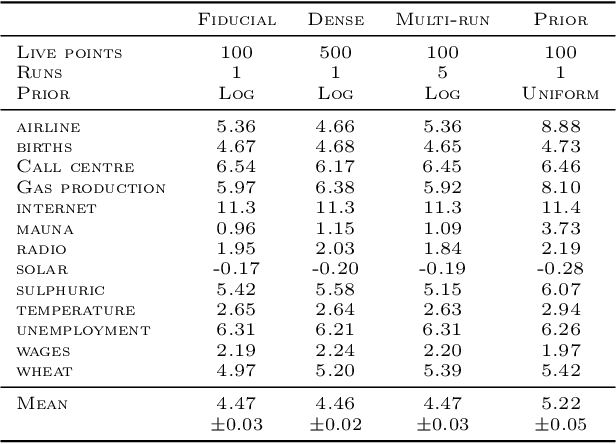
Gaussian Process (GPs) models are a rich distribution over functions with inductive biases controlled by a kernel function. Learning occurs through the optimisation of kernel hyperparameters using the marginal likelihood as the objective. This classical approach known as Type-II maximum likelihood (ML-II) yields point estimates of the hyperparameters, and continues to be the default method for training GPs. However, this approach risks underestimating predictive uncertainty and is prone to overfitting especially when there are many hyperparameters. Furthermore, gradient based optimisation makes ML-II point estimates highly susceptible to the presence of local minima. This work presents an alternative learning procedure where the hyperparameters of the kernel function are marginalised using Nested Sampling (NS), a technique that is well suited to sample from complex, multi-modal distributions. We focus on regression tasks with the spectral mixture (SM) class of kernels and find that a principled approach to quantifying model uncertainty leads to substantial gains in predictive performance across a range of synthetic and benchmark data sets. In this context, nested sampling is also found to offer a speed advantage over Hamiltonian Monte Carlo (HMC), widely considered to be the gold-standard in MCMC based inference.

Ensembling geophysical models with Bayesian Neural Networks

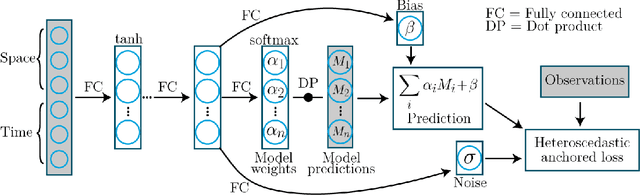
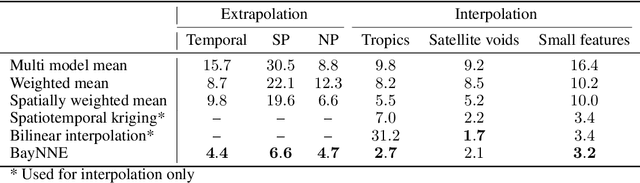
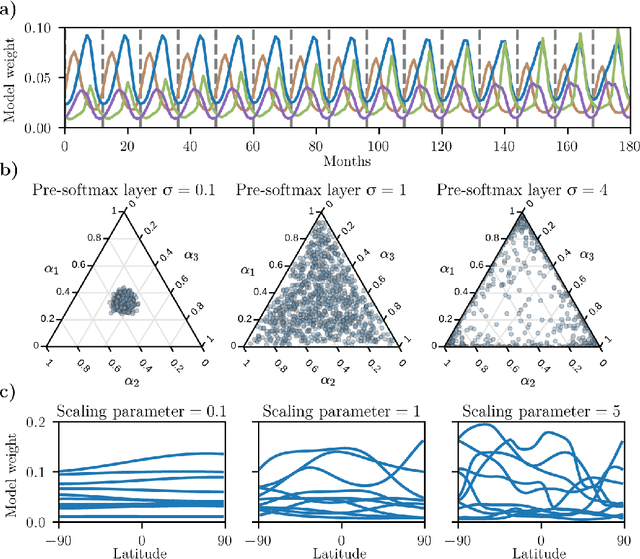
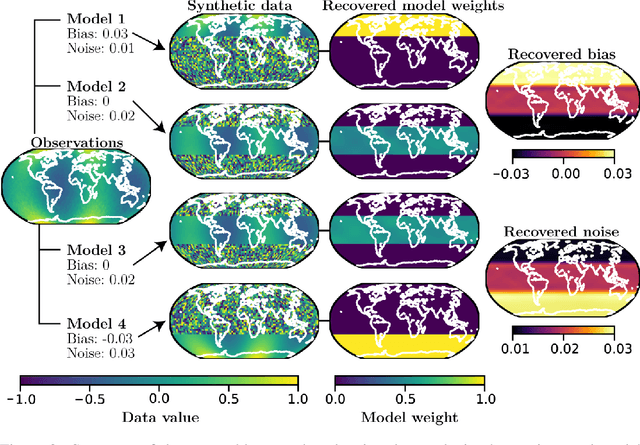
Ensembles of geophysical models improve projection accuracy and express uncertainties. We develop a novel data-driven ensembling strategy for combining geophysical models using Bayesian Neural Networks, which infers spatiotemporally varying model weights and bias while accounting for heteroscedastic uncertainties in the observations. This produces more accurate and uncertainty-aware projections without sacrificing interpretability. Applied to the prediction of total column ozone from an ensemble of 15 chemistry-climate models, we find that the Bayesian neural network ensemble (BayNNE) outperforms existing ensembling methods, achieving a 49.4% reduction in RMSE for temporal extrapolation, and a 67.4% reduction in RMSE for polar data voids, compared to a weighted mean. Uncertainty is also well-characterized, with 90.6% of the data points in our extrapolation validation dataset lying within 2 standard deviations and 98.5% within 3 standard deviations.

Convergence of Sparse Variational Inference in Gaussian Processes Regression

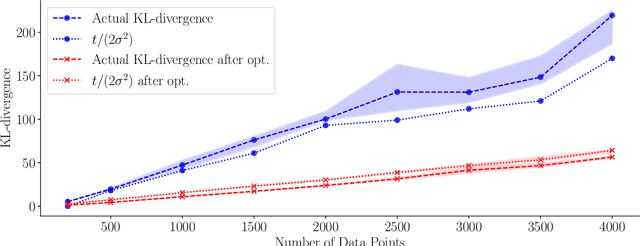
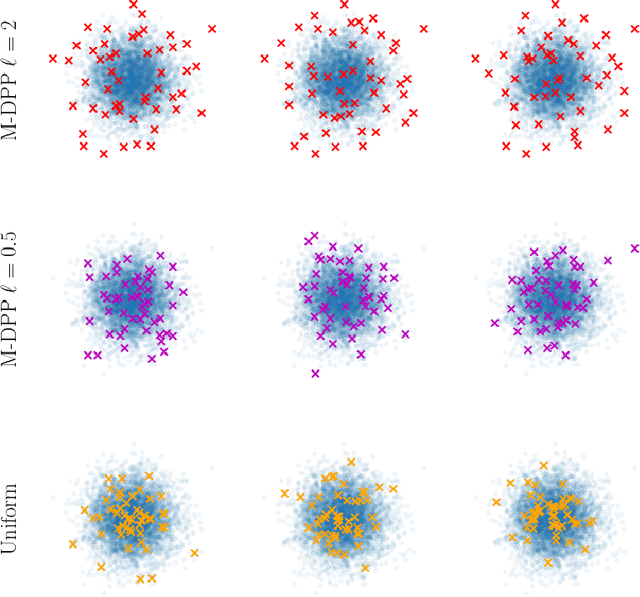
Gaussian processes are distributions over functions that are versatile and mathematically convenient priors in Bayesian modelling. However, their use is often impeded for data with large numbers of observations, $N$, due to the cubic (in $N$) cost of matrix operations used in exact inference. Many solutions have been proposed that rely on $M \ll N$ inducing variables to form an approximation at a cost of $\mathcal{O}(NM^2)$. While the computational cost appears linear in $N$, the true complexity depends on how $M$ must scale with $N$ to ensure a certain quality of the approximation. In this work, we investigate upper and lower bounds on how $M$ needs to grow with $N$ to ensure high quality approximations. We show that we can make the KL-divergence between the approximate model and the exact posterior arbitrarily small for a Gaussian-noise regression model with $M\ll N$. Specifically, for the popular squared exponential kernel and $D$-dimensional Gaussian distributed covariates, $M=\mathcal{O}((\log N)^D)$ suffice and a method with an overall computational cost of $\mathcal{O}(N(\log N)^{2D}(\log\log N)^2)$ can be used to perform inference.

Variational Orthogonal Features

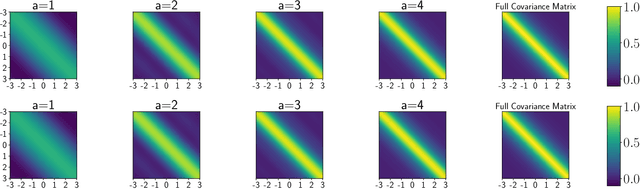
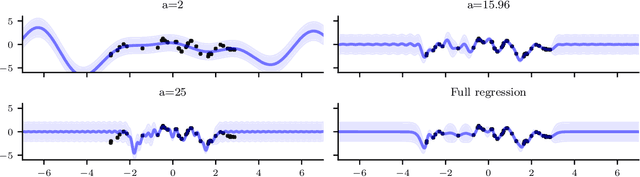
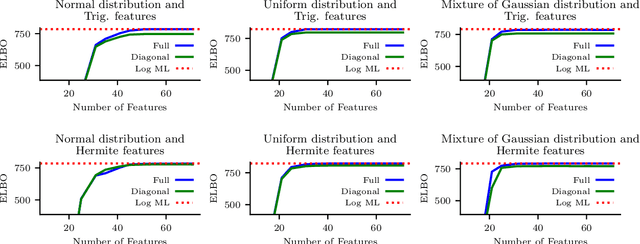
Sparse stochastic variational inference allows Gaussian process models to be applied to large datasets. The per iteration computational cost of inference with this method is $\mathcal{O}(\tilde{N}M^2+M^3),$ where $\tilde{N}$ is the number of points in a minibatch and $M$ is the number of `inducing features', which determine the expressiveness of the variational family. Several recent works have shown that for certain priors, features can be defined that remove the $\mathcal{O}(M^3)$ cost of computing a minibatch estimate of an evidence lower bound (ELBO). This represents a significant computational savings when $M\gg \tilde{N}$. We present a construction of features for any stationary prior kernel that allow for computation of an unbiased estimator to the ELBO using $T$ Monte Carlo samples in $\mathcal{O}(\tilde{N}T+M^2T)$ and in $\mathcal{O}(\tilde{N}T+MT)$ with an additional approximation. We analyze the impact of this additional approximation on inference quality.

Approximate Inference for Fully Bayesian Gaussian Process Regression

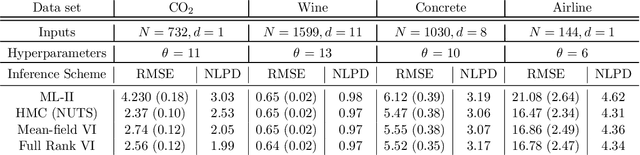
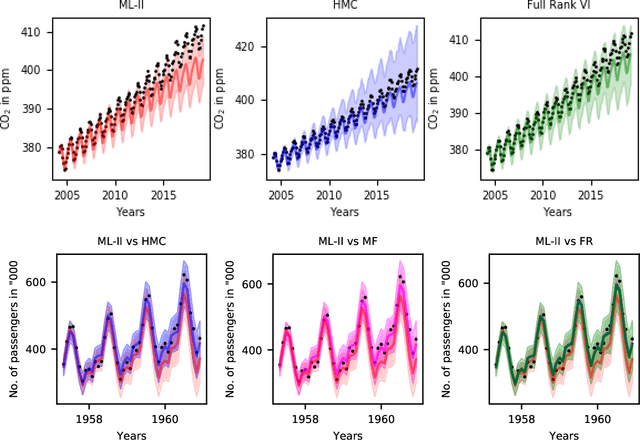
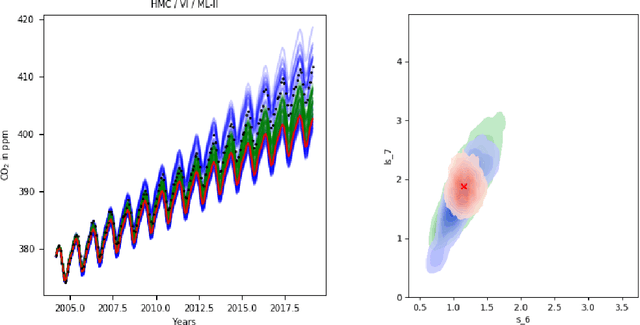
Learning in Gaussian Process models occurs through the adaptation of hyperparameters of the mean and the covariance function. The classical approach entails maximizing the marginal likelihood yielding fixed point estimates (an approach called \textit{Type II maximum likelihood} or ML-II). An alternative learning procedure is to infer the posterior over hyperparameters in a hierarchical specification of GPs we call \textit{Fully Bayesian Gaussian Process Regression} (GPR). This work considers two approximation schemes for the intractable hyperparameter posterior: 1) Hamiltonian Monte Carlo (HMC) yielding a sampling-based approximation and 2) Variational Inference (VI) where the posterior over hyperparameters is approximated by a factorized Gaussian (mean-field) or a full-rank Gaussian accounting for correlations between hyperparameters. We analyze the predictive performance for fully Bayesian GPR on a range of benchmark data sets.

Benchmarking the Neural Linear Model for Regression

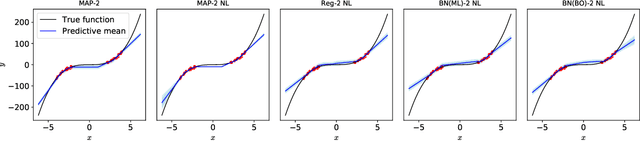
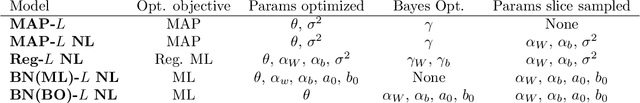
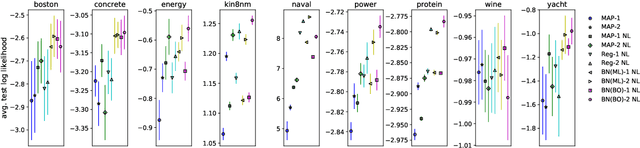
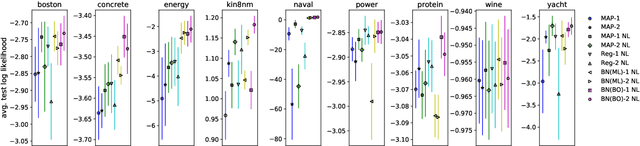
The neural linear model is a simple adaptive Bayesian linear regression method that has recently been used in a number of problems ranging from Bayesian optimization to reinforcement learning. Despite its apparent successes in these settings, to the best of our knowledge there has been no systematic exploration of its capabilities on simple regression tasks. In this work we characterize these on the UCI datasets, a popular benchmark for Bayesian regression models, as well as on the recently introduced UCI "gap" datasets, which are better tests of out-of-distribution uncertainty. We demonstrate that the neural linear model is a simple method that shows generally good performance on these tasks, but at the cost of requiring good hyperparameter tuning.

Overcoming Mean-Field Approximations in Recurrent Gaussian Process Models

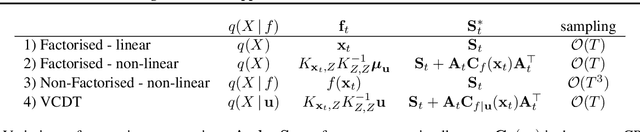
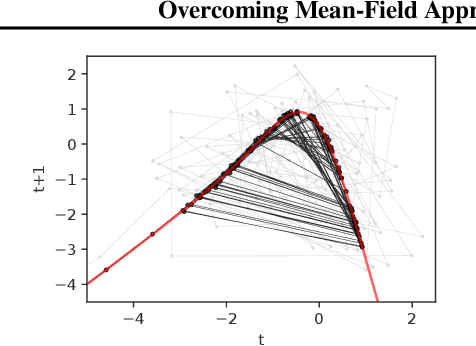
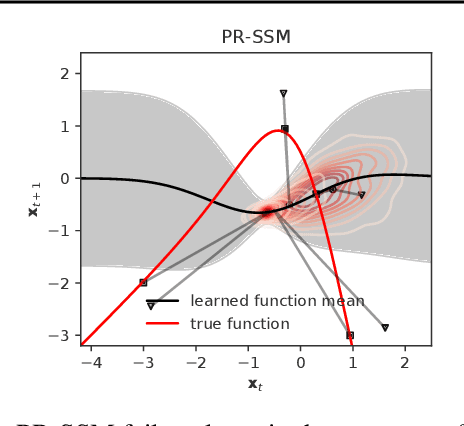
We identify a new variational inference scheme for dynamical systems whose transition function is modelled by a Gaussian process. Inference in this setting has either employed computationally intensive MCMC methods, or relied on factorisations of the variational posterior. As we demonstrate in our experiments, the factorisation between latent system states and transition function can lead to a miscalibrated posterior and to learning unnecessarily large noise terms. We eliminate this factorisation by explicitly modelling the dependence between state trajectories and the Gaussian process posterior. Samples of the latent states can then be tractably generated by conditioning on this representation. The method we obtain (VCDT: variationally coupled dynamics and trajectories) gives better predictive performance and more calibrated estimates of the transition function, yet maintains the same time and space complexities as mean-field methods. Code is available at: github.com/ialong/GPt.

PIPPS: Flexible Model-Based Policy Search Robust to the Curse of Chaos

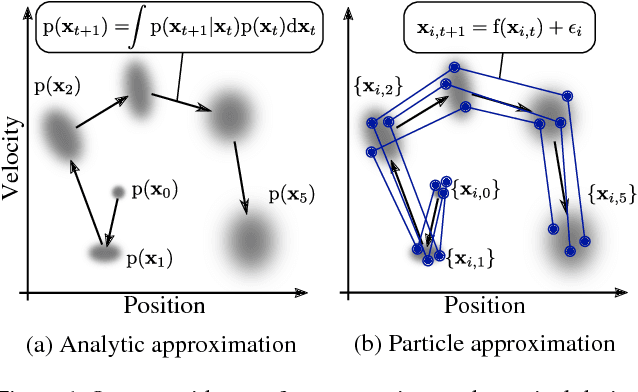
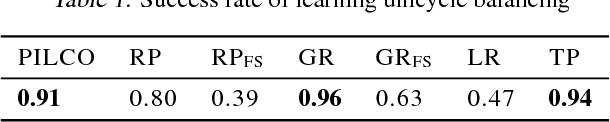
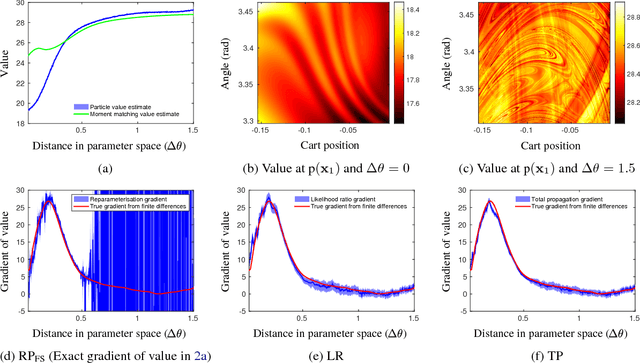
Previously, the exploding gradient problem has been explained to be central in deep learning and model-based reinforcement learning, because it causes numerical issues and instability in optimization. Our experiments in model-based reinforcement learning imply that the problem is not just a numerical issue, but it may be caused by a fundamental chaos-like nature of long chains of nonlinear computations. Not only do the magnitudes of the gradients become large, the direction of the gradients becomes essentially random. We show that reparameterization gradients suffer from the problem, while likelihood ratio gradients are robust. Using our insights, we develop a model-based policy search framework, Probabilistic Inference for Particle-Based Policy Search (PIPPS), which is easily extensible, and allows for almost arbitrary models and policies, while simultaneously matching the performance of previous data-efficient learning algorithms. Finally, we invent the total propagation algorithm, which efficiently computes a union over all pathwise derivative depths during a single backwards pass, automatically giving greater weight to estimators with lower variance, sometimes improving over reparameterization gradients by $10^6$ times.