Variational Orthogonal Features
Paper and Code
Jun 23, 2020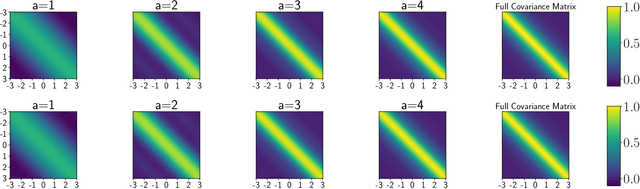
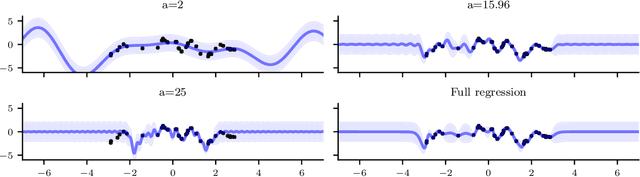
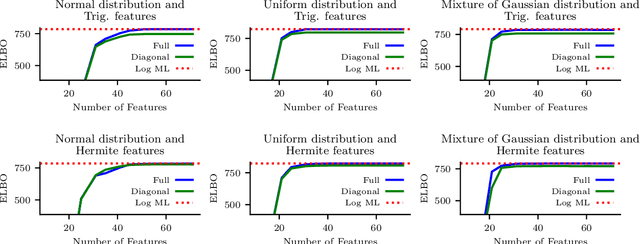
Sparse stochastic variational inference allows Gaussian process models to be applied to large datasets. The per iteration computational cost of inference with this method is $\mathcal{O}(\tilde{N}M^2+M^3),$ where $\tilde{N}$ is the number of points in a minibatch and $M$ is the number of `inducing features', which determine the expressiveness of the variational family. Several recent works have shown that for certain priors, features can be defined that remove the $\mathcal{O}(M^3)$ cost of computing a minibatch estimate of an evidence lower bound (ELBO). This represents a significant computational savings when $M\gg \tilde{N}$. We present a construction of features for any stationary prior kernel that allow for computation of an unbiased estimator to the ELBO using $T$ Monte Carlo samples in $\mathcal{O}(\tilde{N}T+M^2T)$ and in $\mathcal{O}(\tilde{N}T+MT)$ with an additional approximation. We analyze the impact of this additional approximation on inference quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge