Lipschitz-Driven Inference: Bias-corrected Confidence Intervals for Spatial Linear Models

Linear models remain ubiquitous in modern spatial applications - including climate science, public health, and economics - due to their interpretability, speed, and reproducibility. While practitioners generally report a form of uncertainty, popular spatial uncertainty quantification methods do not jointly handle model misspecification and distribution shift - despite both being essentially always present in spatial problems. In the present paper, we show that existing methods for constructing confidence (or credible) intervals in spatial linear models fail to provide correct coverage due to unaccounted-for bias. In contrast to classical methods that rely on an i.i.d. assumption that is inappropriate in spatial problems, in the present work we instead make a spatial smoothness (Lipschitz) assumption. We are then able to propose a new confidence-interval construction that accounts for bias in the estimation procedure. We demonstrate that our new method achieves nominal coverage via both theory and experiments. Code to reproduce experiments is available at https://github.com/DavidRBurt/Lipschitz-Driven-Inference.

A Framework for Evaluating PM2.5 Forecasts from the Perspective of Individual Decision Making

Wildfire frequency is increasing as the climate changes, and the resulting air pollution poses health risks. Just as people routinely use weather forecasts to plan their activities around precipitation, reliable air quality forecasts could help individuals reduce their exposure to air pollution. In the present work, we evaluate several existing forecasts of fine particular matter (PM2.5) within the continental United States in the context of individual decision-making. Our comparison suggests there is meaningful room for improvement in air pollution forecasting, which might be realized by incorporating more data sources and using machine learning tools. To facilitate future machine learning development and benchmarking, we set up a framework to evaluate and compare air pollution forecasts for individual decision making. We introduce a new loss to capture decisions about when to use mitigation measures. We highlight the importance of visualizations when comparing forecasts. Finally, we provide code to download and compare archived forecast predictions.

Consistent Validation for Predictive Methods in Spatial Settings

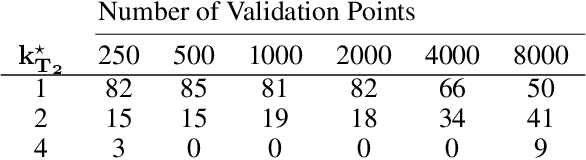
Spatial prediction tasks are key to weather forecasting, studying air pollution, and other scientific endeavors. Determining how much to trust predictions made by statistical or physical methods is essential for the credibility of scientific conclusions. Unfortunately, classical approaches for validation fail to handle mismatch between locations available for validation and (test) locations where we want to make predictions. This mismatch is often not an instance of covariate shift (as commonly formalized) because the validation and test locations are fixed (e.g., on a grid or at select points) rather than i.i.d. from two distributions. In the present work, we formalize a check on validation methods: that they become arbitrarily accurate as validation data becomes arbitrarily dense. We show that classical and covariate-shift methods can fail this check. We instead propose a method that builds from existing ideas in the covariate-shift literature, but adapts them to the validation data at hand. We prove that our proposal passes our check. And we demonstrate its advantages empirically on simulated and real data.

Gaussian processes at the Helm: A more fluid model for ocean currents

Oceanographers are interested in predicting ocean currents and identifying divergences in a current vector field based on sparse observations of buoy velocities. Since we expect current dynamics to be smooth but highly non-linear, Gaussian processes (GPs) offer an attractive model. But we show that applying a GP with a standard stationary kernel directly to buoy data can struggle at both current prediction and divergence identification -- due to some physically unrealistic prior assumptions. To better reflect known physical properties of currents, we propose to instead put a standard stationary kernel on the divergence and curl-free components of a vector field obtained through a Helmholtz decomposition. We show that, because this decomposition relates to the original vector field just via mixed partial derivatives, we can still perform inference given the original data with only a small constant multiple of additional computational expense. We illustrate the benefits of our method on synthetic and real ocean data.

Sparse Gaussian Process Hyperparameters: Optimize or Integrate?

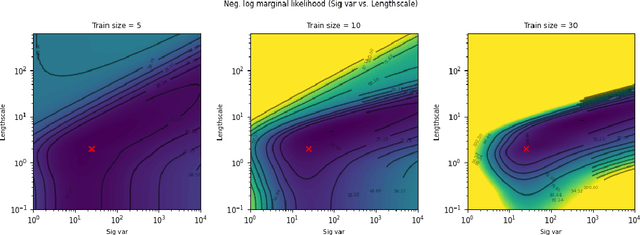
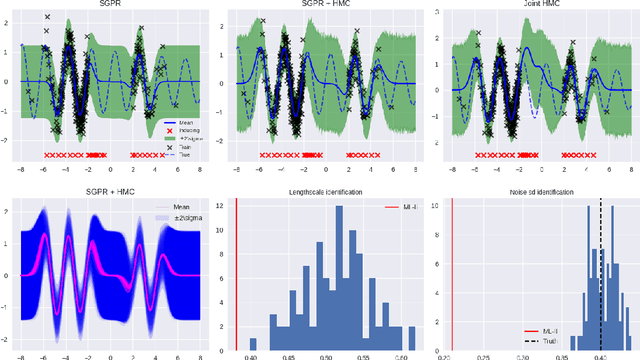
The kernel function and its hyperparameters are the central model selection choice in a Gaussian proces (Rasmussen and Williams, 2006). Typically, the hyperparameters of the kernel are chosen by maximising the marginal likelihood, an approach known as Type-II maximum likelihood (ML-II). However, ML-II does not account for hyperparameter uncertainty, and it is well-known that this can lead to severely biased estimates and an underestimation of predictive uncertainty. While there are several works which employ a fully Bayesian characterisation of GPs, relatively few propose such approaches for the sparse GPs paradigm. In this work we propose an algorithm for sparse Gaussian process regression which leverages MCMC to sample from the hyperparameter posterior within the variational inducing point framework of Titsias (2009). This work is closely related to Hensman et al. (2015b) but side-steps the need to sample the inducing points, thereby significantly improving sampling efficiency in the Gaussian likelihood case. We compare this scheme against natural baselines in literature along with stochastic variational GPs (SVGPs) along with an extensive computational analysis.

Numerically Stable Sparse Gaussian Processes via Minimum Separation using Cover Trees

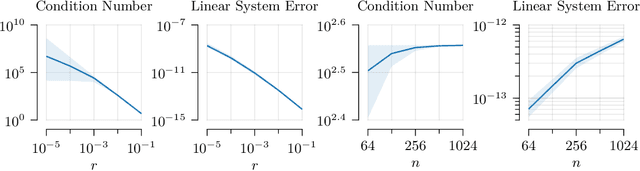
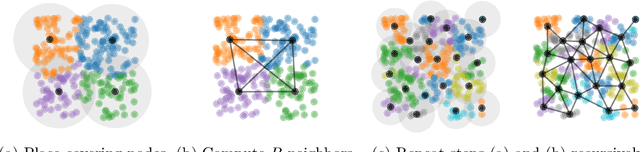
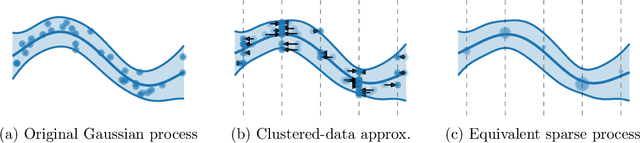
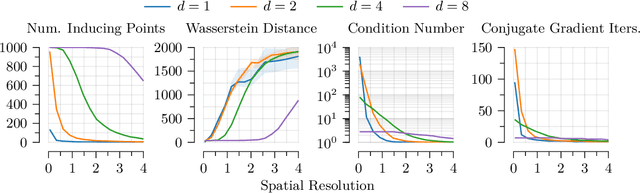
As Gaussian processes mature, they are increasingly being deployed as part of larger machine learning and decision-making systems, for instance in geospatial modeling, Bayesian optimization, or in latent Gaussian models. Within a system, the Gaussian process model needs to perform in a stable and reliable manner to ensure it interacts correctly with other parts the system. In this work, we study the numerical stability of scalable sparse approximations based on inducing points. We derive sufficient and in certain cases necessary conditions on the inducing points for the computations performed to be numerically stable. For low-dimensional tasks such as geospatial modeling, we propose an automated method for computing inducing points satisfying these conditions. This is done via a modification of the cover tree data structure, which is of independent interest. We additionally propose an alternative sparse approximation for regression with a Gaussian likelihood which trades off a small amount of performance to further improve stability. We evaluate the proposed techniques on a number of examples, showing that, in geospatial settings, sparse approximations with guaranteed numerical stability often perform comparably to those without.

A Note on the Chernoff Bound for Random Variables in the Unit Interval

The Chernoff bound is a well-known tool for obtaining a high probability bound on the expectation of a Bernoulli random variable in terms of its sample average. This bound is commonly used in statistical learning theory to upper bound the generalisation risk of a hypothesis in terms of its empirical risk on held-out data, for the case of a binary-valued loss function. However, the extension of this bound to the case of random variables taking values in the unit interval is less well known in the community. In this note we provide a proof of this extension for convenience and future reference.

Wide Mean-Field Bayesian Neural Networks Ignore the Data

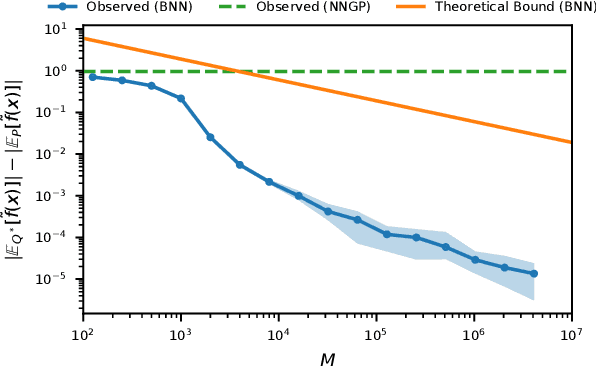
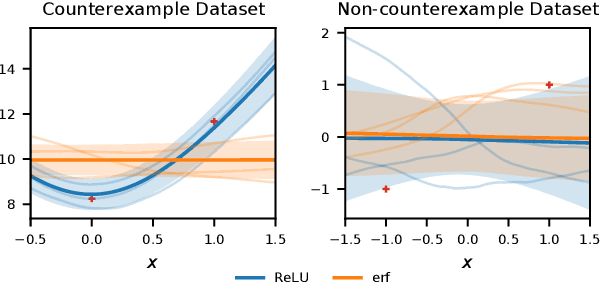
Bayesian neural networks (BNNs) combine the expressive power of deep learning with the advantages of Bayesian formalism. In recent years, the analysis of wide, deep BNNs has provided theoretical insight into their priors and posteriors. However, we have no analogous insight into their posteriors under approximate inference. In this work, we show that mean-field variational inference entirely fails to model the data when the network width is large and the activation function is odd. Specifically, for fully-connected BNNs with odd activation functions and a homoscedastic Gaussian likelihood, we show that the optimal mean-field variational posterior predictive (i.e., function space) distribution converges to the prior predictive distribution as the width tends to infinity. We generalize aspects of this result to other likelihoods. Our theoretical results are suggestive of underfitting behavior previously observered in BNNs. While our convergence bounds are non-asymptotic and constants in our analysis can be computed, they are currently too loose to be applicable in standard training regimes. Finally, we show that the optimal approximate posterior need not tend to the prior if the activation function is not odd, showing that our statements cannot be generalized arbitrarily.

Barely Biased Learning for Gaussian Process Regression

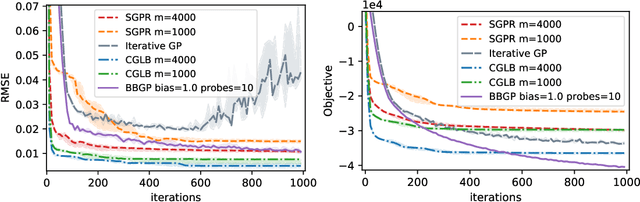
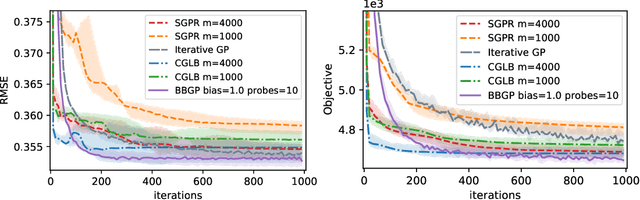
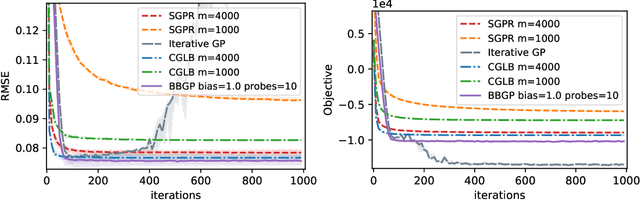
Recent work in scalable approximate Gaussian process regression has discussed a bias-variance-computation trade-off when estimating the log marginal likelihood. We suggest a method that adaptively selects the amount of computation to use when estimating the log marginal likelihood so that the bias of the objective function is guaranteed to be small. While simple in principle, our current implementation of the method is not competitive computationally with existing approximations.

How Tight Can PAC-Bayes be in the Small Data Regime?

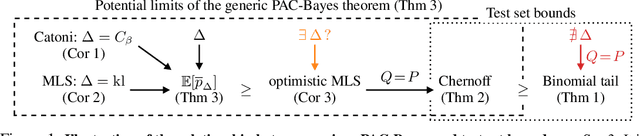
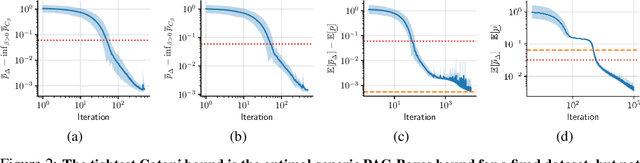
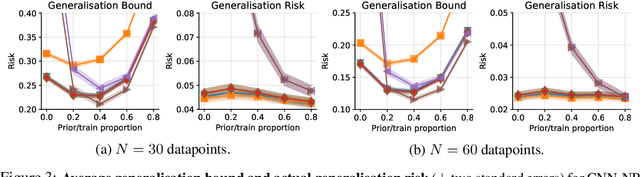
In this paper, we investigate the question: Given a small number of datapoints, for example N = 30, how tight can PAC-Bayes and test set bounds be made? For such small datasets, test set bounds adversely affect generalisation performance by discarding data. In this setting, PAC-Bayes bounds are especially attractive, due to their ability to use all the data to simultaneously learn a posterior and bound its generalisation risk. We focus on the case of i.i.d. data with a bounded loss and consider the generic PAC-Bayes theorem of Germain et al. (2009) and Begin et al. (2016). While their theorem is known to recover many existing PAC-Bayes bounds, it is unclear what the tightest bound derivable from their framework is. Surprisingly, we show that for a fixed learning algorithm and dataset, the tightest bound of this form coincides with the tightest bound of the more restrictive family of bounds considered in Catoni (2007). In contrast, in the more natural case of distributions over datasets, we give examples (both analytic and numerical) showing that the family of bounds in Catoni (2007) can be suboptimal. Within the proof framework of Germain et al. (2009) and Begin et al. (2016), we establish a lower bound on the best bound achievable in expectation, which recovers the Chernoff test set bound in the case when the posterior is equal to the prior. Finally, to illustrate how tight these bounds can potentially be, we study a synthetic one-dimensional classification task in which it is feasible to meta-learn both the prior and the form of the bound to obtain the tightest PAC-Bayes and test set bounds possible. We find that in this simple, controlled scenario, PAC-Bayes bounds are surprisingly competitive with comparable, commonly used Chernoff test set bounds. However, the sharpest test set bounds still lead to better guarantees on the generalisation error than the PAC-Bayes bounds we consider.