Lipschitz-Driven Inference: Bias-corrected Confidence Intervals for Spatial Linear Models

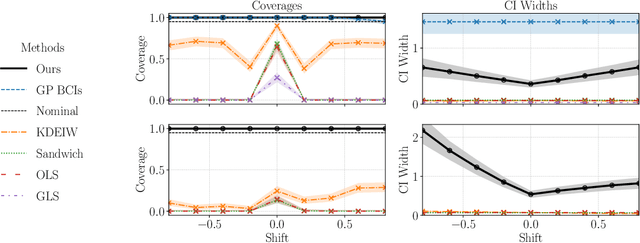
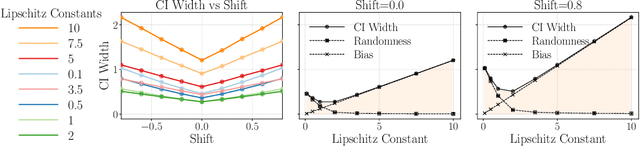
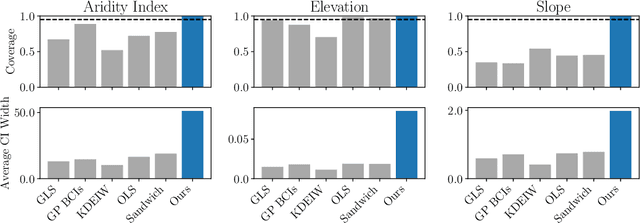
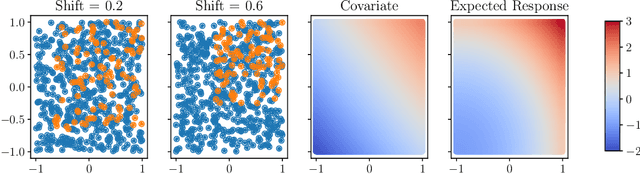
Linear models remain ubiquitous in modern spatial applications - including climate science, public health, and economics - due to their interpretability, speed, and reproducibility. While practitioners generally report a form of uncertainty, popular spatial uncertainty quantification methods do not jointly handle model misspecification and distribution shift - despite both being essentially always present in spatial problems. In the present paper, we show that existing methods for constructing confidence (or credible) intervals in spatial linear models fail to provide correct coverage due to unaccounted-for bias. In contrast to classical methods that rely on an i.i.d. assumption that is inappropriate in spatial problems, in the present work we instead make a spatial smoothness (Lipschitz) assumption. We are then able to propose a new confidence-interval construction that accounts for bias in the estimation procedure. We demonstrate that our new method achieves nominal coverage via both theory and experiments. Code to reproduce experiments is available at https://github.com/DavidRBurt/Lipschitz-Driven-Inference.