Lipschitz-Driven Inference: Bias-corrected Confidence Intervals for Spatial Linear Models

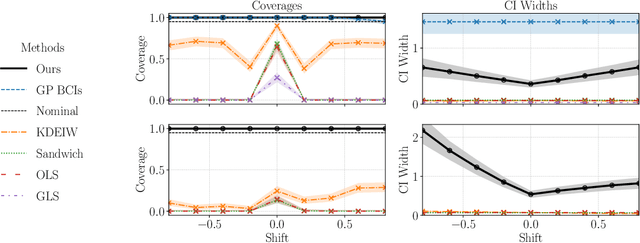
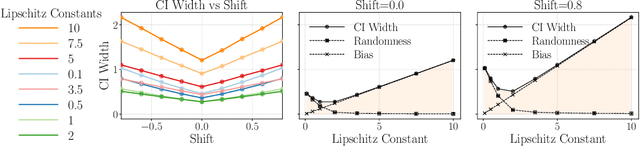
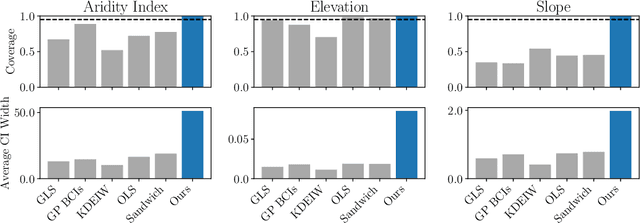
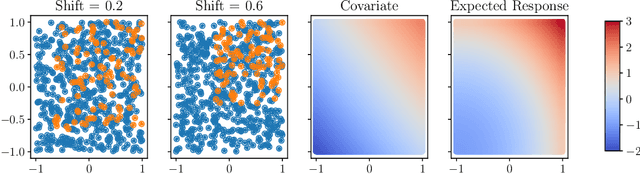
Linear models remain ubiquitous in modern spatial applications - including climate science, public health, and economics - due to their interpretability, speed, and reproducibility. While practitioners generally report a form of uncertainty, popular spatial uncertainty quantification methods do not jointly handle model misspecification and distribution shift - despite both being essentially always present in spatial problems. In the present paper, we show that existing methods for constructing confidence (or credible) intervals in spatial linear models fail to provide correct coverage due to unaccounted-for bias. In contrast to classical methods that rely on an i.i.d. assumption that is inappropriate in spatial problems, in the present work we instead make a spatial smoothness (Lipschitz) assumption. We are then able to propose a new confidence-interval construction that accounts for bias in the estimation procedure. We demonstrate that our new method achieves nominal coverage via both theory and experiments. Code to reproduce experiments is available at https://github.com/DavidRBurt/Lipschitz-Driven-Inference.

A Framework for Evaluating PM2.5 Forecasts from the Perspective of Individual Decision Making

Wildfire frequency is increasing as the climate changes, and the resulting air pollution poses health risks. Just as people routinely use weather forecasts to plan their activities around precipitation, reliable air quality forecasts could help individuals reduce their exposure to air pollution. In the present work, we evaluate several existing forecasts of fine particular matter (PM2.5) within the continental United States in the context of individual decision-making. Our comparison suggests there is meaningful room for improvement in air pollution forecasting, which might be realized by incorporating more data sources and using machine learning tools. To facilitate future machine learning development and benchmarking, we set up a framework to evaluate and compare air pollution forecasts for individual decision making. We introduce a new loss to capture decisions about when to use mitigation measures. We highlight the importance of visualizations when comparing forecasts. Finally, we provide code to download and compare archived forecast predictions.

Multi-marginal Schrödinger Bridges with Iterative Reference

Practitioners frequently aim to infer an unobserved population trajectory using sample snapshots at multiple time points. For instance, in single-cell sequencing, scientists would like to learn how gene expression evolves over time. But sequencing any cell destroys that cell. So we cannot access any cell's full trajectory, but we can access snapshot samples from many cells. Stochastic differential equations are commonly used to analyze systems with full individual-trajectory access; since here we have only sample snapshots, these methods are inapplicable. The deep learning community has recently explored using Schr\"odinger bridges (SBs) and their extensions to estimate these dynamics. However, these methods either (1) interpolate between just two time points or (2) require a single fixed reference dynamic within the SB, which is often just set to be Brownian motion. But learning piecewise from adjacent time points can fail to capture long-term dependencies. And practitioners are typically able to specify a model class for the reference dynamic but not the exact values of the parameters within it. So we propose a new method that (1) learns the unobserved trajectories from sample snapshots across multiple time points and (2) requires specification only of a class of reference dynamics, not a single fixed one. In particular, we suggest an iterative projection method inspired by Schr\"odinger bridges; we alternate between learning a piecewise SB on the unobserved trajectories and using the learned SB to refine our best guess for the dynamics within the reference class. We demonstrate the advantages of our method via a well-known simulated parametric model from ecology, simulated and real data from systems biology, and real motion-capture data.

Consistent Validation for Predictive Methods in Spatial Settings

Spatial prediction tasks are key to weather forecasting, studying air pollution, and other scientific endeavors. Determining how much to trust predictions made by statistical or physical methods is essential for the credibility of scientific conclusions. Unfortunately, classical approaches for validation fail to handle mismatch between locations available for validation and (test) locations where we want to make predictions. This mismatch is often not an instance of covariate shift (as commonly formalized) because the validation and test locations are fixed (e.g., on a grid or at select points) rather than i.i.d. from two distributions. In the present work, we formalize a check on validation methods: that they become arbitrarily accurate as validation data becomes arbitrarily dense. We show that classical and covariate-shift methods can fail this check. We instead propose a method that builds from existing ideas in the covariate-shift literature, but adapts them to the validation data at hand. We prove that our proposal passes our check. And we demonstrate its advantages empirically on simulated and real data.

Black Box Variational Inference with a Deterministic Objective: Faster, More Accurate, and Even More Black Box

Automatic differentiation variational inference (ADVI) offers fast and easy-to-use posterior approximation in multiple modern probabilistic programming languages. However, its stochastic optimizer lacks clear convergence criteria and requires tuning parameters. Moreover, ADVI inherits the poor posterior uncertainty estimates of mean-field variational Bayes (MFVB). We introduce ``deterministic ADVI'' (DADVI) to address these issues. DADVI replaces the intractable MFVB objective with a fixed Monte Carlo approximation, a technique known in the stochastic optimization literature as the ``sample average approximation'' (SAA). By optimizing an approximate but deterministic objective, DADVI can use off-the-shelf second-order optimization, and, unlike standard mean-field ADVI, is amenable to more accurate posterior linear response (LR) covariance estimates. In contrast to existing worst-case theory, we show that, on certain classes of common statistical problems, DADVI and the SAA can perform well with relatively few samples even in very high dimensions, though we also show that such favorable results cannot extend to variational approximations that are too expressive relative to mean-field ADVI. We show on a variety of real-world problems that DADVI reliably finds good solutions with default settings (unlike ADVI) and, together with LR covariances, is typically faster and more accurate than standard ADVI.

Gaussian processes at the Helm: A more fluid model for ocean currents

Oceanographers are interested in predicting ocean currents and identifying divergences in a current vector field based on sparse observations of buoy velocities. Since we expect current dynamics to be smooth but highly non-linear, Gaussian processes (GPs) offer an attractive model. But we show that applying a GP with a standard stationary kernel directly to buoy data can struggle at both current prediction and divergence identification -- due to some physically unrealistic prior assumptions. To better reflect known physical properties of currents, we propose to instead put a standard stationary kernel on the divergence and curl-free components of a vector field obtained through a Helmholtz decomposition. We show that, because this decomposition relates to the original vector field just via mixed partial derivatives, we can still perform inference given the original data with only a small constant multiple of additional computational expense. We illustrate the benefits of our method on synthetic and real ocean data.

Are you using test log-likelihood correctly?

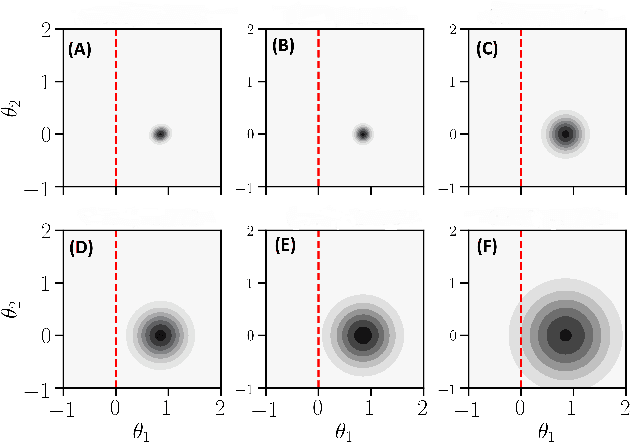
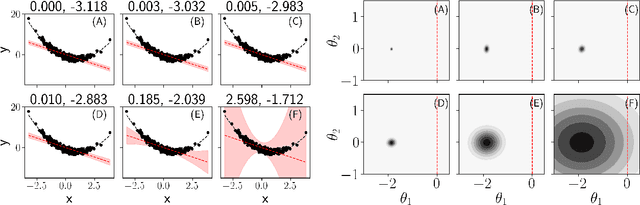
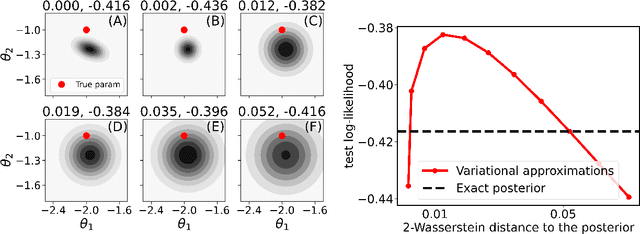
Test log-likelihood is commonly used to compare different models of the same data and different approximate inference algorithms for fitting the same probabilistic model. We present simple examples demonstrating how comparisons based on test log-likelihood can contradict comparisons according to other objectives. Specifically, our examples show that (i) conclusions about forecast accuracy based on test log-likelihood comparisons may not agree with conclusions based on other distributional quantities like means; and (ii) that approximate Bayesian inference algorithms that attain higher test log-likelihoods need not also yield more accurate posterior approximations.

Developing a Series of AI Challenges for the United States Department of the Air Force

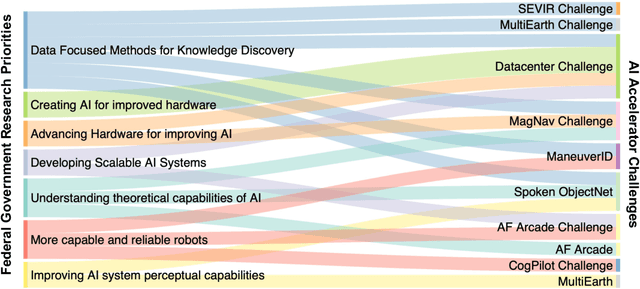
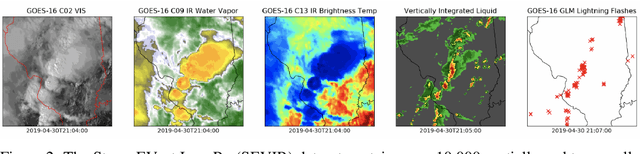
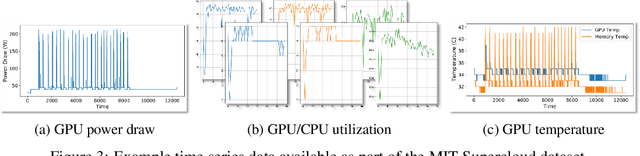
Through a series of federal initiatives and orders, the U.S. Government has been making a concerted effort to ensure American leadership in AI. These broad strategy documents have influenced organizations such as the United States Department of the Air Force (DAF). The DAF-MIT AI Accelerator is an initiative between the DAF and MIT to bridge the gap between AI researchers and DAF mission requirements. Several projects supported by the DAF-MIT AI Accelerator are developing public challenge problems that address numerous Federal AI research priorities. These challenges target priorities by making large, AI-ready datasets publicly available, incentivizing open-source solutions, and creating a demand signal for dual use technologies that can stimulate further research. In this article, we describe these public challenges being developed and how their application contributes to scientific advances.

Diffusion probabilistic modeling of protein backbones in 3D for the motif-scaffolding problem

Construction of a scaffold structure that supports a desired motif, conferring protein function, shows promise for the design of vaccines and enzymes. But a general solution to this motif-scaffolding problem remains open. Current machine-learning techniques for scaffold design are either limited to unrealistically small scaffolds (up to length 20) or struggle to produce multiple diverse scaffolds. We propose to learn a distribution over diverse and longer protein backbone structures via an E(3)-equivariant graph neural network. We develop SMCDiff to efficiently sample scaffolds from this distribution conditioned on a given motif; our algorithm is the first to theoretically guarantee conditional samples from a diffusion model in the large-compute limit. We evaluate our designed backbones by how well they align with AlphaFold2-predicted structures. We show that our method can (1) sample scaffolds up to 80 residues and (2) achieve structurally diverse scaffolds for a fixed motif.

Many processors, little time: MCMC for partitions via optimal transport couplings

Markov chain Monte Carlo (MCMC) methods are often used in clustering since they guarantee asymptotically exact expectations in the infinite-time limit. In finite time, though, slow mixing often leads to poor performance. Modern computing environments offer massive parallelism, but naive implementations of parallel MCMC can exhibit substantial bias. In MCMC samplers of continuous random variables, Markov chain couplings can overcome bias. But these approaches depend crucially on paired chains meetings after a small number of transitions. We show that straightforward applications of existing coupling ideas to discrete clustering variables fail to meet quickly. This failure arises from the "label-switching problem": semantically equivalent cluster relabelings impede fast meeting of coupled chains. We instead consider chains as exploring the space of partitions rather than partitions' (arbitrary) labelings. Using a metric on the partition space, we formulate a practical algorithm using optimal transport couplings. Our theory confirms our method is accurate and efficient. In experiments ranging from clustering of genes or seeds to graph colorings, we show the benefits of our coupling in the highly parallel, time-limited regime.