Consistent Validation for Predictive Methods in Spatial Settings
Paper and Code
Feb 05, 2024

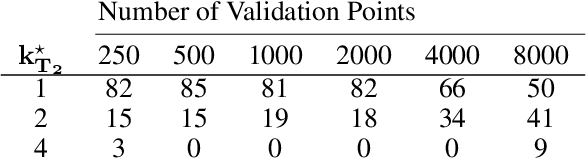

Spatial prediction tasks are key to weather forecasting, studying air pollution, and other scientific endeavors. Determining how much to trust predictions made by statistical or physical methods is essential for the credibility of scientific conclusions. Unfortunately, classical approaches for validation fail to handle mismatch between locations available for validation and (test) locations where we want to make predictions. This mismatch is often not an instance of covariate shift (as commonly formalized) because the validation and test locations are fixed (e.g., on a grid or at select points) rather than i.i.d. from two distributions. In the present work, we formalize a check on validation methods: that they become arbitrarily accurate as validation data becomes arbitrarily dense. We show that classical and covariate-shift methods can fail this check. We instead propose a method that builds from existing ideas in the covariate-shift literature, but adapts them to the validation data at hand. We prove that our proposal passes our check. And we demonstrate its advantages empirically on simulated and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge