OpenReview Should be Protected and Leveraged as a Community Asset for Research in the Era of Large Language Models

In the era of large language models (LLMs), high-quality, domain-rich, and continuously evolving datasets capturing expert-level knowledge, core human values, and reasoning are increasingly valuable. This position paper argues that OpenReview -- the continually evolving repository of research papers, peer reviews, author rebuttals, meta-reviews, and decision outcomes -- should be leveraged more broadly as a core community asset for advancing research in the era of LLMs. We highlight three promising areas in which OpenReview can uniquely contribute: enhancing the quality, scalability, and accountability of peer review processes; enabling meaningful, open-ended benchmarks rooted in genuine expert deliberation; and supporting alignment research through real-world interactions reflecting expert assessment, intentions, and scientific values. To better realize these opportunities, we suggest the community collaboratively explore standardized benchmarks and usage guidelines around OpenReview, inviting broader dialogue on responsible data use, ethical considerations, and collective stewardship.

Oh SnapMMD! Forecasting Stochastic Dynamics Beyond the Schrödinger Bridge's End

Scientists often want to make predictions beyond the observed time horizon of "snapshot" data following latent stochastic dynamics. For example, in time course single-cell mRNA profiling, scientists have access to cellular transcriptional state measurements (snapshots) from different biological replicates at different time points, but they cannot access the trajectory of any one cell because measurement destroys the cell. Researchers want to forecast (e.g.) differentiation outcomes from early state measurements of stem cells. Recent Schr\"odinger-bridge (SB) methods are natural for interpolating between snapshots. But past SB papers have not addressed forecasting -- likely since existing methods either (1) reduce to following pre-set reference dynamics (chosen before seeing data) or (2) require the user to choose a fixed, state-independent volatility since they minimize a Kullback-Leibler divergence. Either case can lead to poor forecasting quality. In the present work, we propose a new framework, SnapMMD, that learns dynamics by directly fitting the joint distribution of both state measurements and observation time with a maximum mean discrepancy (MMD) loss. Unlike past work, our method allows us to infer unknown and state-dependent volatilities from the observed data. We show in a variety of real and synthetic experiments that our method delivers accurate forecasts. Moreover, our approach allows us to learn in the presence of incomplete state measurements and yields an $R^2$-style statistic that diagnoses fit. We also find that our method's performance at interpolation (and general velocity-field reconstruction) is at least as good as (and often better than) state-of-the-art in almost all of our experiments.

Variational diffusion transformers for conditional sampling of supernovae spectra

Type Ia Supernovae (SNe Ia) have become the most precise distance indicators in astrophysics due to their incredible observational homogeneity. Increasing discovery rates, however, have revealed multiple sub-populations with spectroscopic properties that are both diverse and difficult to interpret using existing physical models. These peculiar events are hard to identify from sparsely sampled observations and can introduce systematics in cosmological analyses if not flagged early; they are also of broader importance for building a cohesive understanding of thermonuclear explosions. In this work, we introduce DiTSNe-Ia, a variational diffusion-based generative model conditioned on light curve observations and trained to reproduce the observed spectral diversity of SNe Ia. In experiments with realistic light curves and spectra from radiative transfer simulations, DiTSNe-Ia achieves significantly more accurate reconstructions than the widely used SALT3 templates across a broad range of observation phases (from 10 days before peak light to 30 days after it). DiTSNe-Ia yields a mean squared error of 0.108 across all phases-five times lower than SALT3's 0.508-and an after-peak error of just 0.0191, an order of magnitude smaller than SALT3's 0.305. Additionally, our model produces well-calibrated credible intervals with near-nominal coverage, particularly at post-peak phases. DiTSNe-Ia is a powerful tool for rapidly inferring the spectral properties of SNe Ia and other transient astrophysical phenomena for which a physical description does not yet exist.

Reviving The Classics: Active Reward Modeling in Large Language Model Alignment

Building neural reward models from human preferences is a pivotal component in reinforcement learning from human feedback (RLHF) and large language model alignment research. Given the scarcity and high cost of human annotation, how to select the most informative pairs to annotate is an essential yet challenging open problem. In this work, we highlight the insight that an ideal comparison dataset for reward modeling should balance exploration of the representation space and make informative comparisons between pairs with moderate reward differences. Technically, challenges arise in quantifying the two objectives and efficiently prioritizing the comparisons to be annotated. To address this, we propose the Fisher information-based selection strategies, adapt theories from the classical experimental design literature, and apply them to the final linear layer of the deep neural network-based reward modeling tasks. Empirically, our method demonstrates remarkable performance, high computational efficiency, and stability compared to other selection methods from deep learning and classical statistical literature across multiple open-source LLMs and datasets. Further ablation studies reveal that incorporating cross-prompt comparisons in active reward modeling significantly enhances labeling efficiency, shedding light on the potential for improved annotation strategies in RLHF.

Reusing Embeddings: Reproducible Reward Model Research in Large Language Model Alignment without GPUs

Large Language Models (LLMs) have made substantial strides in structured tasks through Reinforcement Learning (RL), demonstrating proficiency in mathematical reasoning and code generation. However, applying RL in broader domains like chatbots and content generation -- through the process known as Reinforcement Learning from Human Feedback (RLHF) -- presents unique challenges. Reward models in RLHF are critical, acting as proxies that evaluate the alignment of LLM outputs with human intent. Despite advancements, the development of reward models is hindered by challenges such as computational heavy training, costly evaluation, and therefore poor reproducibility. We advocate for using embedding-based input in reward model research as an accelerated solution to those challenges. By leveraging embeddings for reward modeling, we can enhance reproducibility, reduce computational demands on hardware, improve training stability, and significantly reduce training and evaluation costs, hence facilitating fair and efficient comparisons in this active research area. We then show a case study of reproducing existing reward model ensemble research using embedding-based reward models. We discussed future avenues for research, aiming to contribute to safer and more effective LLM deployments.

Rethinking Bradley-Terry Models in Preference-Based Reward Modeling: Foundations, Theory, and Alternatives

The Bradley-Terry (BT) model is a common and successful practice in reward modeling for Large Language Model (LLM) alignment. However, it remains unclear why this model -- originally developed for multi-player stochastic game matching -- can be adopted to convert pairwise response comparisons to reward values and make predictions. Especially given the fact that only a limited number of prompt-response pairs are sparsely compared with others. In this paper, we first revisit the foundations of using BT models in reward modeling, and establish the convergence rate of BT reward models based on deep neural networks using embeddings, providing a theoretical foundation for their use. Despite theoretically sound, we argue that the BT model is not a necessary choice from the perspective of downstream optimization. This is because a reward model only needs to preserve the correct ranking predictions through a monotonic transformation of the true reward. We highlight the critical concept of order consistency in reward modeling and demonstrate that the BT model possesses this property. Consequently, we propose a simple and straightforward upper-bound algorithm, compatible with off-the-shelf binary classifiers, as an alternative order-consistent reward modeling objective. To offer practical insights, we empirically evaluate the performance of these different reward modeling approaches across more than 12,000 experimental setups, using $6$ base LLMs, $2$ datasets, and diverse annotation designs that vary in quantity, quality, and pairing choices in preference annotations.

Multi-marginal Schrödinger Bridges with Iterative Reference

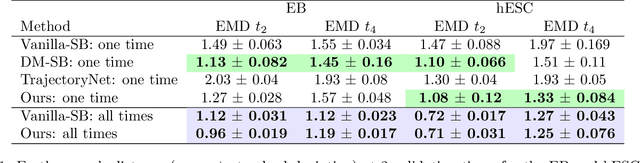
Practitioners frequently aim to infer an unobserved population trajectory using sample snapshots at multiple time points. For instance, in single-cell sequencing, scientists would like to learn how gene expression evolves over time. But sequencing any cell destroys that cell. So we cannot access any cell's full trajectory, but we can access snapshot samples from many cells. Stochastic differential equations are commonly used to analyze systems with full individual-trajectory access; since here we have only sample snapshots, these methods are inapplicable. The deep learning community has recently explored using Schr\"odinger bridges (SBs) and their extensions to estimate these dynamics. However, these methods either (1) interpolate between just two time points or (2) require a single fixed reference dynamic within the SB, which is often just set to be Brownian motion. But learning piecewise from adjacent time points can fail to capture long-term dependencies. And practitioners are typically able to specify a model class for the reference dynamic but not the exact values of the parameters within it. So we propose a new method that (1) learns the unobserved trajectories from sample snapshots across multiple time points and (2) requires specification only of a class of reference dynamics, not a single fixed one. In particular, we suggest an iterative projection method inspired by Schr\"odinger bridges; we alternate between learning a piecewise SB on the unobserved trajectories and using the learned SB to refine our best guess for the dynamics within the reference class. We demonstrate the advantages of our method via a well-known simulated parametric model from ecology, simulated and real data from systems biology, and real motion-capture data.

Consistent Validation for Predictive Methods in Spatial Settings

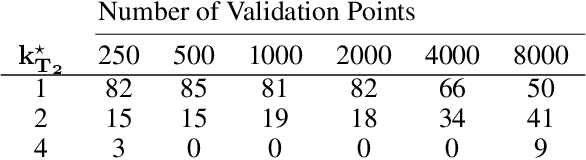
Spatial prediction tasks are key to weather forecasting, studying air pollution, and other scientific endeavors. Determining how much to trust predictions made by statistical or physical methods is essential for the credibility of scientific conclusions. Unfortunately, classical approaches for validation fail to handle mismatch between locations available for validation and (test) locations where we want to make predictions. This mismatch is often not an instance of covariate shift (as commonly formalized) because the validation and test locations are fixed (e.g., on a grid or at select points) rather than i.i.d. from two distributions. In the present work, we formalize a check on validation methods: that they become arbitrarily accurate as validation data becomes arbitrarily dense. We show that classical and covariate-shift methods can fail this check. We instead propose a method that builds from existing ideas in the covariate-shift literature, but adapts them to the validation data at hand. We prove that our proposal passes our check. And we demonstrate its advantages empirically on simulated and real data.