Black Box Variational Inference with a Deterministic Objective: Faster, More Accurate, and Even More Black Box

Automatic differentiation variational inference (ADVI) offers fast and easy-to-use posterior approximation in multiple modern probabilistic programming languages. However, its stochastic optimizer lacks clear convergence criteria and requires tuning parameters. Moreover, ADVI inherits the poor posterior uncertainty estimates of mean-field variational Bayes (MFVB). We introduce ``deterministic ADVI'' (DADVI) to address these issues. DADVI replaces the intractable MFVB objective with a fixed Monte Carlo approximation, a technique known in the stochastic optimization literature as the ``sample average approximation'' (SAA). By optimizing an approximate but deterministic objective, DADVI can use off-the-shelf second-order optimization, and, unlike standard mean-field ADVI, is amenable to more accurate posterior linear response (LR) covariance estimates. In contrast to existing worst-case theory, we show that, on certain classes of common statistical problems, DADVI and the SAA can perform well with relatively few samples even in very high dimensions, though we also show that such favorable results cannot extend to variational approximations that are too expressive relative to mean-field ADVI. We show on a variety of real-world problems that DADVI reliably finds good solutions with default settings (unlike ADVI) and, together with LR covariances, is typically faster and more accurate than standard ADVI.

Gaussian processes at the Helm: A more fluid model for ocean currents

Oceanographers are interested in predicting ocean currents and identifying divergences in a current vector field based on sparse observations of buoy velocities. Since we expect current dynamics to be smooth but highly non-linear, Gaussian processes (GPs) offer an attractive model. But we show that applying a GP with a standard stationary kernel directly to buoy data can struggle at both current prediction and divergence identification -- due to some physically unrealistic prior assumptions. To better reflect known physical properties of currents, we propose to instead put a standard stationary kernel on the divergence and curl-free components of a vector field obtained through a Helmholtz decomposition. We show that, because this decomposition relates to the original vector field just via mixed partial derivatives, we can still perform inference given the original data with only a small constant multiple of additional computational expense. We illustrate the benefits of our method on synthetic and real ocean data.

Evaluating Sensitivity to the Stick-Breaking Prior in Bayesian Nonparametrics

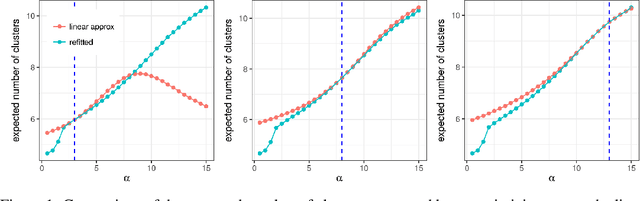
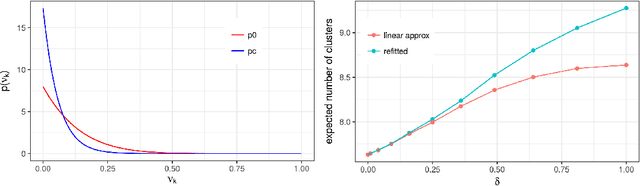
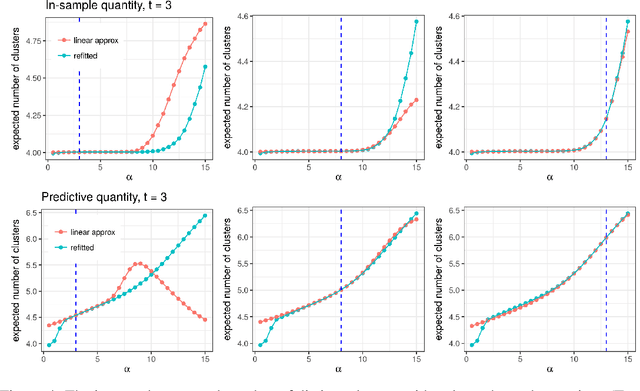
Bayesian models based on the Dirichlet process and other stick-breaking priors have been proposed as core ingredients for clustering, topic modeling, and other unsupervised learning tasks. Prior specification is, however, relatively difficult for such models, given that their flexibility implies that the consequences of prior choices are often relatively opaque. Moreover, these choices can have a substantial effect on posterior inferences. Thus, considerations of robustness need to go hand in hand with nonparametric modeling. In the current paper, we tackle this challenge by exploiting the fact that variational Bayesian methods, in addition to having computational advantages in fitting complex nonparametric models, also yield sensitivities with respect to parametric and nonparametric aspects of Bayesian models. In particular, we demonstrate how to assess the sensitivity of conclusions to the choice of concentration parameter and stick-breaking distribution for inferences under Dirichlet process mixtures and related mixture models. We provide both theoretical and empirical support for our variational approach to Bayesian sensitivity analysis.

A Higher-Order Swiss Army Infinitesimal Jackknife

Cross validation (CV) and the bootstrap are ubiquitous model-agnostic tools for assessing the error or variability of machine learning and statistical estimators. However, these methods require repeatedly re-fitting the model with different weighted versions of the original dataset, which can be prohibitively time-consuming. For sufficiently regular optimization problems the optimum depends smoothly on the data weights, and so the process of repeatedly re-fitting can be approximated with a Taylor series that can be often evaluated relatively quickly. The first-order approximation is known as the "infinitesimal jackknife" in the statistics literature and has been the subject of recent interest in machine learning for approximate CV. In this work, we consider high-order approximations, which we call the "higher-order infinitesimal jackknife" (HOIJ). Under mild regularity conditions, we provide a simple recursive procedure to compute approximations of all orders with finite-sample accuracy bounds. Additionally, we show that the HOIJ can be efficiently computed even in high dimensions using forward-mode automatic differentiation. We show that a linear approximation with bootstrap weights approximation is equivalent to those provided by asymptotic normal approximations. Consequently, the HOIJ opens up the possibility of enjoying higher-order accuracy properties of the bootstrap using local approximations. Consistency of the HOIJ for leave-one-out CV under different asymptotic regimes follows as corollaries from our finite-sample bounds under additional regularity assumptions. The generality of the computation and bounds motivate the name "higher-order Swiss Army infinitesimal jackknife."

Learning an Astronomical Catalog of the Visible Universe through Scalable Bayesian Inference

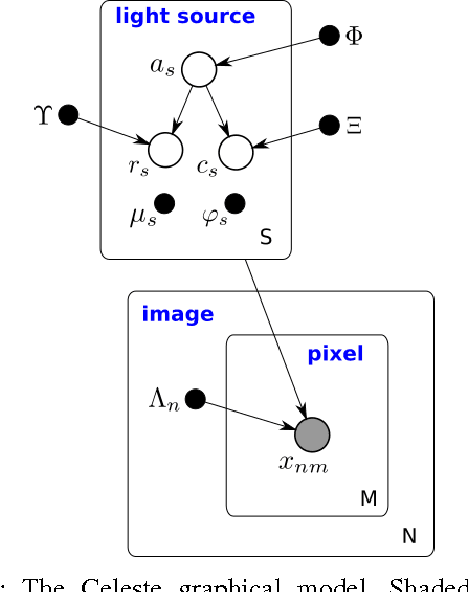
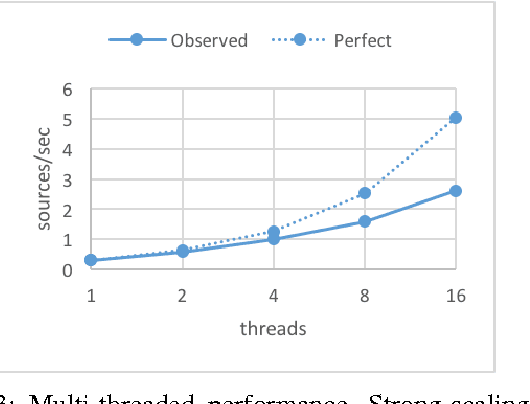
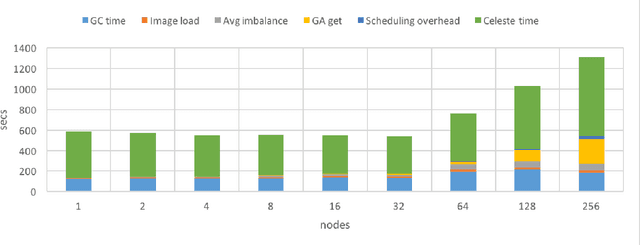
Celeste is a procedure for inferring astronomical catalogs that attains state-of-the-art scientific results. To date, Celeste has been scaled to at most hundreds of megabytes of astronomical images: Bayesian posterior inference is notoriously demanding computationally. In this paper, we report on a scalable, parallel version of Celeste, suitable for learning catalogs from modern large-scale astronomical datasets. Our algorithmic innovations include a fast numerical optimization routine for Bayesian posterior inference and a statistically efficient scheme for decomposing astronomical optimization problems into subproblems. Our scalable implementation is written entirely in Julia, a new high-level dynamic programming language designed for scientific and numerical computing. We use Julia's high-level constructs for shared and distributed memory parallelism, and demonstrate effective load balancing and efficient scaling on up to 8192 Xeon cores on the NERSC Cori supercomputer.

Fast robustness quantification with variational Bayes

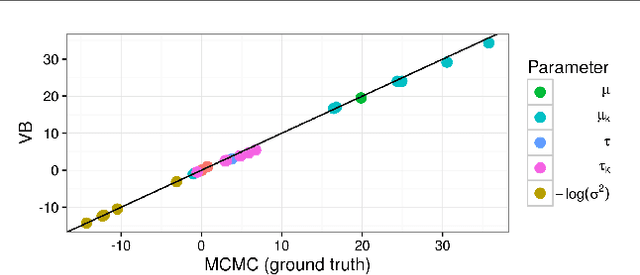
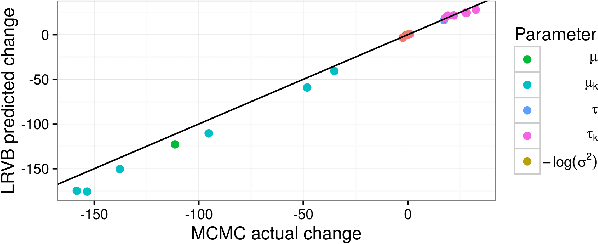
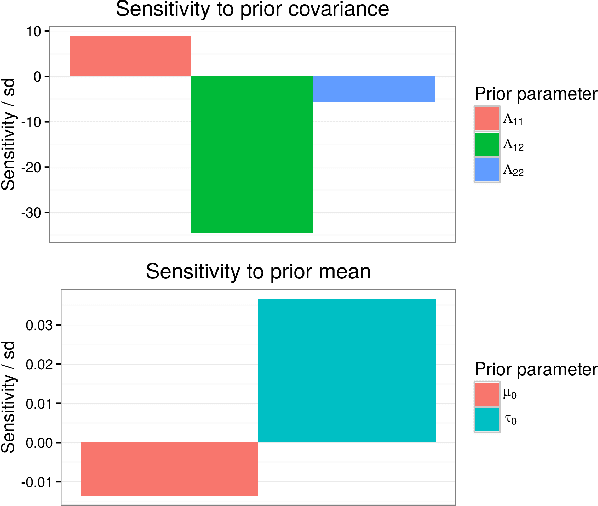
Bayesian hierarchical models are increasing popular in economics. When using hierarchical models, it is useful not only to calculate posterior expectations, but also to measure the robustness of these expectations to reasonable alternative prior choices. We use variational Bayes and linear response methods to provide fast, accurate posterior means and robustness measures with an application to measuring the effectiveness of microcredit in the developing world.

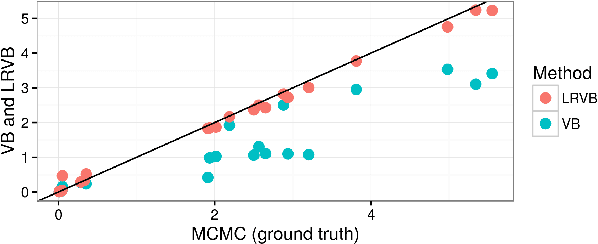
Linear Response Methods for Accurate Covariance Estimates from Mean Field Variational Bayes

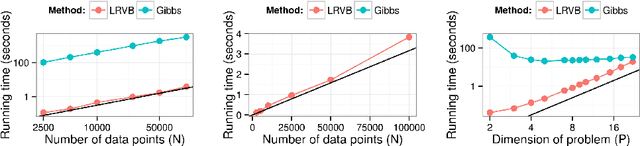
Mean field variational Bayes (MFVB) is a popular posterior approximation method due to its fast runtime on large-scale data sets. However, it is well known that a major failing of MFVB is that it underestimates the uncertainty of model variables (sometimes severely) and provides no information about model variable covariance. We generalize linear response methods from statistical physics to deliver accurate uncertainty estimates for model variables---both for individual variables and coherently across variables. We call our method linear response variational Bayes (LRVB). When the MFVB posterior approximation is in the exponential family, LRVB has a simple, analytic form, even for non-conjugate models. Indeed, we make no assumptions about the form of the true posterior. We demonstrate the accuracy and scalability of our method on a range of models for both simulated and real data.

Covariance Matrices and Influence Scores for Mean Field Variational Bayes

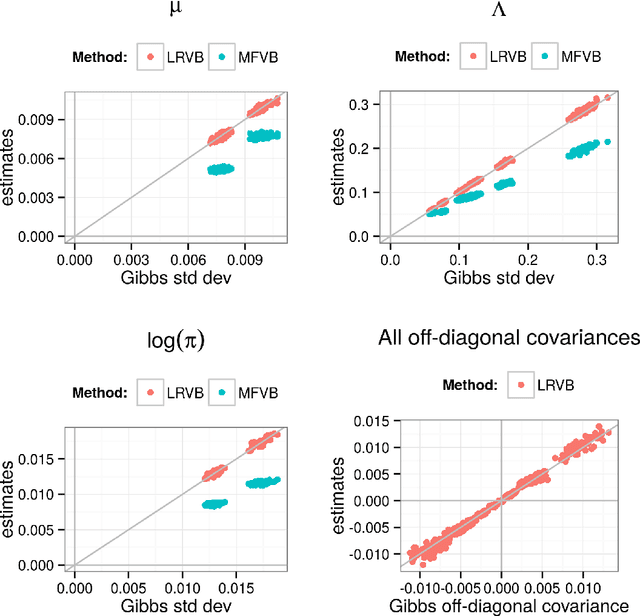
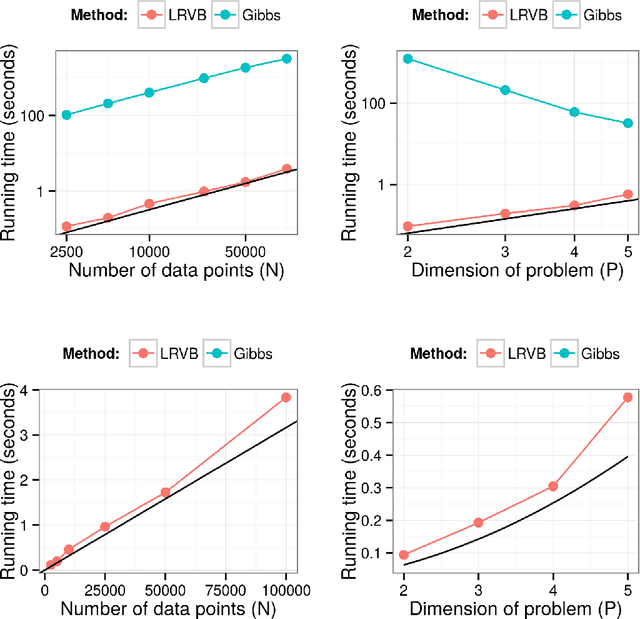
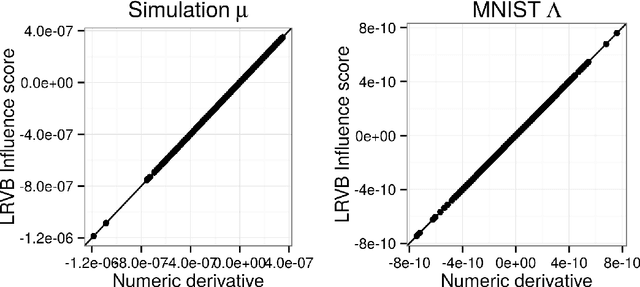
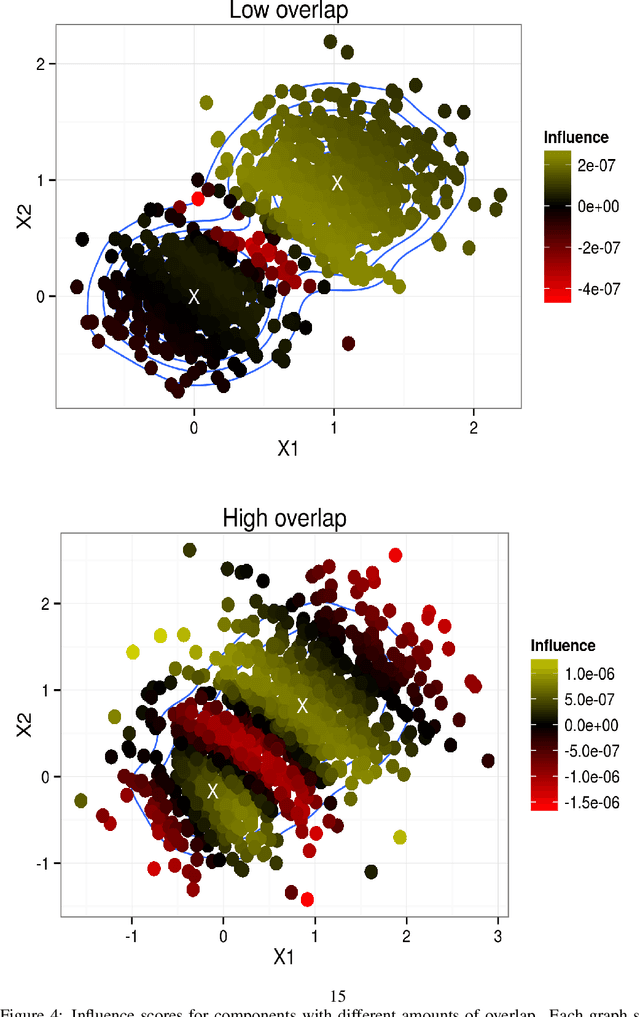
Mean field variational Bayes (MFVB) is a popular posterior approximation method due to its fast runtime on large-scale data sets. However, it is well known that a major failing of MFVB is that it underestimates the uncertainty of model variables (sometimes severely) and provides no information about model variable covariance. We develop a fast, general methodology for exponential families that augments MFVB to deliver accurate uncertainty estimates for model variables -- both for individual variables and coherently across variables. MFVB for exponential families defines a fixed-point equation in the means of the approximating posterior, and our approach yields a covariance estimate by perturbing this fixed point. Inspired by linear response theory, we call our method linear response variational Bayes (LRVB). We also show how LRVB can be used to quickly calculate a measure of the influence of individual data points on parameter point estimates. We demonstrate the accuracy and scalability of our method by learning Gaussian mixture models for both simulated and real data.

Covariance Matrices for Mean Field Variational Bayes

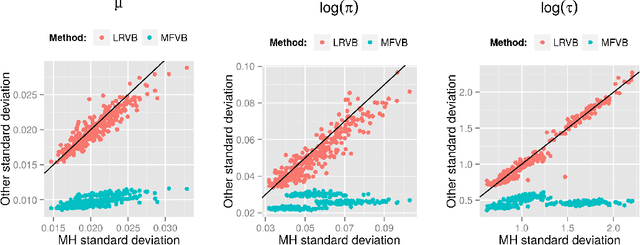
Mean Field Variational Bayes (MFVB) is a popular posterior approximation method due to its fast runtime on large-scale data sets. However, it is well known that a major failing of MFVB is its (sometimes severe) underestimates of the uncertainty of model variables and lack of information about model variable covariance. We develop a fast, general methodology for exponential families that augments MFVB to deliver accurate uncertainty estimates for model variables -- both for individual variables and coherently across variables. MFVB for exponential families defines a fixed-point equation in the means of the approximating posterior, and our approach yields a covariance estimate by perturbing this fixed point. Inspired by linear response theory, we call our method linear response variational Bayes (LRVB). We demonstrate the accuracy of our method on simulated data sets.