Jon McAuliffe
Rao-Blackwellized Stochastic Gradients for Discrete Distributions
Oct 10, 2018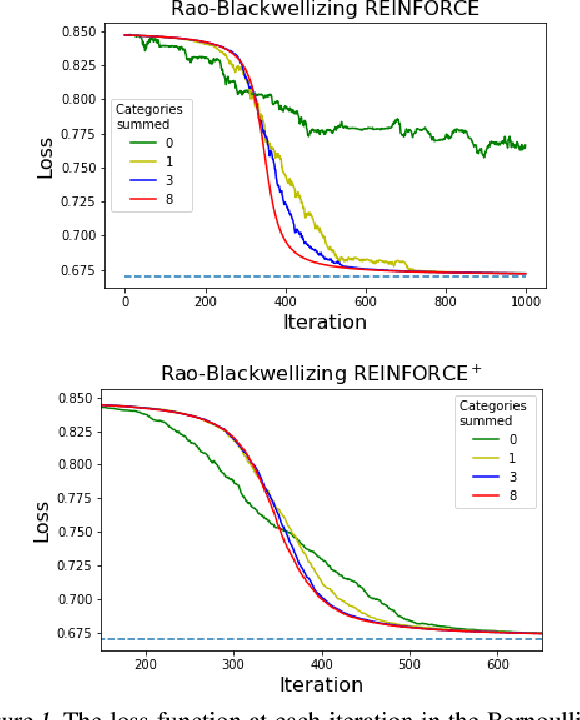
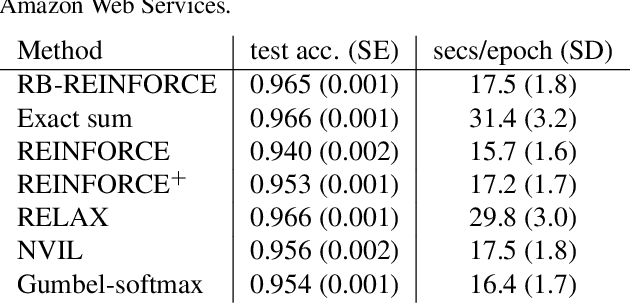
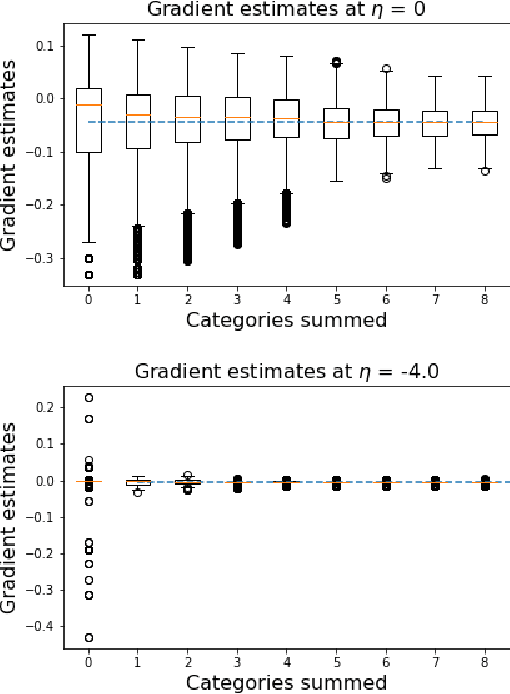
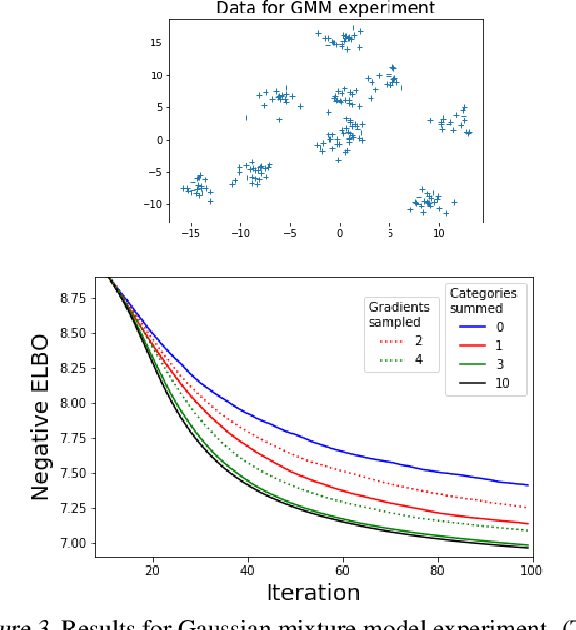
Abstract:We wish to compute the gradient of an expectation over a finite or countably infinite sample space having $K \leq \infty$ categories. When $K$ is indeed infinite, or finite but very large, the relevant summation is intractable. Accordingly, various stochastic gradient estimators have been proposed. In this paper, we describe a technique that can be applied to reduce the variance of any such estimator, without changing its bias---in particular, unbiasedness is retained. We show that our technique is an instance of Rao-Blackwellization, and we demonstrate the improvement it yields in empirical studies on both synthetic and real-world data.
Fast Black-box Variational Inference through Stochastic Trust-Region Optimization
Nov 05, 2017
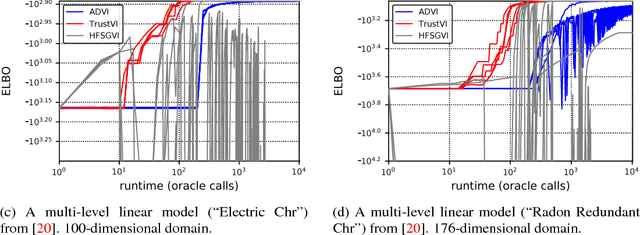
Abstract:We introduce TrustVI, a fast second-order algorithm for black-box variational inference based on trust-region optimization and the reparameterization trick. At each iteration, TrustVI proposes and assesses a step based on minibatches of draws from the variational distribution. The algorithm provably converges to a stationary point. We implemented TrustVI in the Stan framework and compared it to two alternatives: Automatic Differentiation Variational Inference (ADVI) and Hessian-free Stochastic Gradient Variational Inference (HFSGVI). The former is based on stochastic first-order optimization. The latter uses second-order information, but lacks convergence guarantees. TrustVI typically converged at least one order of magnitude faster than ADVI, demonstrating the value of stochastic second-order information. TrustVI often found substantially better variational distributions than HFSGVI, demonstrating that our convergence theory can matter in practice.
Learning an Astronomical Catalog of the Visible Universe through Scalable Bayesian Inference
Nov 10, 2016
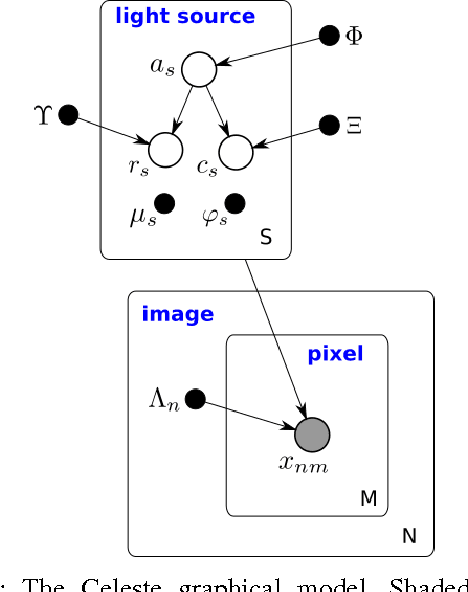
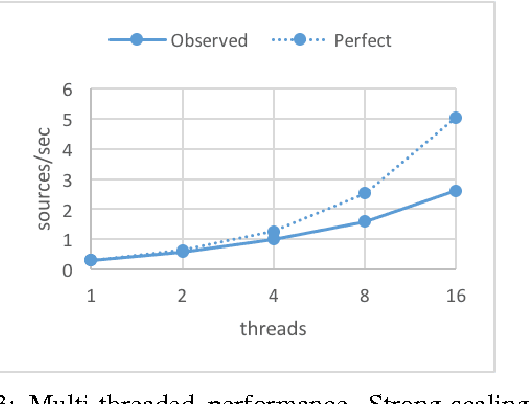
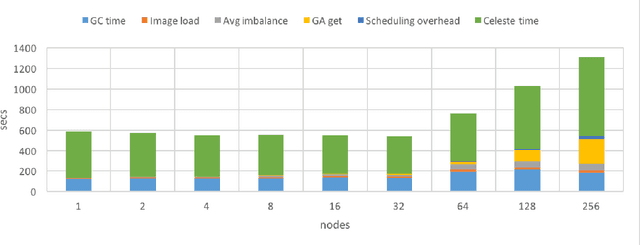
Abstract:Celeste is a procedure for inferring astronomical catalogs that attains state-of-the-art scientific results. To date, Celeste has been scaled to at most hundreds of megabytes of astronomical images: Bayesian posterior inference is notoriously demanding computationally. In this paper, we report on a scalable, parallel version of Celeste, suitable for learning catalogs from modern large-scale astronomical datasets. Our algorithmic innovations include a fast numerical optimization routine for Bayesian posterior inference and a statistically efficient scheme for decomposing astronomical optimization problems into subproblems. Our scalable implementation is written entirely in Julia, a new high-level dynamic programming language designed for scientific and numerical computing. We use Julia's high-level constructs for shared and distributed memory parallelism, and demonstrate effective load balancing and efficient scaling on up to 8192 Xeon cores on the NERSC Cori supercomputer.
Celeste: Variational inference for a generative model of astronomical images
Jun 03, 2015
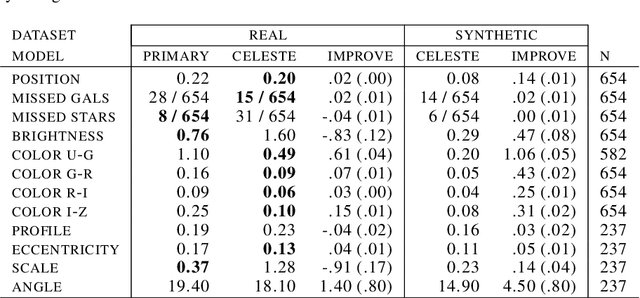
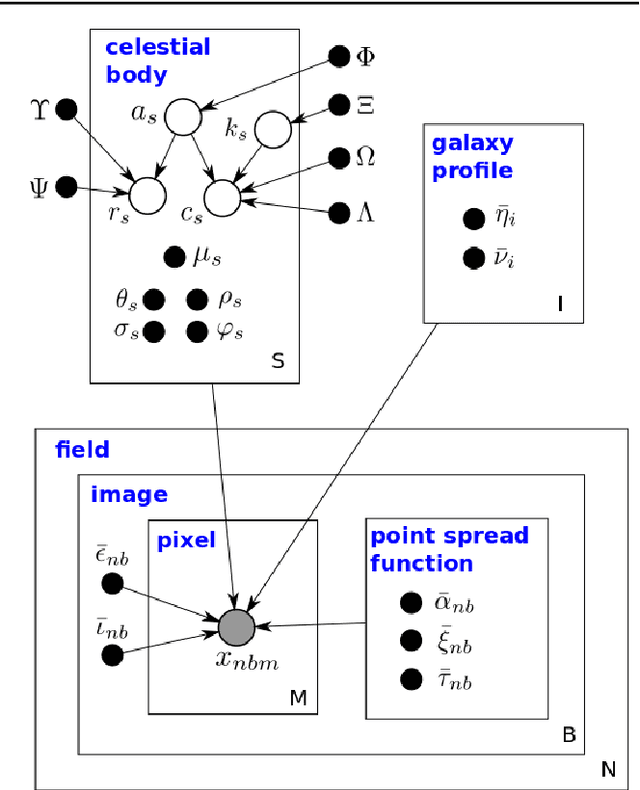
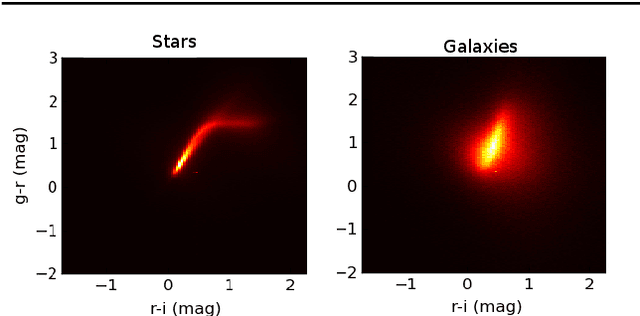
Abstract:We present a new, fully generative model of optical telescope image sets, along with a variational procedure for inference. Each pixel intensity is treated as a Poisson random variable, with a rate parameter dependent on latent properties of stars and galaxies. Key latent properties are themselves random, with scientific prior distributions constructed from large ancillary data sets. We check our approach on synthetic images. We also run it on images from a major sky survey, where it exceeds the performance of the current state-of-the-art method for locating celestial bodies and measuring their colors.
Variational inference for large-scale models of discrete choice
Jan 15, 2008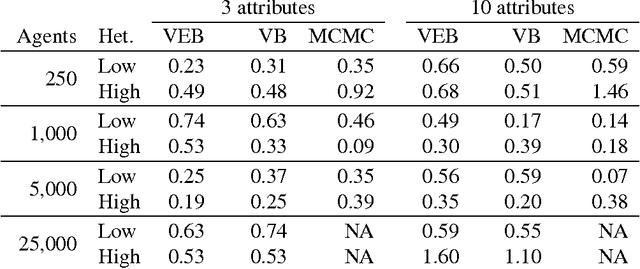
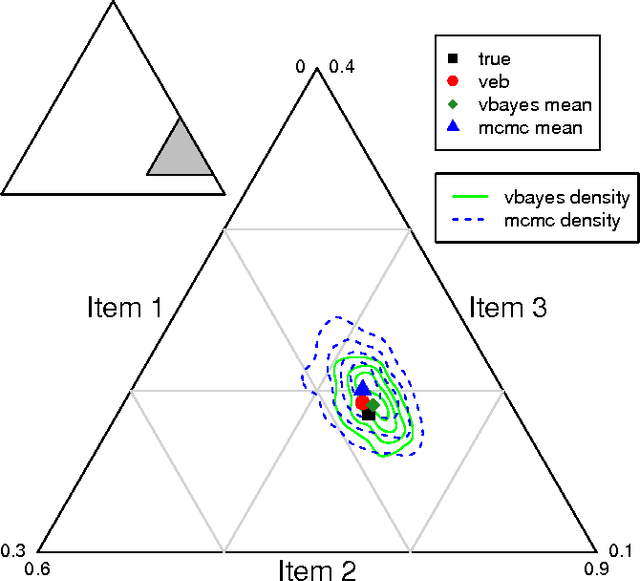
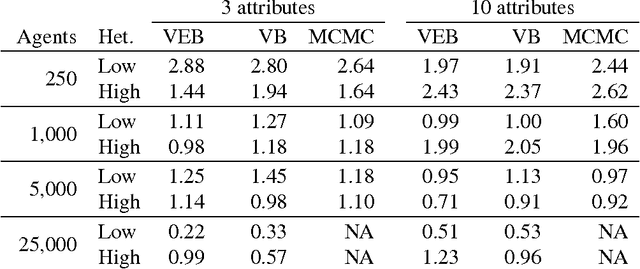
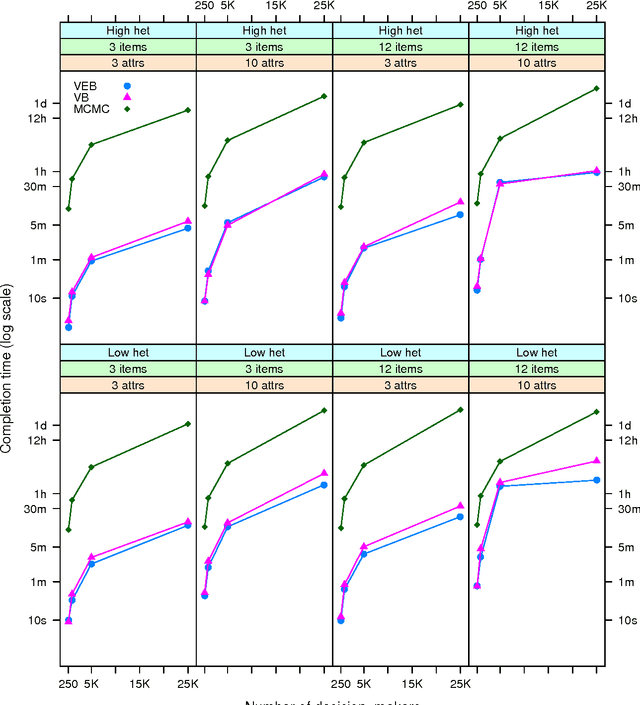
Abstract:Discrete choice models are commonly used by applied statisticians in numerous fields, such as marketing, economics, finance, and operations research. When agents in discrete choice models are assumed to have differing preferences, exact inference is often intractable. Markov chain Monte Carlo techniques make approximate inference possible, but the computational cost is prohibitive on the large data sets now becoming routinely available. Variational methods provide a deterministic alternative for approximation of the posterior distribution. We derive variational procedures for empirical Bayes and fully Bayesian inference in the mixed multinomial logit model of discrete choice. The algorithms require only that we solve a sequence of unconstrained optimization problems, which are shown to be convex. Extensive simulations demonstrate that variational methods achieve accuracy competitive with Markov chain Monte Carlo, at a small fraction of the computational cost. Thus, variational methods permit inferences on data sets that otherwise could not be analyzed without bias-inducing modifications to the underlying model.
* 29 pages, 2 tables, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge