SiamReID: Confuser Aware Siamese Tracker with Re-identification Feature

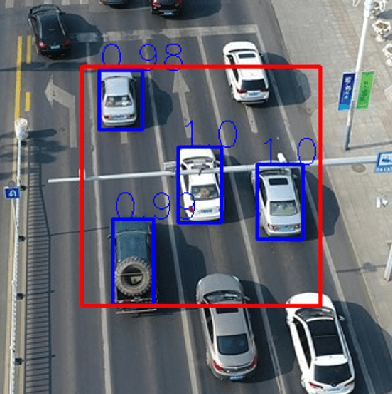
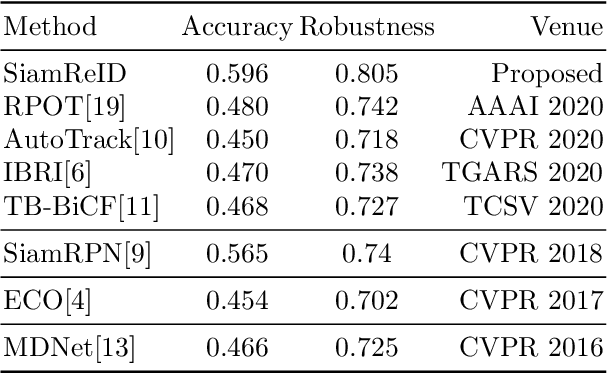
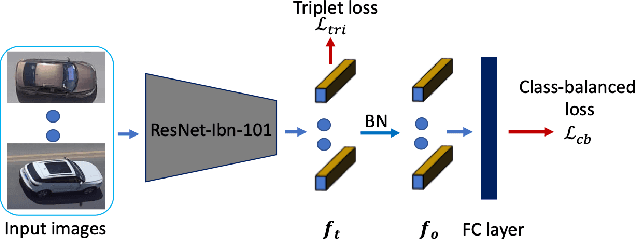
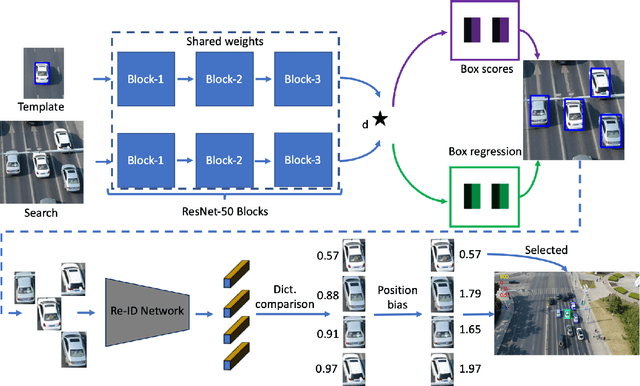
Siamese deep-network trackers have received significant attention in recent years due to their real-time speed and state-of-the-art performance. However, Siamese trackers suffer from similar looking confusers, that are prevalent in aerial imagery and create challenging conditions due to prolonged occlusions where the tracker object re-appears under different pose and illumination. Our work proposes SiamReID, a novel re-identification framework for Siamese trackers, that incorporates confuser rejection during prolonged occlusions and is well-suited for aerial tracking. The re-identification feature is trained using both triplet loss and a class balanced loss. Our approach achieves state-of-the-art performance in the UAVDT single object tracking benchmark.

Local Gathering of Mobile Robots in Three Dimensions

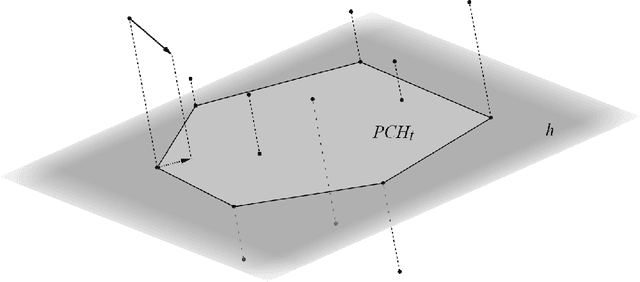
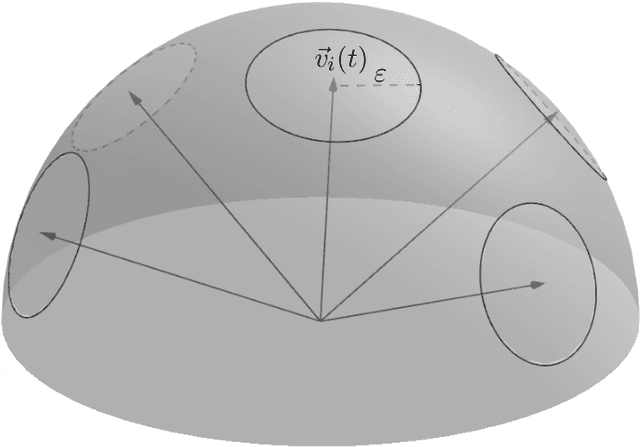
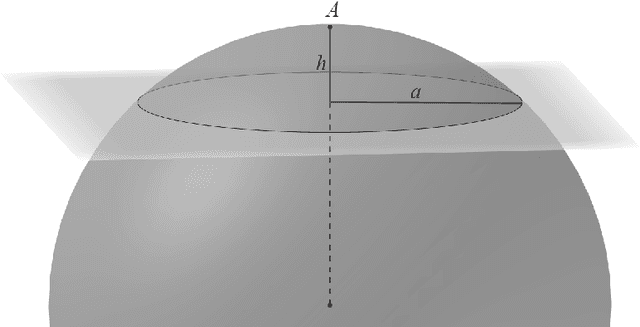
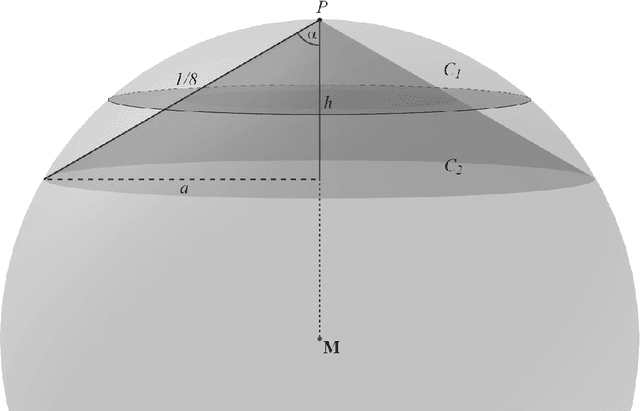
In this work, we initiate the research about the Gathering problem for robots with limited viewing range in the three-dimensional Euclidean space. In the Gathering problem, a set of initially scattered robots is required to gather at the same position. The robots' capabilities are very restricted -- they do not agree on any coordinate system or compass, have a limited viewing range, have no memory of the past and cannot communicate. We study the problem in two different time models, in FSYNC (fully synchronized discrete rounds) and the continuous time model. For FSYNC, we introduce the 3D-Go-To-The-Center-strategy and prove a runtime of $\Theta(n^2)$ that matches the currently best runtime bound for the same model in the Euclidean plane [SPAA'11]. Our main result is the generalization of contracting strategies (continuous time) from [Algosensors'17] to three dimensions. In contracting strategies, every robot that is located on the global convex hull of all robots' positions moves with full speed towards the inside of the convex hull. We prove a runtime bound of $O(\Delta \cdot n^{3/2})$ for any three-dimensional contracting strategy, where $\Delta$ denotes the diameter of the initial configuration. This comes up to a factor of $\sqrt{n}$ close to the lower bound of $\Omega (\Delta \cdot n)$ which is already true in two dimensions. In general, it might be hard for robots with limited viewing range to decide whether they are located on the global convex hull and which movement maintains the connectivity of the swarm, rendering the design of concrete contracting strategies a challenging task. We prove that the continuous variant of 3D-Go-To-The-Center is contracting and keeps the swarm connected. Moreover, we give a simple design criterion for three-dimensional contracting strategies that maintains the connectivity of the swarm and introduce an exemplary strategy based on this criterion.

Variational inference for large-scale models of discrete choice

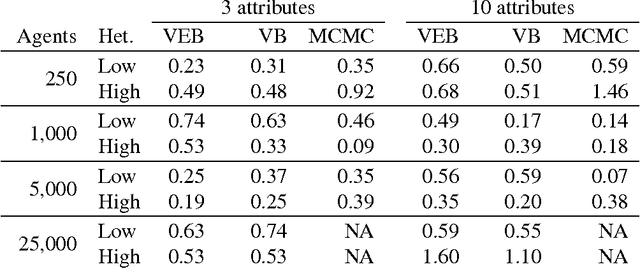
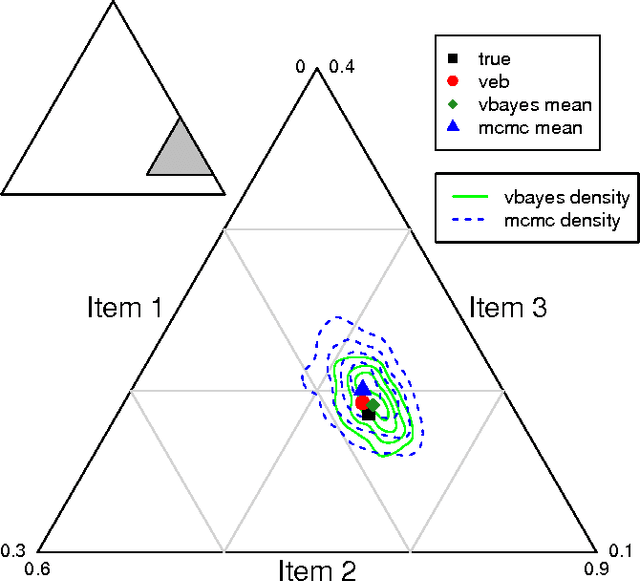
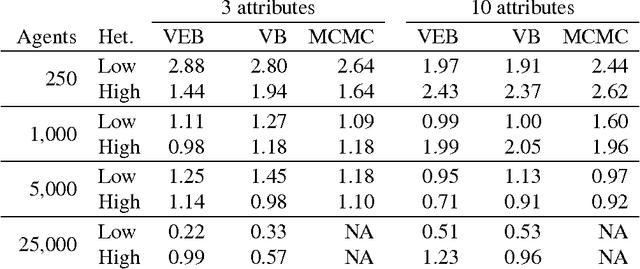
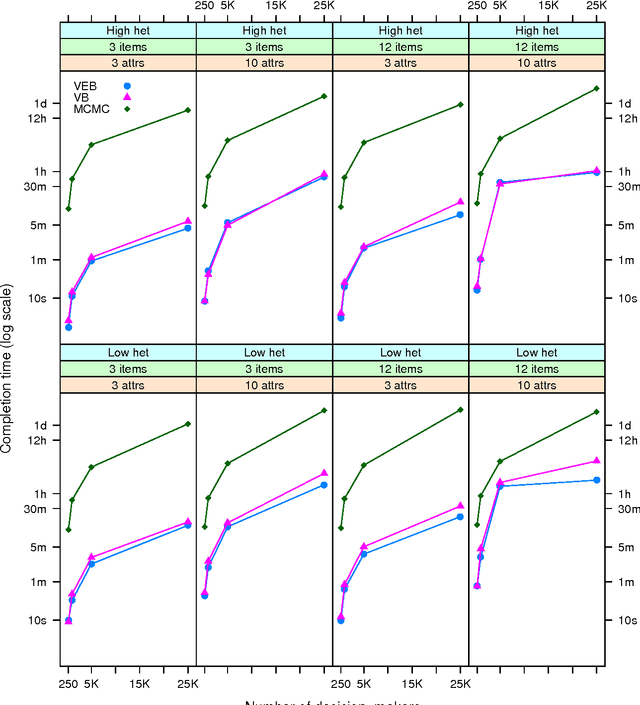
Discrete choice models are commonly used by applied statisticians in numerous fields, such as marketing, economics, finance, and operations research. When agents in discrete choice models are assumed to have differing preferences, exact inference is often intractable. Markov chain Monte Carlo techniques make approximate inference possible, but the computational cost is prohibitive on the large data sets now becoming routinely available. Variational methods provide a deterministic alternative for approximation of the posterior distribution. We derive variational procedures for empirical Bayes and fully Bayesian inference in the mixed multinomial logit model of discrete choice. The algorithms require only that we solve a sequence of unconstrained optimization problems, which are shown to be convex. Extensive simulations demonstrate that variational methods achieve accuracy competitive with Markov chain Monte Carlo, at a small fraction of the computational cost. Thus, variational methods permit inferences on data sets that otherwise could not be analyzed without bias-inducing modifications to the underlying model.