Local Gathering of Mobile Robots in Three Dimensions

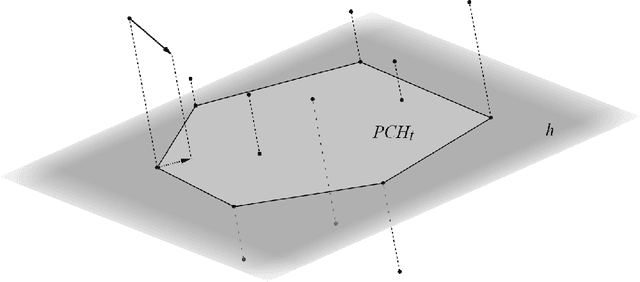
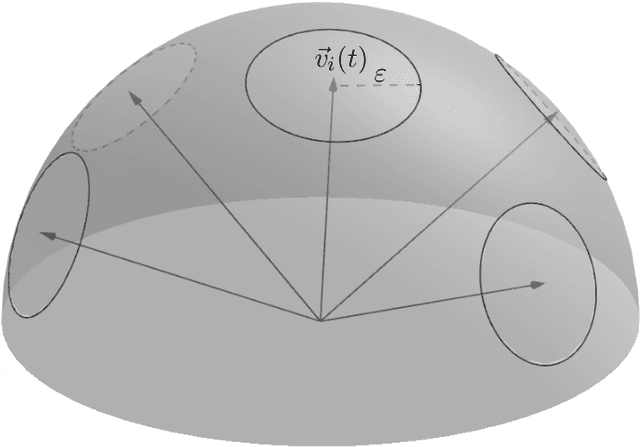
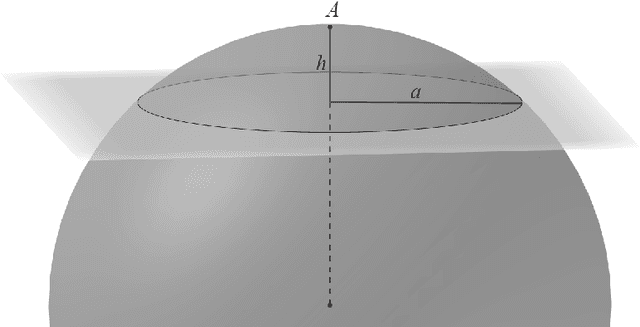
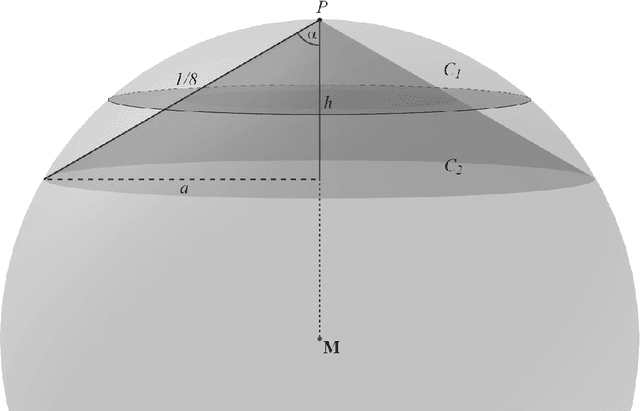
In this work, we initiate the research about the Gathering problem for robots with limited viewing range in the three-dimensional Euclidean space. In the Gathering problem, a set of initially scattered robots is required to gather at the same position. The robots' capabilities are very restricted -- they do not agree on any coordinate system or compass, have a limited viewing range, have no memory of the past and cannot communicate. We study the problem in two different time models, in FSYNC (fully synchronized discrete rounds) and the continuous time model. For FSYNC, we introduce the 3D-Go-To-The-Center-strategy and prove a runtime of $\Theta(n^2)$ that matches the currently best runtime bound for the same model in the Euclidean plane [SPAA'11]. Our main result is the generalization of contracting strategies (continuous time) from [Algosensors'17] to three dimensions. In contracting strategies, every robot that is located on the global convex hull of all robots' positions moves with full speed towards the inside of the convex hull. We prove a runtime bound of $O(\Delta \cdot n^{3/2})$ for any three-dimensional contracting strategy, where $\Delta$ denotes the diameter of the initial configuration. This comes up to a factor of $\sqrt{n}$ close to the lower bound of $\Omega (\Delta \cdot n)$ which is already true in two dimensions. In general, it might be hard for robots with limited viewing range to decide whether they are located on the global convex hull and which movement maintains the connectivity of the swarm, rendering the design of concrete contracting strategies a challenging task. We prove that the continuous variant of 3D-Go-To-The-Center is contracting and keeps the swarm connected. Moreover, we give a simple design criterion for three-dimensional contracting strategies that maintains the connectivity of the swarm and introduce an exemplary strategy based on this criterion.

Gathering Anonymous, Oblivious Robots on a Grid

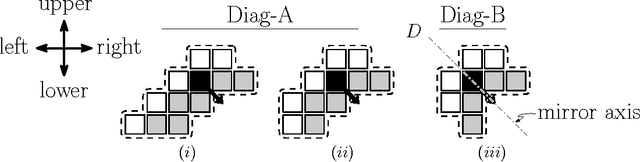
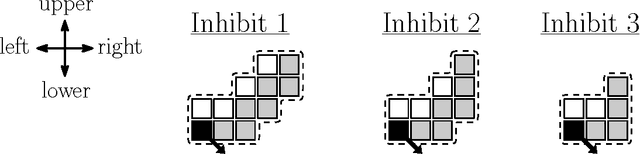
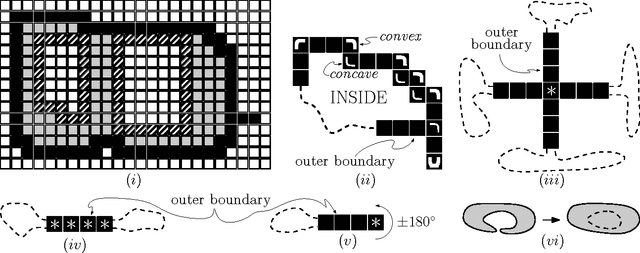
We consider a swarm of $n$ autonomous mobile robots, distributed on a 2-dimensional grid. A basic task for such a swarm is the gathering process: All robots have to gather at one (not predefined) place. A common local model for extremely simple robots is the following: The robots do not have a common compass, only have a constant viewing radius, are autonomous and indistinguishable, can move at most a constant distance in each step, cannot communicate, are oblivious and do not have flags or states. The only gathering algorithm under this robot model, with known runtime bounds, needs $\mathcal{O}(n^2)$ rounds and works in the Euclidean plane. The underlying time model for the algorithm is the fully synchronous $\mathcal{FSYNC}$ model. On the other side, in the case of the 2-dimensional grid, the only known gathering algorithms for the same time and a similar local model additionally require a constant memory, states and "flags" to communicate these states to neighbors in viewing range. They gather in time $\mathcal{O}(n)$. In this paper we contribute the (to the best of our knowledge) first gathering algorithm on the grid that works under the same simple local model as the above mentioned Euclidean plane strategy, i.e., without memory (oblivious), "flags" and states. We prove its correctness and an $\mathcal{O}(n^2)$ time bound in the fully synchronous $\mathcal{FSYNC}$ time model. This time bound matches the time bound of the best known algorithm for the Euclidean plane mentioned above. We say gathering is done if all robots are located within a $2\times 2$ square, because in $\mathcal{FSYNC}$ such configurations cannot be solved.