Matthias Fischer
Gathering Anonymous, Oblivious Robots on a Grid
Aug 03, 2017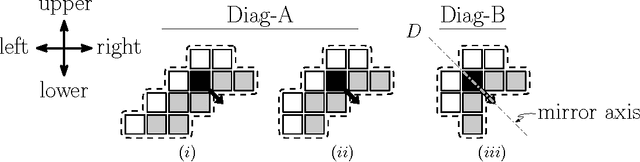
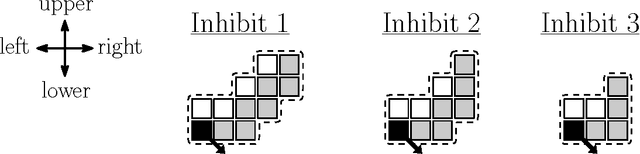

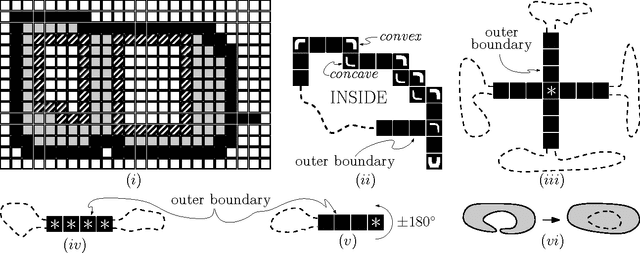
Abstract:We consider a swarm of $n$ autonomous mobile robots, distributed on a 2-dimensional grid. A basic task for such a swarm is the gathering process: All robots have to gather at one (not predefined) place. A common local model for extremely simple robots is the following: The robots do not have a common compass, only have a constant viewing radius, are autonomous and indistinguishable, can move at most a constant distance in each step, cannot communicate, are oblivious and do not have flags or states. The only gathering algorithm under this robot model, with known runtime bounds, needs $\mathcal{O}(n^2)$ rounds and works in the Euclidean plane. The underlying time model for the algorithm is the fully synchronous $\mathcal{FSYNC}$ model. On the other side, in the case of the 2-dimensional grid, the only known gathering algorithms for the same time and a similar local model additionally require a constant memory, states and "flags" to communicate these states to neighbors in viewing range. They gather in time $\mathcal{O}(n)$. In this paper we contribute the (to the best of our knowledge) first gathering algorithm on the grid that works under the same simple local model as the above mentioned Euclidean plane strategy, i.e., without memory (oblivious), "flags" and states. We prove its correctness and an $\mathcal{O}(n^2)$ time bound in the fully synchronous $\mathcal{FSYNC}$ time model. This time bound matches the time bound of the best known algorithm for the Euclidean plane mentioned above. We say gathering is done if all robots are located within a $2\times 2$ square, because in $\mathcal{FSYNC}$ such configurations cannot be solved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge