Stability-Informed Initialization of Neural Ordinary Differential Equations

This paper addresses the training of Neural Ordinary Differential Equations (neural ODEs), and in particular explores the interplay between numerical integration techniques, stability regions, step size, and initialization techniques. It is shown how the choice of integration technique implicitly regularizes the learned model, and how the solver's corresponding stability region affects training and prediction performance. From this analysis, a stability-informed parameter initialization technique is introduced. The effectiveness of the initialization method is displayed across several learning benchmarks and industrial applications.

Analysis of Numerical Integration in RNN-Based Residuals for Fault Diagnosis of Dynamic Systems

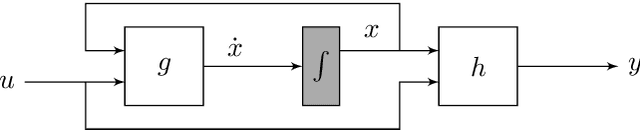
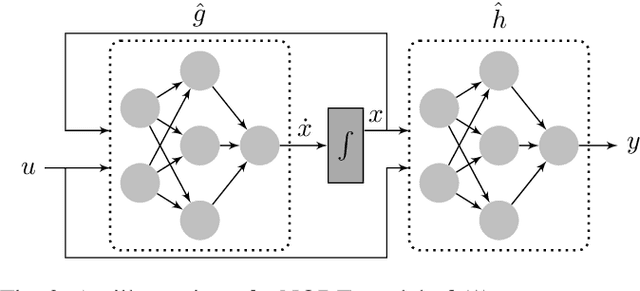
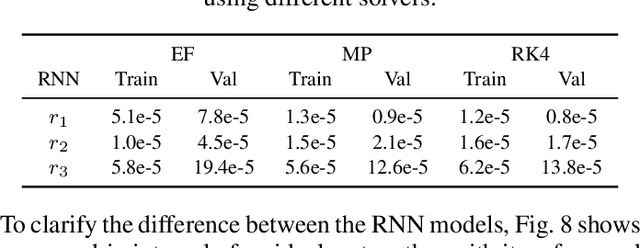
Data-driven modeling and machine learning are widely used to model the behavior of dynamic systems. One application is the residual evaluation of technical systems where model predictions are compared with measurement data to create residuals for fault diagnosis applications. While recurrent neural network models have been shown capable of modeling complex non-linear dynamic systems, they are limited to fixed steps discrete-time simulation. Modeling using neural ordinary differential equations, however, make it possible to evaluate the state variables at specific times, compute gradients when training the model and use standard numerical solvers to explicitly model the underlying dynamic of the time-series data. Here, the effect of solver selection on the performance of neural ordinary differential equation residuals during training and evaluation is investigated. The paper includes a case study of a heavy-duty truck's after-treatment system to highlight the potential of these techniques for improving fault diagnosis performance.

Data-Driven Open Set Fault Classification and Fault Size Estimation Using Quantitative Fault Diagnosis Analysis

Data-driven fault classification is complicated by imbalanced training data and unknown fault classes. Fault diagnosis of dynamic systems is done by detecting changes in time-series data, for example residuals, caused by faults or system degradation. Different fault classes can result in similar residual outputs, especially for small faults which can be difficult to distinguish from nominal system operation. Analyzing how easy it is to distinguish data from different fault classes is crucial during the design process of a diagnosis system to evaluate if classification performance requirements can be met. Here, a data-driven model of different fault classes is used based on the Kullback-Leibler divergence. This is used to develop a framework for quantitative fault diagnosis performance analysis and open set fault classification. A data-driven fault classification algorithm is proposed which can handle unknown faults and also estimate the fault size using training data from known fault scenarios. To illustrate the usefulness of the proposed methods, data have been collected from an engine test bench to illustrate the design process of a data-driven diagnosis system, including quantitative fault diagnosis analysis and evaluation of the developed open set fault classification algorithm.

Residual Generation Using Physically-Based Grey-Box Recurrent Neural Networks For Engine Fault Diagnosis

Data-driven fault diagnosis is complicated by unknown fault classes and limited training data from different fault realizations. In these situations, conventional multi-class classification approaches are not suitable for fault diagnosis. One solution is the use of anomaly classifiers that are trained using only nominal data. Anomaly classifiers can be used to detect when a fault occurs but give little information about its root cause. Hybrid fault diagnosis methods combining physically-based models and available training data have shown promising results to improve fault classification performance and identify unknown fault classes. Residual generation using grey-box recurrent neural networks can be used for anomaly classification where physical insights about the monitored system are incorporated into the design of the machine learning algorithm. In this work, an automated residual design is developed using a bipartite graph representation of the system model to design grey-box recurrent neural networks and evaluated using a real industrial case study. Data from an internal combustion engine test bench is used to illustrate the potentials of combining machine learning and model-based fault diagnosis techniques.

Isolation and Localization of Unknown Faults Using Neural Network-Based Residuals

Localization of unknown faults in industrial systems is a difficult task for data-driven diagnosis methods. The classification performance of many machine learning methods relies on the quality of training data. Unknown faults, for example faults not represented in training data, can be detected using, for example, anomaly classifiers. However, mapping these unknown faults to an actual location in the real system is a non-trivial problem. In model-based diagnosis, physical-based models are used to create residuals that isolate faults by mapping model equations to faulty system components. Developing sufficiently accurate physical-based models can be a time-consuming process. Hybrid modeling methods combining physical-based methods and machine learning is one solution to design data-driven residuals for fault isolation. In this work, a set of neural network-based residuals are designed by incorporating physical insights about the system behavior in the residual model structure. The residuals are trained using only fault-free data and a simulation case study shows that they can be used to perform fault isolation and localization of unknown faults in the system.

Gathering Anonymous, Oblivious Robots on a Grid

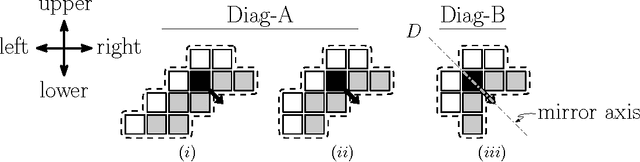
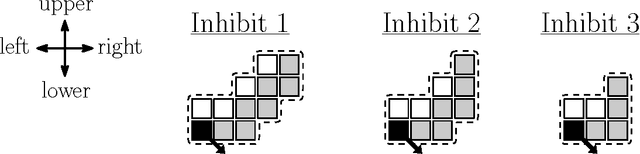
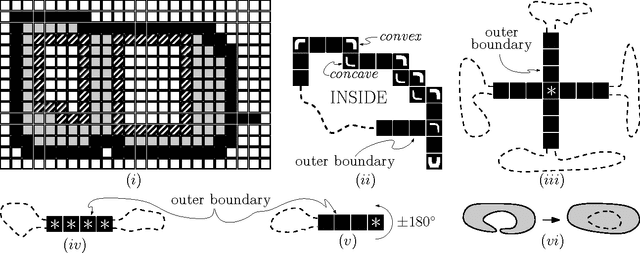
We consider a swarm of $n$ autonomous mobile robots, distributed on a 2-dimensional grid. A basic task for such a swarm is the gathering process: All robots have to gather at one (not predefined) place. A common local model for extremely simple robots is the following: The robots do not have a common compass, only have a constant viewing radius, are autonomous and indistinguishable, can move at most a constant distance in each step, cannot communicate, are oblivious and do not have flags or states. The only gathering algorithm under this robot model, with known runtime bounds, needs $\mathcal{O}(n^2)$ rounds and works in the Euclidean plane. The underlying time model for the algorithm is the fully synchronous $\mathcal{FSYNC}$ model. On the other side, in the case of the 2-dimensional grid, the only known gathering algorithms for the same time and a similar local model additionally require a constant memory, states and "flags" to communicate these states to neighbors in viewing range. They gather in time $\mathcal{O}(n)$. In this paper we contribute the (to the best of our knowledge) first gathering algorithm on the grid that works under the same simple local model as the above mentioned Euclidean plane strategy, i.e., without memory (oblivious), "flags" and states. We prove its correctness and an $\mathcal{O}(n^2)$ time bound in the fully synchronous $\mathcal{FSYNC}$ time model. This time bound matches the time bound of the best known algorithm for the Euclidean plane mentioned above. We say gathering is done if all robots are located within a $2\times 2$ square, because in $\mathcal{FSYNC}$ such configurations cannot be solved.