Usage-Specific Survival Modeling Based on Operational Data and Neural Networks

Accurate predictions of when a component will fail are crucial when planning maintenance, and by modeling the distribution of these failure times, survival models have shown to be particularly useful in this context. The presented methodology is based on conventional neural network-based survival models that are trained using data that is continuously gathered and stored at specific times, called snapshots. An important property of this type of training data is that it can contain more than one snapshot from a specific individual which results in that standard maximum likelihood training can not be directly applied since the data is not independent. However, the papers show that if the data is in a specific format where all snapshot times are the same for all individuals, called homogeneously sampled, maximum likelihood training can be applied and produce desirable results. In many cases, the data is not homogeneously sampled and in this case, it is proposed to resample the data to make it homogeneously sampled. How densely the dataset is sampled turns out to be an important parameter; it should be chosen large enough to produce good results, but this also increases the size of the dataset which makes training slow. To reduce the number of samples needed during training, the paper also proposes a technique to, instead of resampling the dataset once before the training starts, randomly resample the dataset at the start of each epoch during the training. The proposed methodology is evaluated on both a simulated dataset and an experimental dataset of starter battery failures. The results show that if the data is homogeneously sampled the methodology works as intended and produces accurate survival models. The results also show that randomly resampling the dataset on each epoch is an effective way to reduce the size of the training data.

Neural Network-Based Piecewise Survival Models

In this paper, a family of neural network-based survival models is presented. The models are specified based on piecewise definitions of the hazard function and the density function on a partitioning of the time; both constant and linear piecewise definitions are presented, resulting in a family of four models. The models can be seen as an extension of the commonly used discrete-time and piecewise exponential models and thereby add flexibility to this set of standard models. Using a simulated dataset the models are shown to perform well compared to the highly expressive, state-of-the-art energy-based model, while only requiring a fraction of the computation time.

Analysis of Numerical Integration in RNN-Based Residuals for Fault Diagnosis of Dynamic Systems

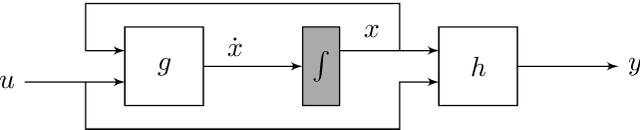
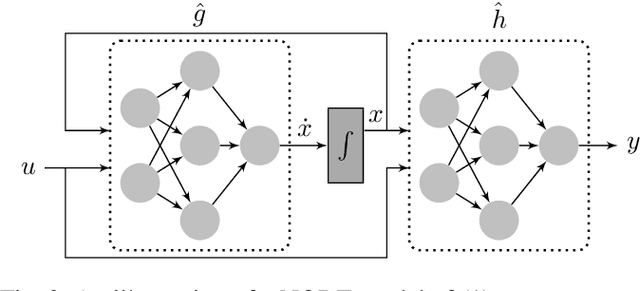
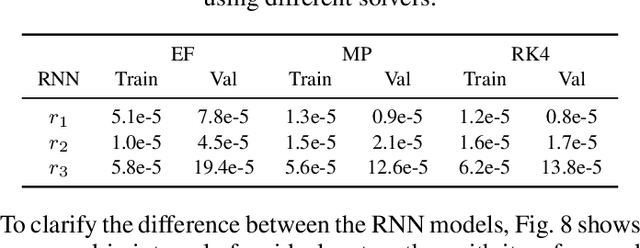
Data-driven modeling and machine learning are widely used to model the behavior of dynamic systems. One application is the residual evaluation of technical systems where model predictions are compared with measurement data to create residuals for fault diagnosis applications. While recurrent neural network models have been shown capable of modeling complex non-linear dynamic systems, they are limited to fixed steps discrete-time simulation. Modeling using neural ordinary differential equations, however, make it possible to evaluate the state variables at specific times, compute gradients when training the model and use standard numerical solvers to explicitly model the underlying dynamic of the time-series data. Here, the effect of solver selection on the performance of neural ordinary differential equation residuals during training and evaluation is investigated. The paper includes a case study of a heavy-duty truck's after-treatment system to highlight the potential of these techniques for improving fault diagnosis performance.

Time Series Fault Classification for Wave Propagation Systems with Sparse Fault Data

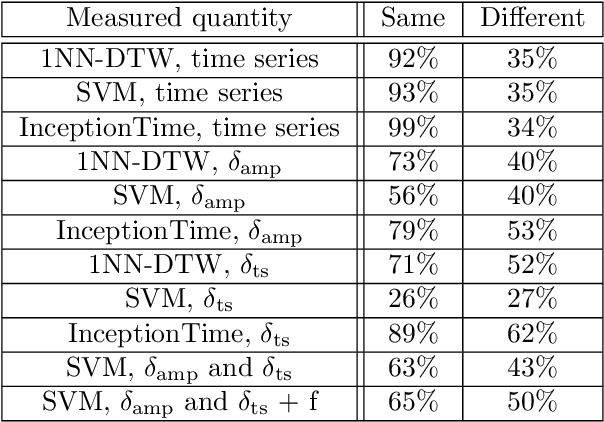
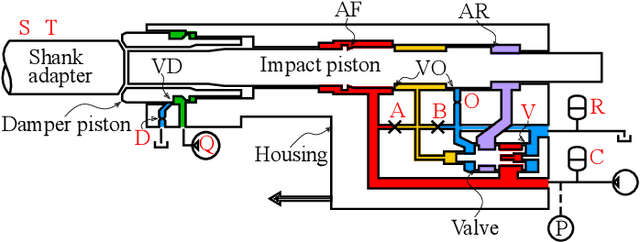
In this work Time Series Classification techniques are investigated, and especially their applicability in applications where there are significant differences between the individuals where data is collected, and the individuals where the classification is evaluated. Classification methods are applied to a fault classification case, where a key assumption is that data from a fault free reference case for each specific individual is available. For the investigated application, wave propagation cause almost chaotic changes of a measured pressure signal, and physical modeling is difficult. Direct application of One-Nearest-Neighbor Dynamic Time Warping, a common technique for this kind of problem, and other machine learning techniques are shown to fail for this case and new methods to improve the situation are presented. By using relative features describing the difference from the reference case rather than the absolute time series, improvements are made compared to state-of-the-art time series classification algorithms.