Scalable Bayesian Inference for Detection and Deblending in Astronomical Images

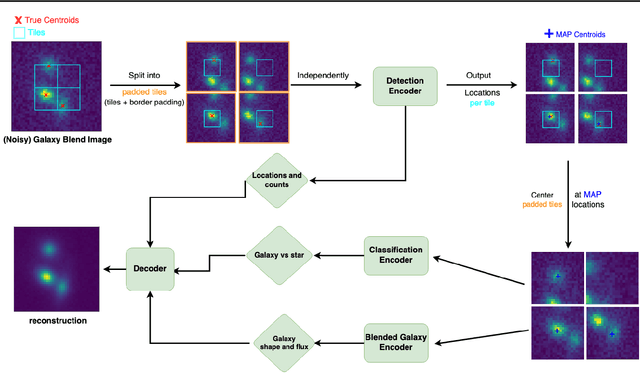
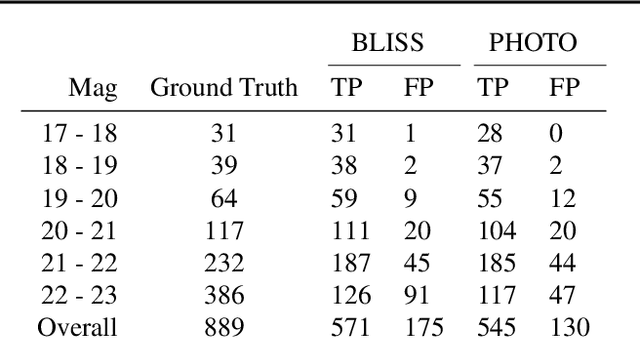
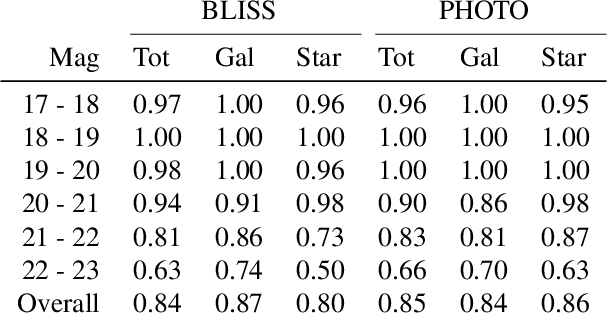
We present a new probabilistic method for detecting, deblending, and cataloging astronomical sources called the Bayesian Light Source Separator (BLISS). BLISS is based on deep generative models, which embed neural networks within a Bayesian model. For posterior inference, BLISS uses a new form of variational inference known as Forward Amortized Variational Inference. The BLISS inference routine is fast, requiring a single forward pass of the encoder networks on a GPU once the encoder networks are trained. BLISS can perform fully Bayesian inference on megapixel images in seconds, and produces highly accurate catalogs. BLISS is highly extensible, and has the potential to directly answer downstream scientific questions in addition to producing probabilistic catalogs.

Evaluating Sensitivity to the Stick-Breaking Prior in Bayesian Nonparametrics

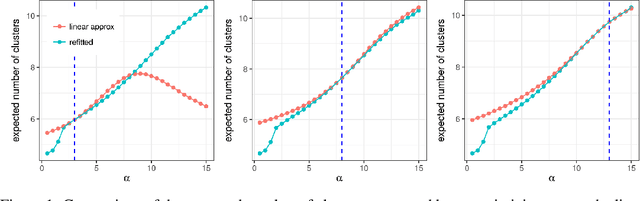
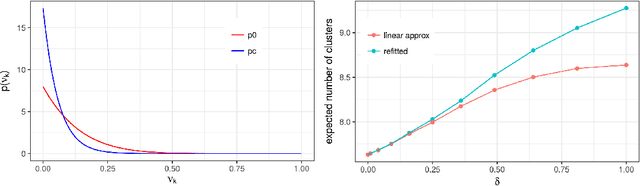
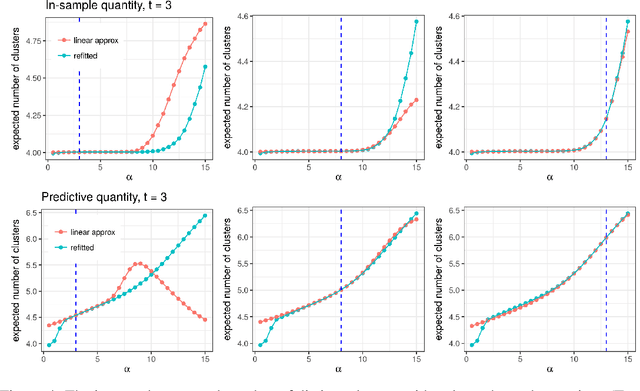
Bayesian models based on the Dirichlet process and other stick-breaking priors have been proposed as core ingredients for clustering, topic modeling, and other unsupervised learning tasks. Prior specification is, however, relatively difficult for such models, given that their flexibility implies that the consequences of prior choices are often relatively opaque. Moreover, these choices can have a substantial effect on posterior inferences. Thus, considerations of robustness need to go hand in hand with nonparametric modeling. In the current paper, we tackle this challenge by exploiting the fact that variational Bayesian methods, in addition to having computational advantages in fitting complex nonparametric models, also yield sensitivities with respect to parametric and nonparametric aspects of Bayesian models. In particular, we demonstrate how to assess the sensitivity of conclusions to the choice of concentration parameter and stick-breaking distribution for inferences under Dirichlet process mixtures and related mixture models. We provide both theoretical and empirical support for our variational approach to Bayesian sensitivity analysis.

Variational Inference for Deblending Crowded Starfields

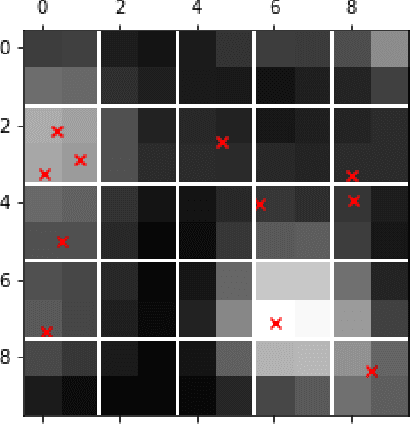
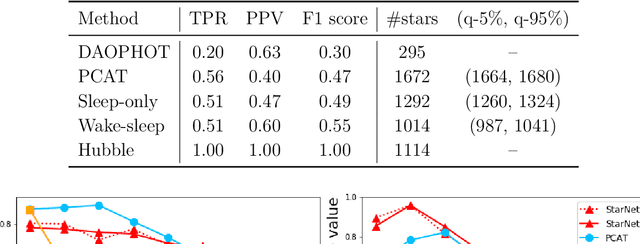
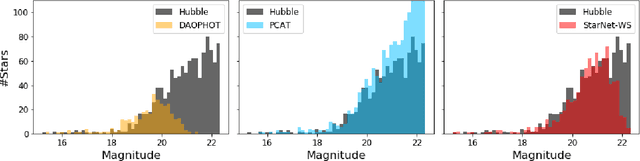
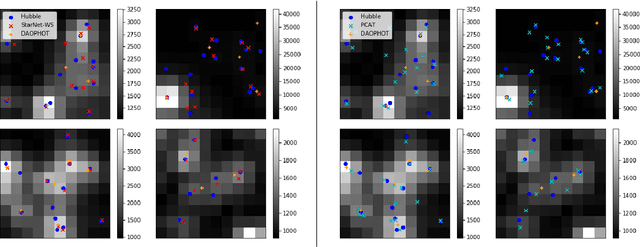
In the image data collected by astronomical surveys, stars and galaxies often overlap. Deblending is the task of distinguishing and characterizing individual light sources from survey images. We propose StarNet, a fully Bayesian method to deblend sources in astronomical images of crowded star fields. StarNet leverages recent advances in variational inference, including amortized variational distributions and the wake-sleep algorithm. Wake-sleep, which minimizes forward KL divergence, has significant benefits compared to traditional variational inference, which minimizes a reverse KL divergence. In our experiments with SDSS images of the M2 globular cluster, StarNet is substantially more accurate than two competing methods: Probablistic Cataloging (PCAT), a method that uses MCMC for inference, and a software pipeline employed by SDSS for deblending (DAOPHOT). In addition, StarNet is as much as $100,000$ times faster than PCAT, exhibiting the scaling characteristics necessary to perform fully Bayesian inference on modern astronomical surveys.

Rao-Blackwellized Stochastic Gradients for Discrete Distributions

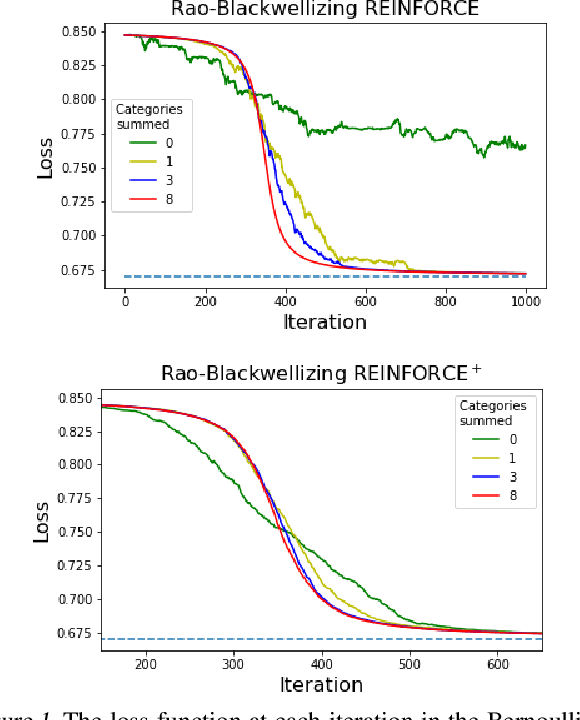
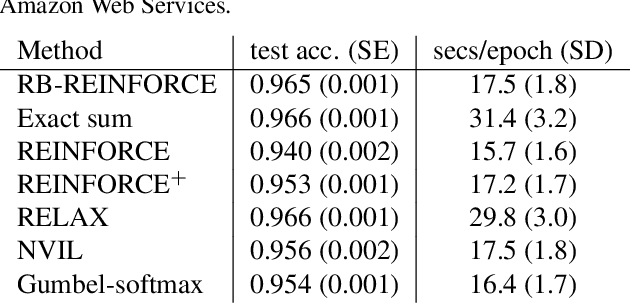
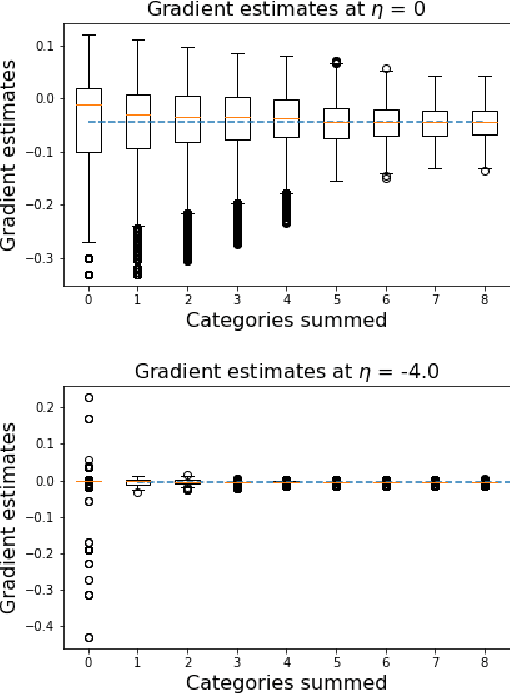
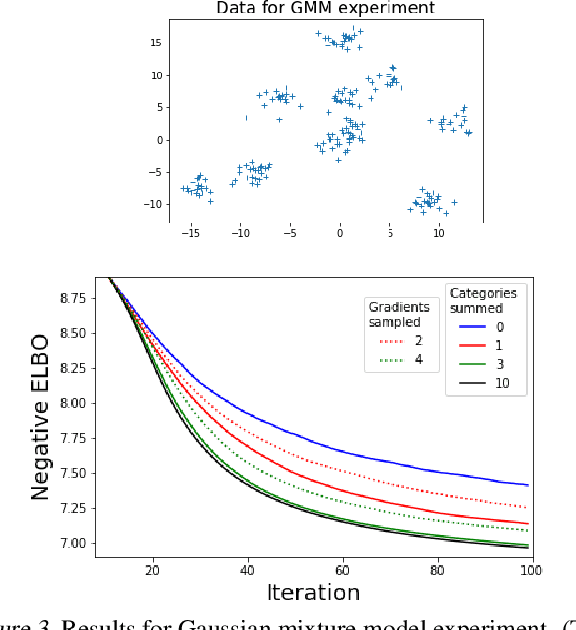
We wish to compute the gradient of an expectation over a finite or countably infinite sample space having $K \leq \infty$ categories. When $K$ is indeed infinite, or finite but very large, the relevant summation is intractable. Accordingly, various stochastic gradient estimators have been proposed. In this paper, we describe a technique that can be applied to reduce the variance of any such estimator, without changing its bias---in particular, unbiasedness is retained. We show that our technique is an instance of Rao-Blackwellization, and we demonstrate the improvement it yields in empirical studies on both synthetic and real-world data.