Variational Inference for Deblending Crowded Starfields

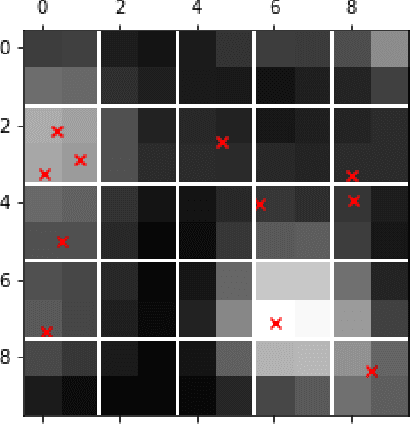
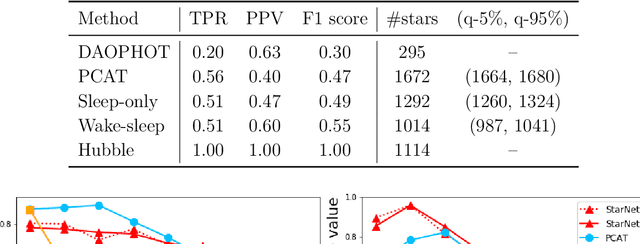
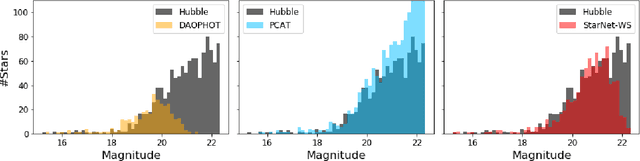
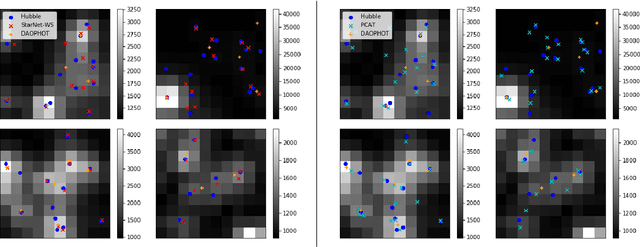
In the image data collected by astronomical surveys, stars and galaxies often overlap. Deblending is the task of distinguishing and characterizing individual light sources from survey images. We propose StarNet, a fully Bayesian method to deblend sources in astronomical images of crowded star fields. StarNet leverages recent advances in variational inference, including amortized variational distributions and the wake-sleep algorithm. Wake-sleep, which minimizes forward KL divergence, has significant benefits compared to traditional variational inference, which minimizes a reverse KL divergence. In our experiments with SDSS images of the M2 globular cluster, StarNet is substantially more accurate than two competing methods: Probablistic Cataloging (PCAT), a method that uses MCMC for inference, and a software pipeline employed by SDSS for deblending (DAOPHOT). In addition, StarNet is as much as $100,000$ times faster than PCAT, exhibiting the scaling characteristics necessary to perform fully Bayesian inference on modern astronomical surveys.

Approximate Inference for Constructing Astronomical Catalogs from Images

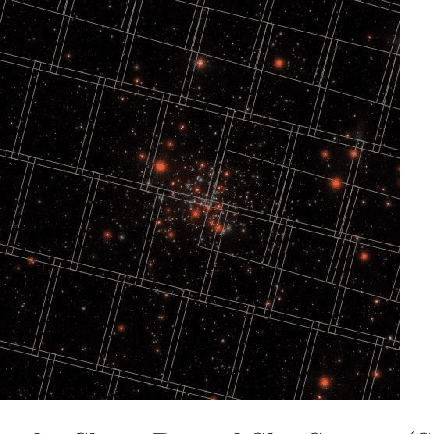
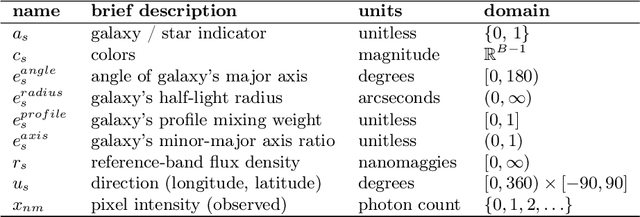
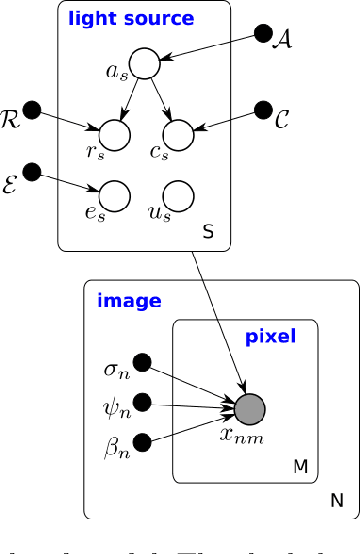
We present a new, fully generative model for constructing astronomical catalogs from optical telescope image sets. Each pixel intensity is treated as a Poisson random variable with a rate parameter that depends on the latent properties of stars and galaxies. These latent properties are themselves random, with prior distributions fitted by empirical Bayes. We compare two procedures for posterior inference. One procedure is based on Markov chain Monte Carlo (MCMC) while the other is based on variational inference (VI). We demonstrate that the MCMC procedure excels at quantifying uncertainty while the VI procedure is 1000x faster. For the error metric we consider, both procedures outperform the current state-of-the-art method for measuring the colors, shapes, and morphologies of stars and galaxies. On a supercomputer, the VI procedure efficiently uses 665,000 CPU cores (1.3 million hardware threads) to construct an astronomical catalog from 50 terabytes of images

Variational Inference: A Review for Statisticians

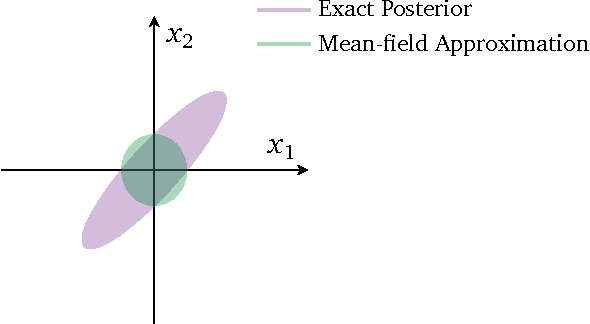
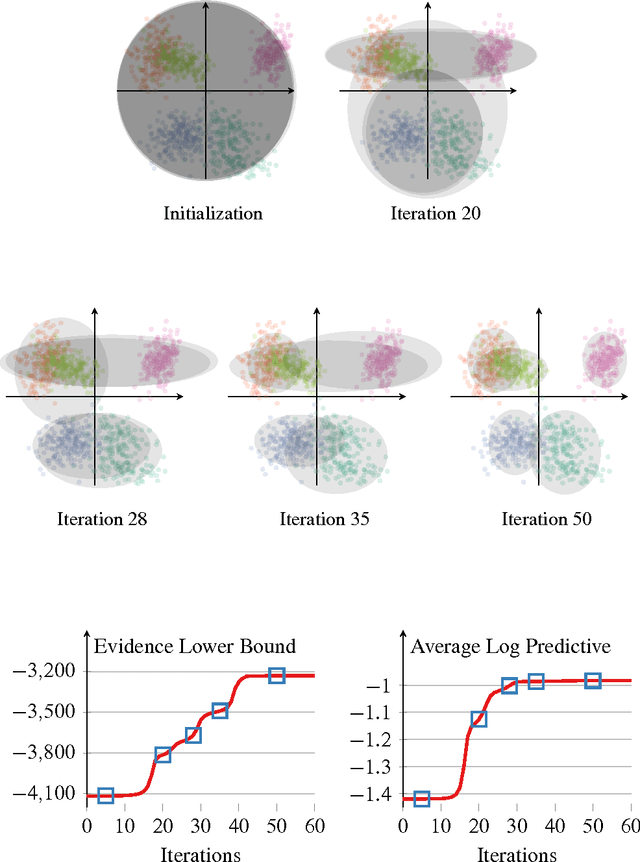
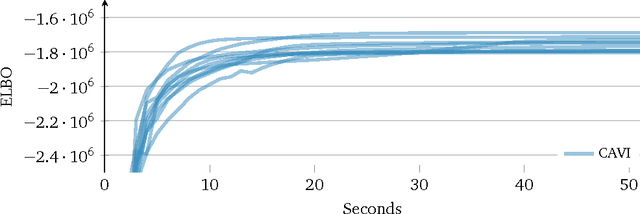
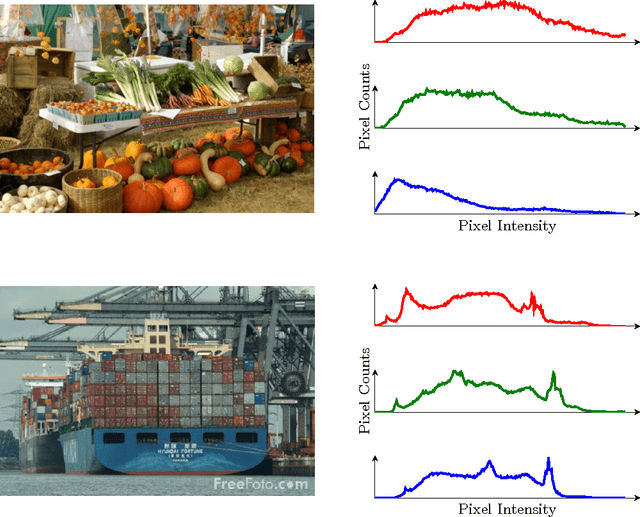
One of the core problems of modern statistics is to approximate difficult-to-compute probability densities. This problem is especially important in Bayesian statistics, which frames all inference about unknown quantities as a calculation involving the posterior density. In this paper, we review variational inference (VI), a method from machine learning that approximates probability densities through optimization. VI has been used in many applications and tends to be faster than classical methods, such as Markov chain Monte Carlo sampling. The idea behind VI is to first posit a family of densities and then to find the member of that family which is close to the target. Closeness is measured by Kullback-Leibler divergence. We review the ideas behind mean-field variational inference, discuss the special case of VI applied to exponential family models, present a full example with a Bayesian mixture of Gaussians, and derive a variant that uses stochastic optimization to scale up to massive data. We discuss modern research in VI and highlight important open problems. VI is powerful, but it is not yet well understood. Our hope in writing this paper is to catalyze statistical research on this class of algorithms.

Supervised Topic Models

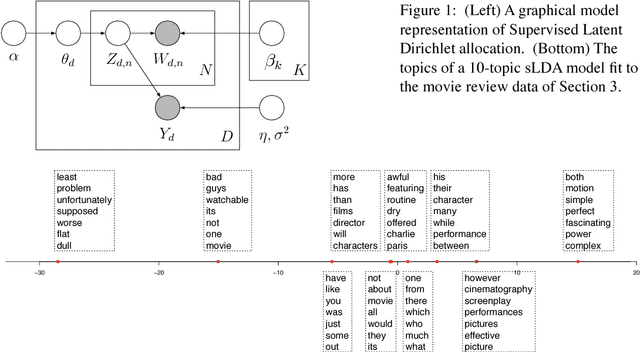
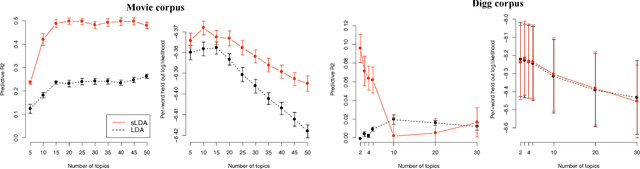
We introduce supervised latent Dirichlet allocation (sLDA), a statistical model of labelled documents. The model accommodates a variety of response types. We derive an approximate maximum-likelihood procedure for parameter estimation, which relies on variational methods to handle intractable posterior expectations. Prediction problems motivate this research: we use the fitted model to predict response values for new documents. We test sLDA on two real-world problems: movie ratings predicted from reviews, and the political tone of amendments in the U.S. Senate based on the amendment text. We illustrate the benefits of sLDA versus modern regularized regression, as well as versus an unsupervised LDA analysis followed by a separate regression.