Approximate Inference for Constructing Astronomical Catalogs from Images

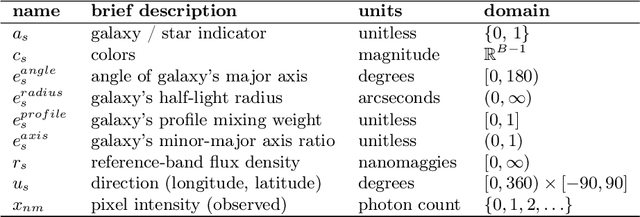
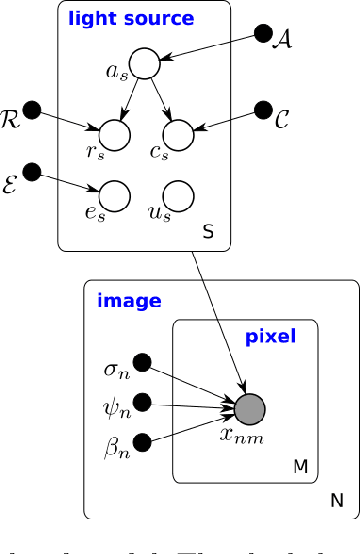
We present a new, fully generative model for constructing astronomical catalogs from optical telescope image sets. Each pixel intensity is treated as a Poisson random variable with a rate parameter that depends on the latent properties of stars and galaxies. These latent properties are themselves random, with prior distributions fitted by empirical Bayes. We compare two procedures for posterior inference. One procedure is based on Markov chain Monte Carlo (MCMC) while the other is based on variational inference (VI). We demonstrate that the MCMC procedure excels at quantifying uncertainty while the VI procedure is 1000x faster. For the error metric we consider, both procedures outperform the current state-of-the-art method for measuring the colors, shapes, and morphologies of stars and galaxies. On a supercomputer, the VI procedure efficiently uses 665,000 CPU cores (1.3 million hardware threads) to construct an astronomical catalog from 50 terabytes of images