Approximate Inference for Constructing Astronomical Catalogs from Images

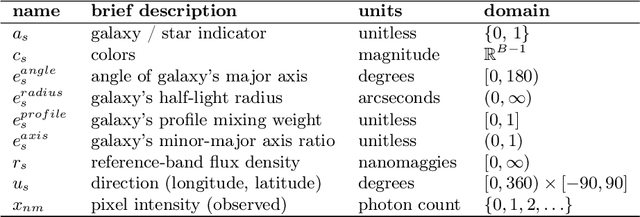
We present a new, fully generative model for constructing astronomical catalogs from optical telescope image sets. Each pixel intensity is treated as a Poisson random variable with a rate parameter that depends on the latent properties of stars and galaxies. These latent properties are themselves random, with prior distributions fitted by empirical Bayes. We compare two procedures for posterior inference. One procedure is based on Markov chain Monte Carlo (MCMC) while the other is based on variational inference (VI). We demonstrate that the MCMC procedure excels at quantifying uncertainty while the VI procedure is 1000x faster. For the error metric we consider, both procedures outperform the current state-of-the-art method for measuring the colors, shapes, and morphologies of stars and galaxies. On a supercomputer, the VI procedure efficiently uses 665,000 CPU cores (1.3 million hardware threads) to construct an astronomical catalog from 50 terabytes of images

Learning an Astronomical Catalog of the Visible Universe through Scalable Bayesian Inference

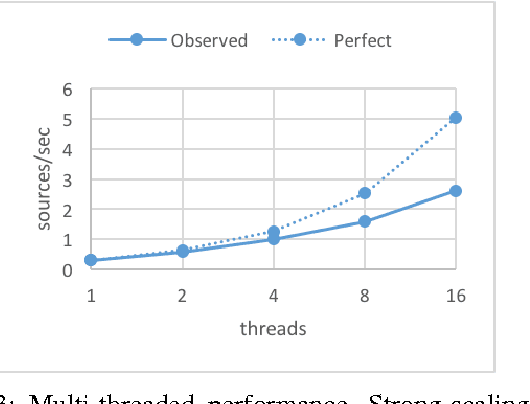
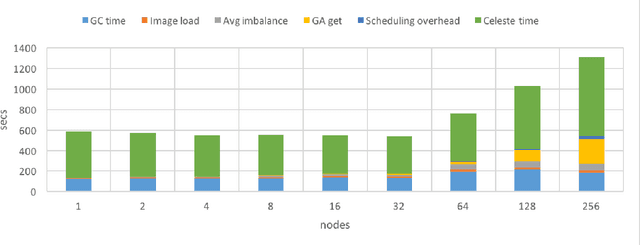
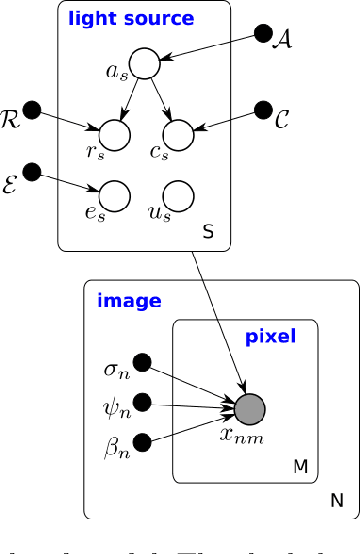
Celeste is a procedure for inferring astronomical catalogs that attains state-of-the-art scientific results. To date, Celeste has been scaled to at most hundreds of megabytes of astronomical images: Bayesian posterior inference is notoriously demanding computationally. In this paper, we report on a scalable, parallel version of Celeste, suitable for learning catalogs from modern large-scale astronomical datasets. Our algorithmic innovations include a fast numerical optimization routine for Bayesian posterior inference and a statistically efficient scheme for decomposing astronomical optimization problems into subproblems. Our scalable implementation is written entirely in Julia, a new high-level dynamic programming language designed for scientific and numerical computing. We use Julia's high-level constructs for shared and distributed memory parallelism, and demonstrate effective load balancing and efficient scaling on up to 8192 Xeon cores on the NERSC Cori supercomputer.

Celeste: Variational inference for a generative model of astronomical images

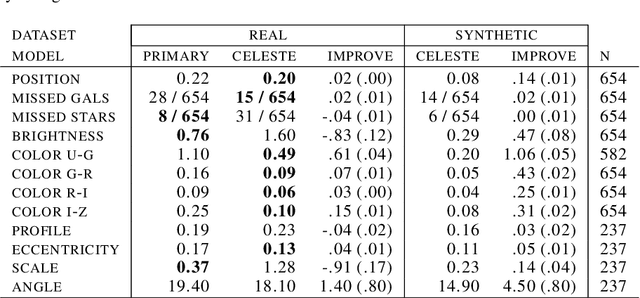
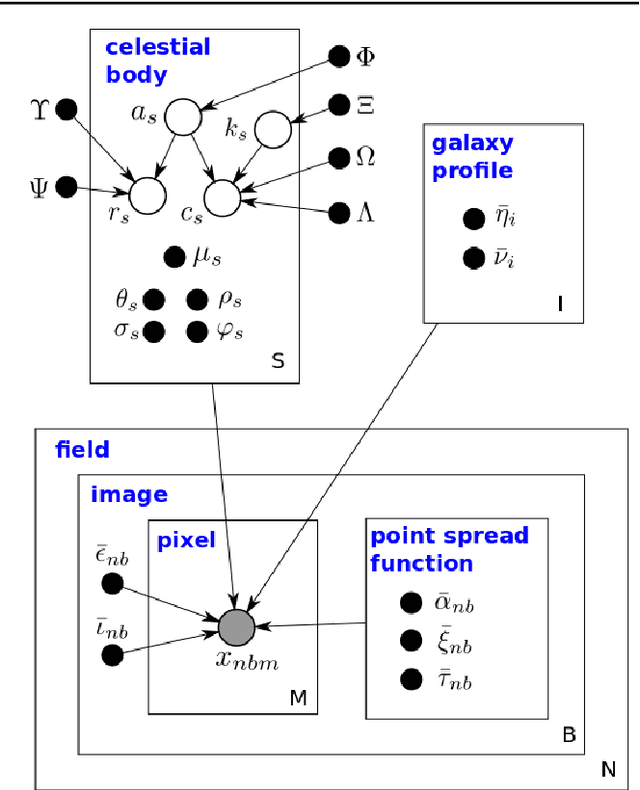
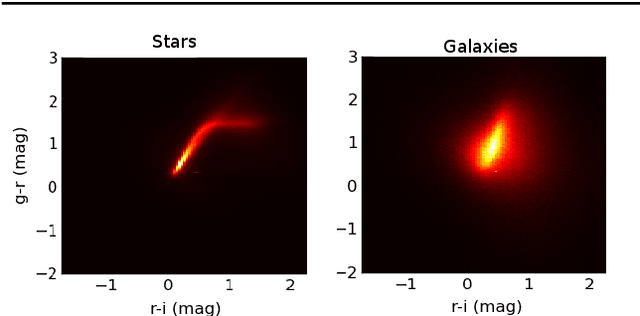
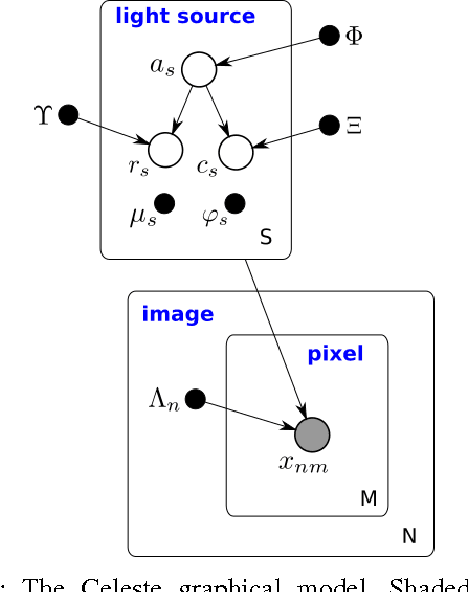
We present a new, fully generative model of optical telescope image sets, along with a variational procedure for inference. Each pixel intensity is treated as a Poisson random variable, with a rate parameter dependent on latent properties of stars and galaxies. Key latent properties are themselves random, with scientific prior distributions constructed from large ancillary data sets. We check our approach on synthetic images. We also run it on images from a major sky survey, where it exceeds the performance of the current state-of-the-art method for locating celestial bodies and measuring their colors.