Treeffuser: Probabilistic Predictions via Conditional Diffusions with Gradient-Boosted Trees

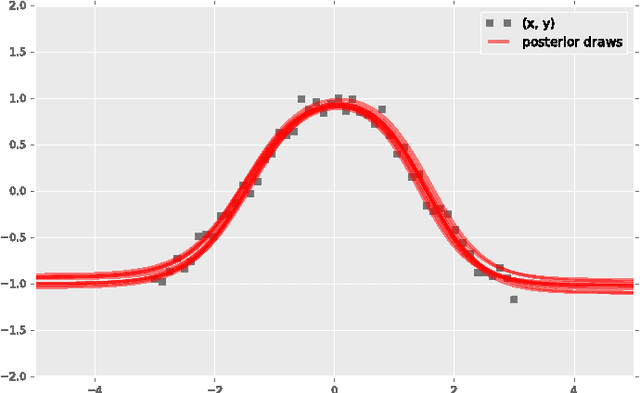
Probabilistic prediction aims to compute predictive distributions rather than single-point predictions. These distributions enable practitioners to quantify uncertainty, compute risk, and detect outliers. However, most probabilistic methods assume parametric responses, such as Gaussian or Poisson distributions. When these assumptions fail, such models lead to bad predictions and poorly calibrated uncertainty. In this paper, we propose Treeffuser, an easy-to-use method for probabilistic prediction on tabular data. The idea is to learn a conditional diffusion model where the score function is estimated using gradient-boosted trees. The conditional diffusion model makes Treeffuser flexible and non-parametric, while the gradient-boosted trees make it robust and easy to train on CPUs. Treeffuser learns well-calibrated predictive distributions and can handle a wide range of regression tasks -- including those with multivariate, multimodal, and skewed responses. % , as well as categorical predictors and missing data We study Treeffuser on synthetic and real data and show that it outperforms existing methods, providing better-calibrated probabilistic predictions. We further demonstrate its versatility with an application to inventory allocation under uncertainty using sales data from Walmart. We implement Treeffuser in \href{https://github.com/blei-lab/treeffuser}{https://github.com/blei-lab/treeffuser}.

Hindsight Expectation Maximization for Goal-conditioned Reinforcement Learning

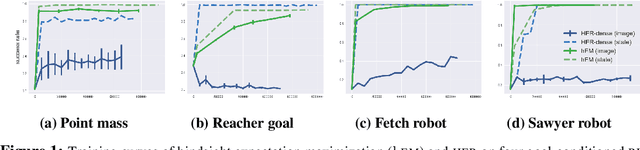
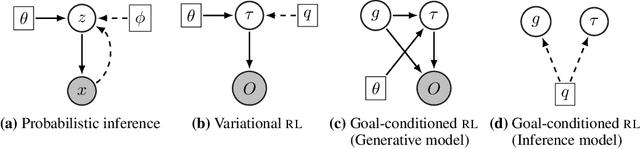
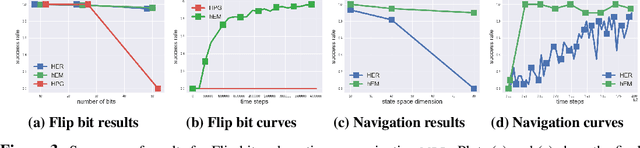
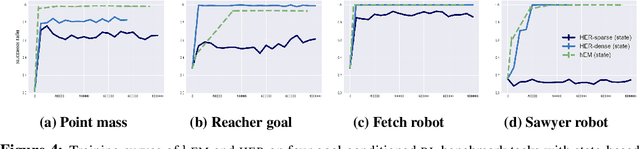
We propose a graphical model framework for goal-conditioned RL, with an EM algorithm that operates on the lower bound of the RL objective. The E-step provides a natural interpretation of how 'learning in hindsight' techniques, such as HER, to handle extremely sparse goal-conditioned rewards. The M-step reduces policy optimization to supervised learning updates, which greatly stabilizes end-to-end training on high-dimensional inputs such as images. We show that the combined algorithm, hEM significantly outperforms model-free baselines on a wide range of goal-conditioned benchmarks with sparse rewards.

Robust Probabilistic Modeling with Bayesian Data Reweighting

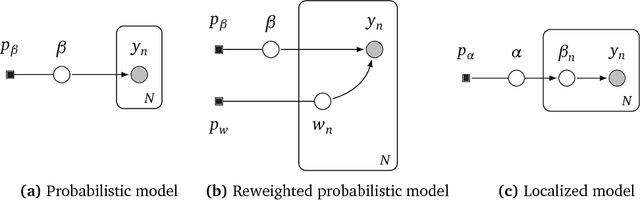
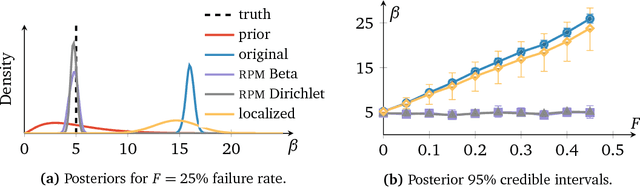
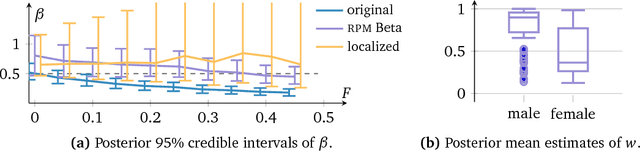
Probabilistic models analyze data by relying on a set of assumptions. Data that exhibit deviations from these assumptions can undermine inference and prediction quality. Robust models offer protection against mismatch between a model's assumptions and reality. We propose a way to systematically detect and mitigate mismatch of a large class of probabilistic models. The idea is to raise the likelihood of each observation to a weight and then to infer both the latent variables and the weights from data. Inferring the weights allows a model to identify observations that match its assumptions and down-weight others. This enables robust inference and improves predictive accuracy. We study four different forms of mismatch with reality, ranging from missing latent groups to structure misspecification. A Poisson factorization analysis of the Movielens 1M dataset shows the benefits of this approach in a practical scenario.

Variational Inference: A Review for Statisticians

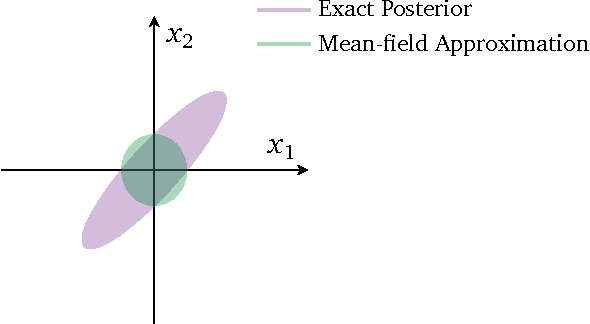
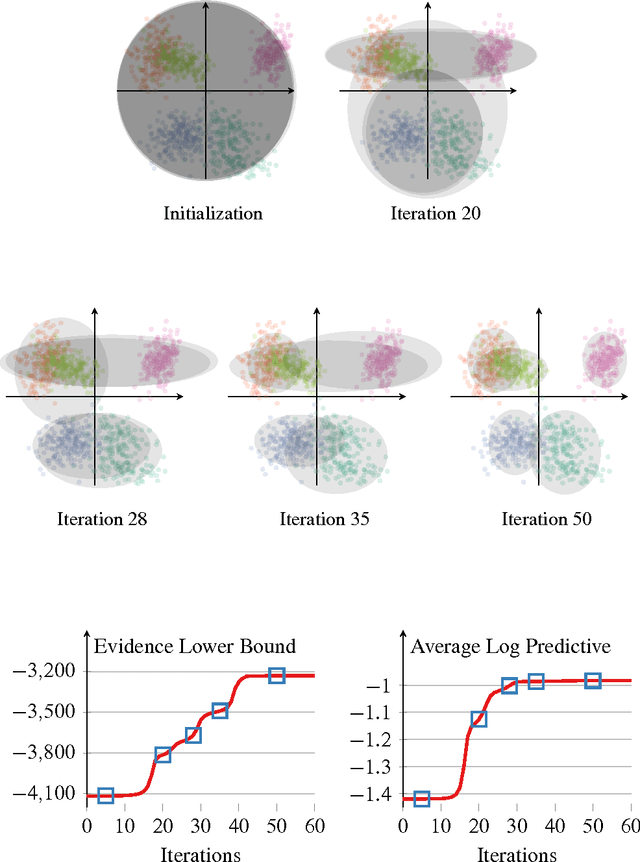
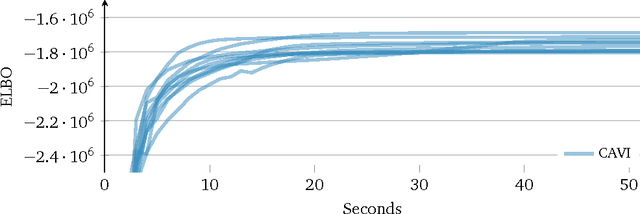
One of the core problems of modern statistics is to approximate difficult-to-compute probability densities. This problem is especially important in Bayesian statistics, which frames all inference about unknown quantities as a calculation involving the posterior density. In this paper, we review variational inference (VI), a method from machine learning that approximates probability densities through optimization. VI has been used in many applications and tends to be faster than classical methods, such as Markov chain Monte Carlo sampling. The idea behind VI is to first posit a family of densities and then to find the member of that family which is close to the target. Closeness is measured by Kullback-Leibler divergence. We review the ideas behind mean-field variational inference, discuss the special case of VI applied to exponential family models, present a full example with a Bayesian mixture of Gaussians, and derive a variant that uses stochastic optimization to scale up to massive data. We discuss modern research in VI and highlight important open problems. VI is powerful, but it is not yet well understood. Our hope in writing this paper is to catalyze statistical research on this class of algorithms.

Variational Deep Q Network

We propose a framework that directly tackles the probability distribution of the value function parameters in Deep Q Network (DQN), with powerful variational inference subroutines to approximate the posterior of the parameters. We will establish the equivalence between our proposed surrogate objective and variational inference loss. Our new algorithm achieves efficient exploration and performs well on large scale chain Markov Decision Process (MDP).

Edward: A library for probabilistic modeling, inference, and criticism

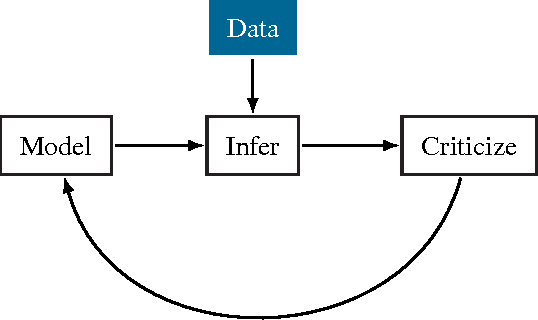
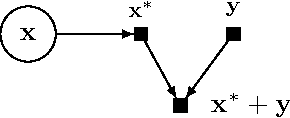
Probabilistic modeling is a powerful approach for analyzing empirical information. We describe Edward, a library for probabilistic modeling. Edward's design reflects an iterative process pioneered by George Box: build a model of a phenomenon, make inferences about the model given data, and criticize the model's fit to the data. Edward supports a broad class of probabilistic models, efficient algorithms for inference, and many techniques for model criticism. The library builds on top of TensorFlow to support distributed training and hardware such as GPUs. Edward enables the development of complex probabilistic models and their algorithms at a massive scale.

Posterior Dispersion Indices

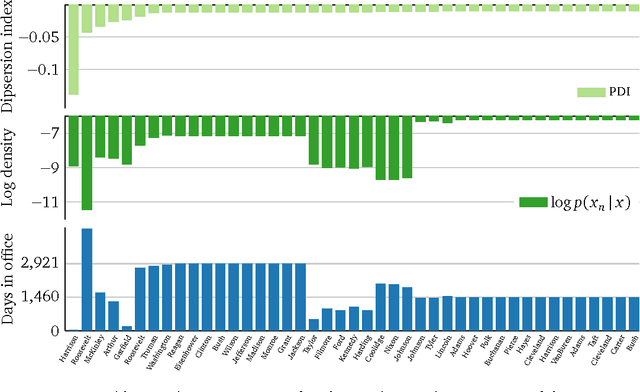
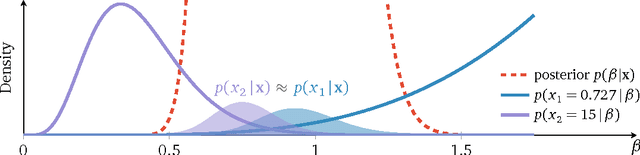
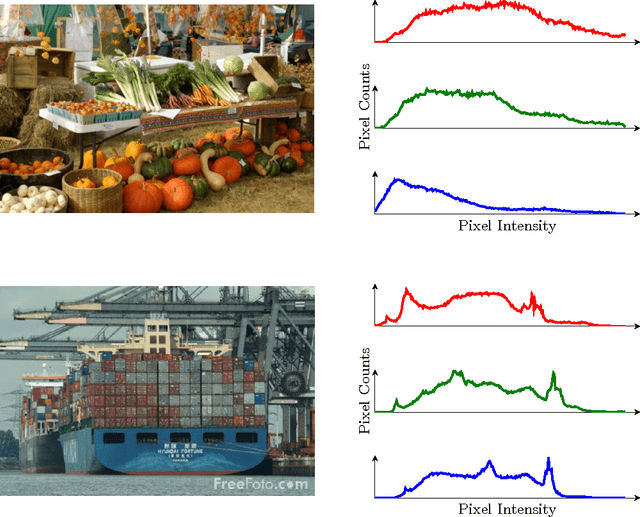
Probabilistic modeling is cyclical: we specify a model, infer its posterior, and evaluate its performance. Evaluation drives the cycle, as we revise our model based on how it performs. This requires a metric. Traditionally, predictive accuracy prevails. Yet, predictive accuracy does not tell the whole story. We propose to evaluate a model through posterior dispersion. The idea is to analyze how each datapoint fares in relation to posterior uncertainty around the hidden structure. We propose a family of posterior dispersion indices (PDI) that capture this idea. A PDI identifies rich patterns of model mismatch in three real data examples: voting preferences, supermarket shopping, and population genetics.

Automatic Differentiation Variational Inference

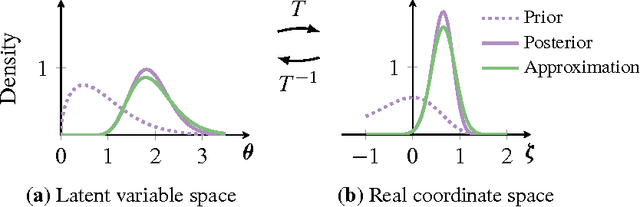
Probabilistic modeling is iterative. A scientist posits a simple model, fits it to her data, refines it according to her analysis, and repeats. However, fitting complex models to large data is a bottleneck in this process. Deriving algorithms for new models can be both mathematically and computationally challenging, which makes it difficult to efficiently cycle through the steps. To this end, we develop automatic differentiation variational inference (ADVI). Using our method, the scientist only provides a probabilistic model and a dataset, nothing else. ADVI automatically derives an efficient variational inference algorithm, freeing the scientist to refine and explore many models. ADVI supports a broad class of models-no conjugacy assumptions are required. We study ADVI across ten different models and apply it to a dataset with millions of observations. ADVI is integrated into Stan, a probabilistic programming system; it is available for immediate use.

Automatic Variational Inference in Stan

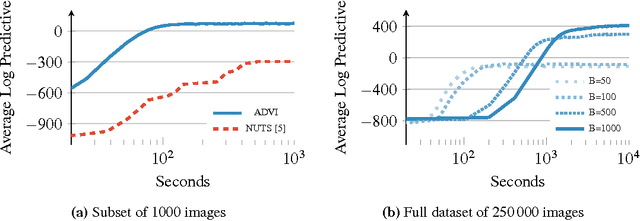
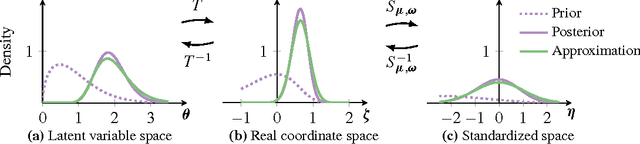
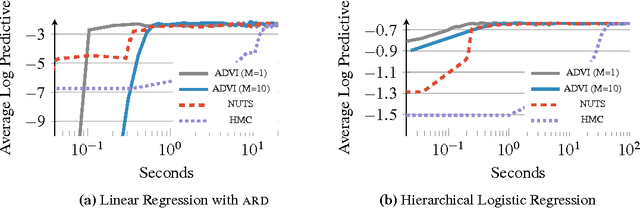
Variational inference is a scalable technique for approximate Bayesian inference. Deriving variational inference algorithms requires tedious model-specific calculations; this makes it difficult to automate. We propose an automatic variational inference algorithm, automatic differentiation variational inference (ADVI). The user only provides a Bayesian model and a dataset; nothing else. We make no conjugacy assumptions and support a broad class of models. The algorithm automatically determines an appropriate variational family and optimizes the variational objective. We implement ADVI in Stan (code available now), a probabilistic programming framework. We compare ADVI to MCMC sampling across hierarchical generalized linear models, nonconjugate matrix factorization, and a mixture model. We train the mixture model on a quarter million images. With ADVI we can use variational inference on any model we write in Stan.

Population Empirical Bayes

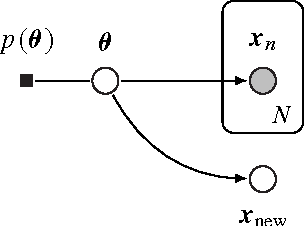
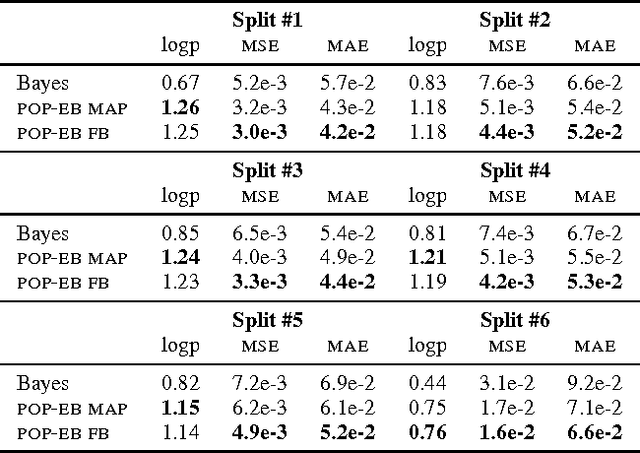
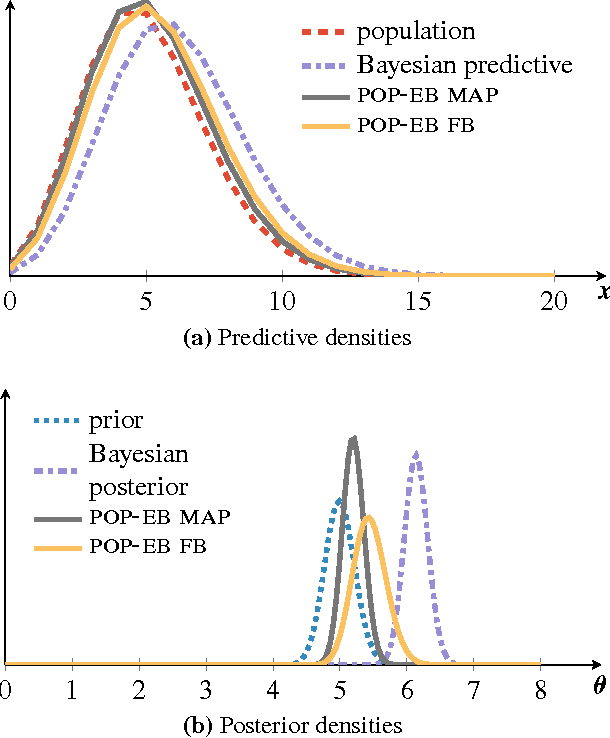
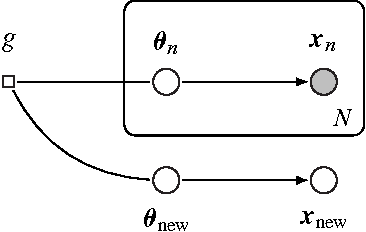
Bayesian predictive inference analyzes a dataset to make predictions about new observations. When a model does not match the data, predictive accuracy suffers. We develop population empirical Bayes (POP-EB), a hierarchical framework that explicitly models the empirical population distribution as part of Bayesian analysis. We introduce a new concept, the latent dataset, as a hierarchical variable and set the empirical population as its prior. This leads to a new predictive density that mitigates model mismatch. We efficiently apply this method to complex models by proposing a stochastic variational inference algorithm, called bumping variational inference (BUMP-VI). We demonstrate improved predictive accuracy over classical Bayesian inference in three models: a linear regression model of health data, a Bayesian mixture model of natural images, and a latent Dirichlet allocation topic model of scientific documents.