Hindsight Expectation Maximization for Goal-conditioned Reinforcement Learning
Paper and Code
Jun 13, 2020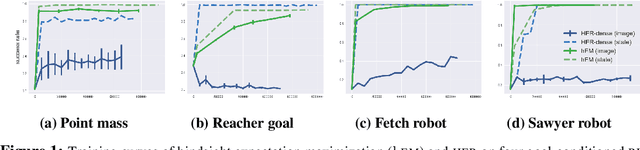
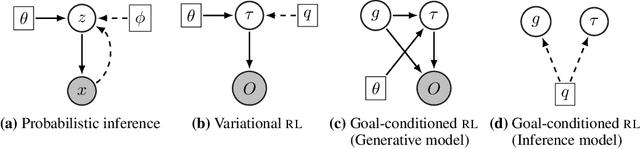
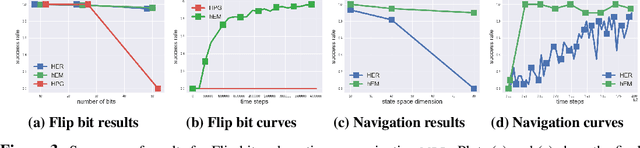
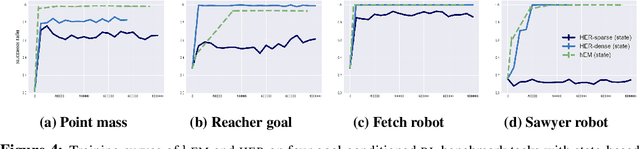
We propose a graphical model framework for goal-conditioned RL, with an EM algorithm that operates on the lower bound of the RL objective. The E-step provides a natural interpretation of how 'learning in hindsight' techniques, such as HER, to handle extremely sparse goal-conditioned rewards. The M-step reduces policy optimization to supervised learning updates, which greatly stabilizes end-to-end training on high-dimensional inputs such as images. We show that the combined algorithm, hEM significantly outperforms model-free baselines on a wide range of goal-conditioned benchmarks with sparse rewards.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge